
- SciPy 教程
- SciPy - 首頁
- SciPy - 簡介
- SciPy - 環境設定
- SciPy - 基本功能
- SciPy - 聚類分析
- SciPy - 常量
- SciPy - FFTpack (快速傅立葉變換)
- SciPy - Integrate (積分)
- SciPy - Interpolate (插值)
- SciPy - 輸入和輸出
- SciPy - Linalg (線性代數)
- SciPy - Ndimage (多維影像)
- SciPy - Optimize (最佳化)
- SciPy - Stats (統計)
- SciPy - CSGraph (壓縮稀疏圖)
- SciPy - Spatial (空間資料)
- SciPy - ODR (正交距離迴歸)
- SciPy - Special Package (特殊函式包)
- SciPy 有用資源
- SciPy - 參考
- SciPy 快速指南
- SciPy - 有用資源
- SciPy - 討論
SciPy 快速指南
SciPy - 簡介
SciPy,讀作“Sigh Pi”,是一個基於Python的開源科學計算庫,根據BSD許可證釋出,用於執行數學、科學和工程計算。
SciPy 庫依賴於 NumPy,NumPy 提供了方便快捷的 N 維陣列操作。SciPy 庫構建在 NumPy 陣列之上,並提供了許多使用者友好且高效的數值計算方法,例如數值積分和最佳化的例程。它們都可以在所有流行的作業系統上執行,安裝快速且免費。NumPy 和 SciPy 易於使用,但功能強大,足以被世界上一些領先的科學家和工程師所依賴。
SciPy 子包
SciPy 被組織成涵蓋不同科學計算領域的子包。這些子包在下面的表格中進行了總結:
| scipy.cluster | 向量量化/K均值聚類 |
| scipy.constants | 物理和數學常數 |
| scipy.fftpack | 傅立葉變換 |
| scipy.integrate | 積分例程 |
| scipy.interpolate | 插值 |
| scipy.io | 資料輸入和輸出 |
| scipy.linalg | 線性代數例程 |
| scipy.ndimage | N 維影像包 |
| scipy.odr | 正交距離迴歸 |
| scipy.optimize | 最佳化 |
| scipy.signal | 訊號處理 |
| scipy.sparse | 稀疏矩陣 |
| scipy.spatial | 空間資料結構和演算法 |
| scipy.special | 各種特殊數學函式 |
| scipy.stats | 統計 |
資料結構
SciPy 使用的基本資料結構是由 NumPy 模組提供的多維陣列。NumPy 提供了一些用於線性代數、傅立葉變換和隨機數生成的函式,但其通用性不如 SciPy 中的等效函式。
SciPy - 環境設定
標準 Python 發行版不包含任何 SciPy 模組。一種輕量級的替代方法是使用流行的 Python 包安裝程式安裝 SciPy,
pip install pandas
如果我們安裝了**Anaconda Python 包**,Pandas 將預設安裝。以下是不同作業系統中安裝它們的軟體包和連結。
Windows
**Anaconda**(來自 https://www.continuum.io)是 SciPy 棧的免費 Python 發行版。它也適用於 Linux 和 Mac。
**Canopy** (https://www.enthought.com/products/canopy/) 提供免費版和商業版,其中包含適用於 Windows、Linux 和 Mac 的完整 SciPy 棧。
**Python(x,y)** - 這是一個帶有 SciPy 棧和 Spyder IDE 的免費 Python 發行版,適用於 Windows 作業系統。(可從 https://python-xy.github.io/ 下載)
Linux
使用各個 Linux 發行版的包管理器來安裝 SciPy 棧中的一個或多個包。
Ubuntu
我們可以使用以下路徑在 Ubuntu 中安裝 Python。
sudo apt-get install python-numpy python-scipy python-matplotlibipythonipython-notebook python-pandas python-sympy python-nose
Fedora
我們可以使用以下路徑在 Fedora 中安裝 Python。
sudo yum install numpyscipy python-matplotlibipython python-pandas sympy python-nose atlas-devel
SciPy - 基本功能
預設情況下,所有 NumPy 函式都可透過 SciPy 名稱空間訪問。匯入 SciPy 後,無需顯式匯入 NumPy 函式。NumPy 的主要物件是同質多維陣列。它是一個元素(通常是數字)表,所有元素型別相同,由正整數元組索引。在 NumPy 中,維度稱為軸。軸的數量稱為秩。
現在,讓我們回顧一下 NumPy 中向量和矩陣的基本功能。由於 SciPy 建立在 NumPy 陣列之上,因此瞭解 NumPy 基礎知識是必要的,因為線性代數的大部分內容都只處理矩陣。
NumPy 向量
向量可以透過多種方式建立。下面描述其中一些方法。
將 Python 類陣列物件轉換為 NumPy 陣列
讓我們考慮以下示例。
import numpy as np list = [1,2,3,4] arr = np.array(list) print arr
上述程式的輸出如下所示。
[1 2 3 4]
NumPy 本身的陣列建立
NumPy 具有從頭開始建立陣列的內建函式。下面解釋其中一些函式。
使用 zeros()
zeros(shape) 函式將建立一個用 0 值填充的陣列,其形狀由引數指定。預設 dtype 為 float64。讓我們考慮以下示例。
import numpy as np print np.zeros((2, 3))
上述程式的輸出如下所示。
array([[ 0., 0., 0.], [ 0., 0., 0.]])
使用 ones()
ones(shape) 函式將建立一個用 1 值填充的陣列。在其他方面與 zeros 相同。讓我們考慮以下示例。
import numpy as np print np.ones((2, 3))
上述程式的輸出如下所示。
array([[ 1., 1., 1.], [ 1., 1., 1.]])
使用 arange()
arange() 函式將建立具有規律遞增值的陣列。讓我們考慮以下示例。
import numpy as np print np.arange(7)
上述程式將生成以下輸出。
array([0, 1, 2, 3, 4, 5, 6])
定義值的 資料型別
讓我們考慮以下示例。
import numpy as np arr = np.arange(2, 10, dtype = np.float) print arr print "Array Data Type :",arr.dtype
上述程式將生成以下輸出。
[ 2. 3. 4. 5. 6. 7. 8. 9.] Array Data Type : float64
使用 linspace()
linspace() 函式將建立具有指定數量元素的陣列,這些元素將均勻地分佈在指定的起始值和結束值之間。讓我們考慮以下示例。
import numpy as np print np.linspace(1., 4., 6)
上述程式將生成以下輸出。
array([ 1. , 1.6, 2.2, 2.8, 3.4, 4. ])
矩陣
矩陣是一個特殊的二維陣列,它在運算過程中保持其二維特性。它具有一些特殊的運算子,例如 *(矩陣乘法)和 **(矩陣冪)。讓我們考慮以下示例。
import numpy as np
print np.matrix('1 2; 3 4')
上述程式將生成以下輸出。
matrix([[1, 2], [3, 4]])
矩陣的共軛轉置
此功能返回 `self` 的(複數)共軛轉置。讓我們考慮以下示例。
import numpy as np
mat = np.matrix('1 2; 3 4')
print mat.H
上述程式將生成以下輸出。
matrix([[1, 3],
[2, 4]])
矩陣的轉置
此功能返回 `self` 的轉置。讓我們考慮以下示例。
import numpy as np
mat = np.matrix('1 2; 3 4')
mat.T
上述程式將生成以下輸出。
matrix([[1, 3],
[2, 4]])
當我們轉置矩陣時,我們建立一個新的矩陣,其行是原始矩陣的列。另一方面,共軛轉置為每個矩陣元素交換行和列索引。矩陣的逆矩陣是一個矩陣,如果它與原始矩陣相乘,則結果為單位矩陣。
SciPy - 聚類分析
**K 均值聚類**是一種在未標記資料集中查詢聚類和聚類中心的方法。直觀地說,我們可能會將一個聚類理解為——由一組資料點組成,其點與點之間的距離與到聚類外部點的距離相比很小。給定一組初始的 K 箇中心,K 均值演算法迭代以下兩個步驟:
對於每個中心,識別比任何其他中心都更靠近它的訓練點子集(其聚類)。
計算每個聚類中資料點每個特徵的均值,該均值向量成為該聚類的新的中心。
這兩個步驟重複進行,直到中心不再移動或分配不再改變。然後,可以將新點**x**分配到最接近原型的聚類。SciPy 庫透過 cluster 包提供了一個很好的 K 均值演算法實現。讓我們瞭解如何使用它。
SciPy 中的 K 均值實現
我們將瞭解如何在 SciPy 中實現 K 均值。
匯入 K 均值
我們將看到每個匯入函式的實現和用法。
from SciPy.cluster.vq import kmeans,vq,whiten
資料生成
我們必須模擬一些資料來探索聚類。
from numpy import vstack,array from numpy.random import rand # data generation with three features data = vstack((rand(100,3) + array([.5,.5,.5]),rand(100,3)))
現在,我們必須檢查資料。上述程式將生成以下輸出。
array([[ 1.48598868e+00, 8.17445796e-01, 1.00834051e+00],
[ 8.45299768e-01, 1.35450732e+00, 8.66323621e-01],
[ 1.27725864e+00, 1.00622682e+00, 8.43735610e-01],
…………….
按特徵基礎對一組觀察值進行歸一化。在執行 K 均值之前,最好使用白化重新縮放觀察集的每個特徵維度。每個特徵除以其在所有觀察值中的標準差,使其方差為單位。
對資料進行白化處理
我們必須使用以下程式碼對資料進行白化處理。
# whitening of data data = whiten(data)
使用三個聚類計算 K 均值
現在,讓我們使用以下程式碼使用三個聚類計算 K 均值。
# computing K-Means with K = 3 (2 clusters) centroids,_ = kmeans(data,3)
上述程式碼對形成 K 個聚類的一組觀察向量執行 K 均值。K 均值演算法調整質心,直到無法取得足夠的進展,即自上次迭代以來失真變化小於某個閾值。在這裡,我們可以透過使用下面給出的程式碼列印 centroids 變數來觀察聚類的質心。
print(centroids)
上述程式碼將生成以下輸出。
print(centroids)[ [ 2.26034702 1.43924335 1.3697022 ]
[ 2.63788572 2.81446462 2.85163854]
[ 0.73507256 1.30801855 1.44477558] ]
使用下面給出的程式碼將每個值分配給一個聚類。
# assign each sample to a cluster clx,_ = vq(data,centroids)
**vq** 函式將 `M` x `N` 的 **obs** 陣列中的每個觀察向量與質心進行比較,並將觀察值分配給最接近的聚類。它返回每個觀察值的聚類和失真。我們也可以檢查失真。讓我們使用以下程式碼檢查每個觀察值的聚類。
# check clusters of observation print clx
上述程式碼將生成以下輸出。
array([1, 1, 0, 1, 1, 1, 0, 1, 0, 0, 1, 1, 1, 0, 0, 1, 1, 0, 0, 1, 0, 2, 0, 2, 0, 1, 1, 1, 0, 0, 1, 1, 0, 0, 1, 1, 0, 0, 0, 0, 1, 1, 0, 0, 1, 1, 0, 0, 1, 0, 1, 0, 0, 0, 1, 1, 0, 0, 0, 1, 0, 1, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 1, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1, 0, 0, 1, 2, 1, 2, 2, 2, 2, 2, 2, 2, 2, 0, 2, 0, 2, 2, 2, 2, 2, 0, 0, 2, 2, 2, 1, 0, 2, 0, 2, 2, 2, 2, 2, 2, 2, 2, 2, 0, 2, 2, 1, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 0, 2, 0, 2, 2, 2, 2, 2, 2, 2, 2, 2, 0, 2, 2, 2, 2, 0, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 1, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2], dtype=int32)
上述陣列的不同值 0、1、2 表示聚類。
SciPy - 常量
SciPy 常量包提供了廣泛的常數,這些常數用於一般的科學領域。
SciPy 常量包
**scipy.constants 包**提供了各種常數。我們必須匯入所需的常數並根據需要使用它們。讓我們看看這些常量變數是如何匯入和使用的。
首先,讓我們透過考慮以下示例來比較 'pi' 值。
#Import pi constant from both the packages
from scipy.constants import pi
from math import pi
print("sciPy - pi = %.16f"%scipy.constants.pi)
print("math - pi = %.16f"%math.pi)
上述程式將生成以下輸出。
sciPy - pi = 3.1415926535897931 math - pi = 3.1415926535897931
可用常量列表
下表簡要描述了各種常數。
數學常數
| 序號 | 常量 | 描述 |
|---|---|---|
| 1 | pi | pi |
| 2 | golden | 黃金比例 |
物理常數
下表列出了最常用的物理常數。
| 序號 | 常量和描述 |
|---|---|
| 1 | c 真空中的光速 |
| 2 | speed_of_light 真空中的光速 |
| 3 | h 普朗克常數 |
| 4 | Planck 普朗克常數 h |
| 5 | G 牛頓引力常數 |
| 6 | e 元電荷 |
| 7 | R 摩爾氣體常數 |
| 8 | Avogadro 阿伏伽德羅常數 |
| 9 | k 玻爾茲曼常數 |
| 10 | electron_mass (或) m_e 電子質量 |
| 11 | proton_mass (或) m_p 質子質量 |
| 12 | neutron_mass (或) m_n 中子質量 |
單位
下表列出了 SI 單位。
| 序號 | 單位 | 值 |
|---|---|---|
| 1 | milli (毫) | 0.001 |
| 2 | micro (微) | 1e-06 |
| 3 | kilo (千) | 1000 |
這些單位範圍從堯、澤、艾、拍、太……千、百……納、皮……到仄。
其他重要常數
下表列出了 SciPy 中使用的其他重要常數。
| 序號 | 單位 | 值 |
|---|---|---|
| 1 | gram (克) | 0.001 kg |
| 2 | atomic mass (原子質量) | 原子質量常數 |
| 3 | degree (度) | 度(弧度) |
| 4 | minute (分) | 一分(秒) |
| 5 | day (天) | 一天(秒) |
| 6 | inch (英寸) | 一英寸(米) |
| 7 | micron (微米) | 一微米(米) |
| 8 | light_year (光年) | 一光年(米) |
| 9 | atm (標準大氣壓) | 標準大氣壓(帕斯卡) |
| 10 | acre (英畝) | 一英畝(平方米) |
| 11 | liter (升) | 一升(立方米) |
| 12 | gallon (加侖) | 一加侖(立方米) |
| 13 | kmh (千米每小時) | 千米每小時(米每秒) |
| 14 | degree_Fahrenheit (華氏度) | 一度華氏(開爾文) |
| 15 | eV (電子伏特) | 一電子伏特(焦耳) |
| 16 | hp (馬力) | 一馬力(瓦特) |
| 17 | dyn (達因) | 一達因(牛頓) |
| 18 | lambda2nu | 將波長轉換為光學頻率 |
記住所有這些有點困難。獲取哪個鍵對應哪個函式的簡單方法是使用 **scipy.constants.find()** 方法。讓我們考慮以下示例。
import scipy.constants res = scipy.constants.physical_constants["alpha particle mass"] print res
上述程式將生成以下輸出。
[ 'alpha particle mass', 'alpha particle mass energy equivalent', 'alpha particle mass energy equivalent in MeV', 'alpha particle mass in u', 'electron to alpha particle mass ratio' ]
此方法返回鍵列表,如果關鍵字不匹配則返回空。
SciPy - FFTpack (快速傅立葉變換)
傅立葉變換用於計算時域訊號,以檢查其在頻域中的行為。傅立葉變換廣泛應用於訊號和噪聲處理、影像處理、音訊訊號處理等領域。SciPy 提供了 fftpack 模組,允許使用者計算快速傅立葉變換。
下面是一個正弦函式的例子,我們將使用 fftpack 模組計算其傅立葉變換。
快速傅立葉變換
讓我們詳細瞭解什麼是快速傅立葉變換。
一維離散傅立葉變換
長度為 N 的序列 x[n] 的長度為 N 的 FFT y[k] 由 fft() 計算,逆變換由 ifft() 計算。讓我們考慮以下示例
#Importing the fft and inverse fft functions from fftpackage from scipy.fftpack import fft #create an array with random n numbers x = np.array([1.0, 2.0, 1.0, -1.0, 1.5]) #Applying the fft function y = fft(x) print y
上述程式將生成以下輸出。
[ 4.50000000+0.j 2.08155948-1.65109876j -1.83155948+1.60822041j -1.83155948-1.60822041j 2.08155948+1.65109876j ]
讓我們看另一個例子
#FFT is already in the workspace, using the same workspace to for inverse transform yinv = ifft(y) print yinv
上述程式將生成以下輸出。
[ 1.0+0.j 2.0+0.j 1.0+0.j -1.0+0.j 1.5+0.j ]
scipy.fftpack 模組允許計算快速傅立葉變換。作為一個例子,一個(含噪聲的)輸入訊號可能如下所示:
import numpy as np time_step = 0.02 period = 5. time_vec = np.arange(0, 20, time_step) sig = np.sin(2 * np.pi / period * time_vec) + 0.5 *np.random.randn(time_vec.size) print sig.size
我們正在建立一個時間步長為 0.02 秒的訊號。最後一條語句列印訊號 sig 的大小。輸出如下:
1000
我們不知道訊號頻率;我們只知道訊號 sig 的取樣時間步長。該訊號應該來自一個實函式,因此傅立葉變換將是對稱的。scipy.fftpack.fftfreq() 函式將生成取樣頻率,而 scipy.fftpack.fft() 將計算快速傅立葉變換。
讓我們透過一個例子來理解這一點。
from scipy import fftpack sample_freq = fftpack.fftfreq(sig.size, d = time_step) sig_fft = fftpack.fft(sig) print sig_fft
上述程式將生成以下輸出。
array([ 25.45122234 +0.00000000e+00j, 6.29800973 +2.20269471e+00j, 11.52137858 -2.00515732e+01j, 1.08111300 +1.35488579e+01j, …….])
離散餘弦變換
離散餘弦變換 (DCT) 將有限的資料點序列表示為不同頻率振盪的餘弦函式之和。SciPy 使用函式 dct 提供 DCT,並使用函式 idct 提供相應的 IDCT。讓我們考慮以下示例。
from scipy.fftpack import dct print dct(np.array([4., 3., 5., 10., 5., 3.]))
上述程式將生成以下輸出。
array([ 60., -3.48476592, -13.85640646, 11.3137085, 6., -6.31319305])
逆離散餘弦變換根據其離散餘弦變換 (DCT) 係數重建序列。idct 函式是 dct 函式的逆函式。讓我們透過以下示例來理解這一點。
from scipy.fftpack import dct print idct(np.array([4., 3., 5., 10., 5., 3.]))
上述程式將生成以下輸出。
array([ 39.15085889, -20.14213562, -6.45392043, 7.13341236, 8.14213562, -3.83035081])
SciPy - Integrate (積分)
當一個函式無法解析地積分,或者解析地積分非常困難時,通常會轉向數值積分方法。SciPy 有許多用於執行數值積分的例程。它們大部分都位於相同的 scipy.integrate 庫中。下表列出了一些常用的函式。
| 序號 | 函式及描述 |
|---|---|
| 1 | quad 單重積分 |
| 2 | dblquad 二重積分 |
| 3 | tplquad 三重積分 |
| 4 | nquad n 重多重積分 |
| 5 | fixed_quad 高斯求積,n 階 |
| 6 | quadrature 高斯求積到容差 |
| 7 | romberg 龍貝格積分 |
| 8 | trapz 梯形法則 |
| 9 | cumtrapz 梯形法則累積計算積分 |
| 10 | simps 辛普森法則 |
| 11 | romb 龍貝格積分 |
| 12 | polyint 解析多項式積分 (NumPy) |
| 13 | poly1d polyint 的輔助函式 (NumPy) |
單重積分
Quad 函式是 SciPy 積分函式的核心。數值積分有時稱為求積,因此得名。它通常是執行函式 *f(x)* 在從 a 到 b 的給定固定範圍內的單重積分的預設選擇。
$$\int_{a}^{b} f(x)dx$$
quad 的一般形式是 scipy.integrate.quad(f, a, b),其中“f”是要積分的函式的名稱。“a”和“b”分別是下限和上限。讓我們看一個高斯函式在 0 和 1 範圍內的積分示例。
我們首先需要定義函式 → $f(x) = e^{-x^2}$,這可以使用 lambda 表示式完成,然後在該函式上呼叫 quad 方法。
import scipy.integrate from numpy import exp f= lambda x:exp(-x**2) i = scipy.integrate.quad(f, 0, 1) print i
上述程式將生成以下輸出。
(0.7468241328124271, 8.291413475940725e-15)
quad 函式返回兩個值,其中第一個數字是積分值,第二個值是積分值絕對誤差的估計值。
注意 - 由於 quad 需要函式作為第一個引數,因此我們不能直接將 exp 作為引數傳遞。Quad 函式接受正無窮大和負無窮大作為極限。Quad 函式可以積分單個變數的標準預定義 NumPy 函式,例如 exp、sin 和 cos。
多重積分
二重積分和三重積分的機制已被封裝到 dblquad、tplquad 和 nquad 函式中。這些函式分別整合四個或六個引數。所有內積分的極限都需要定義為函式。
二重積分
dblquad 的一般形式為 scipy.integrate.dblquad(func, a, b, gfun, hfun)。其中,func 是要積分的函式的名稱,“a”和“b”分別是 x 變數的下限和上限,而 gfun 和 hfun 是定義 y 變數的下限和上限的函式的名稱。
例如,讓我們執行二重積分方法。
$$\int_{0}^{1/2} dy \int_{0}^{\sqrt{1-4y^2}} 16xy \:dx$$
我們使用 lambda 表示式定義函式 f、g 和 h。請注意,即使 g 和 h 是常數,就像在許多情況下一樣,它們也必須定義為函式,就像我們這裡為下限所做的那樣。
import scipy.integrate from numpy import exp from math import sqrt f = lambda x, y : 16*x*y g = lambda x : 0 h = lambda y : sqrt(1-4*y**2) i = scipy.integrate.dblquad(f, 0, 0.5, g, h) print i
上述程式將生成以下輸出。
(0.5, 1.7092350012594845e-14)
除了上面描述的例程之外,scipy.integrate 還有一些其他的積分例程,包括 nquad,它執行 n 重多重積分,以及實現各種積分演算法的其他例程。但是,quad 和 dblquad 將滿足我們對數值積分的大部分需求。
SciPy - Interpolate (插值)
在本章中,我們將討論插值如何在 SciPy 中發揮作用。
什麼是插值?
插值是線上或曲線上的兩點之間查詢值的過程。為了幫助我們記住它的含義,我們應該將單詞的第一部分“inter”理解為“進入”,這提醒我們要檢視我們最初擁有的資料的“內部”。插值這個工具不僅在統計學中很有用,而且在科學、商業或需要預測落入兩個現有資料點之間的值時也很有用。
讓我們建立一些資料,看看如何使用 scipy.interpolate 包進行此插值。
import numpy as np from scipy import interpolate import matplotlib.pyplot as plt x = np.linspace(0, 4, 12) y = np.cos(x**2/3+4) print x,y
上述程式將生成以下輸出。
(
array([0., 0.36363636, 0.72727273, 1.09090909, 1.45454545, 1.81818182,
2.18181818, 2.54545455, 2.90909091, 3.27272727, 3.63636364, 4.]),
array([-0.65364362, -0.61966189, -0.51077021, -0.31047698, -0.00715476,
0.37976236, 0.76715099, 0.99239518, 0.85886263, 0.27994201,
-0.52586509, -0.99582185])
)
現在,我們有兩個陣列。假設這兩個陣列是空間中點的兩個維度,讓我們使用以下程式進行繪圖,看看它們是什麼樣的。
plt.plot(x, y,’o’) plt.show()
上述程式將生成以下輸出。
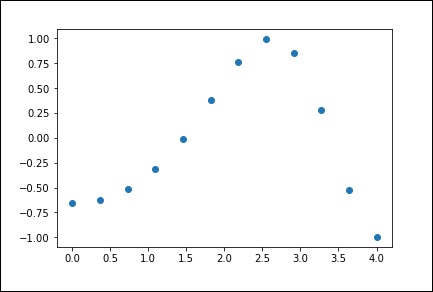
一維插值
scipy.interpolate 中的 interp1d 類是一種方便的方法,可以根據固定的資料點建立函式,可以使用線性插值在給定資料定義的域內的任何位置進行評估。
使用以上資料,讓我們建立一個插值函式並繪製一個新的插值圖。
f1 = interp1d(x, y,kind = 'linear') f2 = interp1d(x, y, kind = 'cubic')
使用 interp1d 函式,我們建立了兩個函式 f1 和 f2。這些函式對於給定的輸入 x 返回 y。第三個變數 kind 表示插值技術的型別。“線性”、“最近鄰”、“零”、“Slinear”、“二次”、“三次”是幾種插值技術。
現在,讓我們建立一個新的更長輸入,以檢視插值的明顯差異。我們將對新資料使用舊資料的相同函式。
xnew = np.linspace(0, 4,30) plt.plot(x, y, 'o', xnew, f(xnew), '-', xnew, f2(xnew), '--') plt.legend(['data', 'linear', 'cubic','nearest'], loc = 'best') plt.show()
上述程式將生成以下輸出。
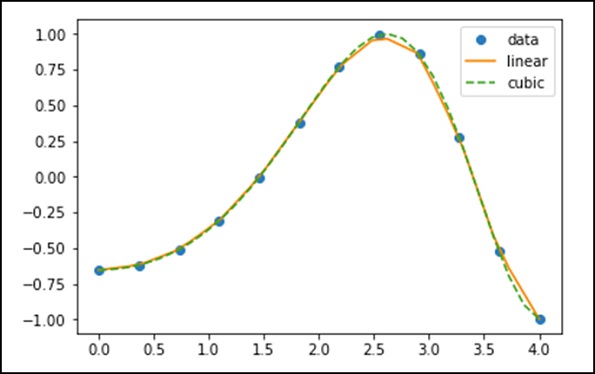
樣條曲線
為了繪製穿過資料點的平滑曲線,繪圖員曾經使用過稱為機械樣條曲線的薄而靈活的木條、硬橡膠、金屬或塑膠條。要使用機械樣條曲線,需要將大頭針放置在設計曲線上的明智選擇的點上,然後彎曲樣條曲線,使其接觸到這些大頭針中的每一個。
顯然,透過這種構造,樣條曲線在這些大頭針處對曲線進行插值。它可用於在其他圖紙中複製曲線。放置大頭針的點稱為節點。我們可以透過調整節點的位置來改變樣條曲線定義的曲線的形狀。
單變數樣條曲線
一維平滑樣條曲線擬合給定的資料集。scipy.interpolate 中的 UnivariateSpline 類是一種方便的方法,可以根據固定的資料點建立函式類 – scipy.interpolate.UnivariateSpline(x, y, w = None, bbox = [None, None], k = 3, s = None, ext = 0, check_finite = False)。
引數 - 下面是單變數樣條曲線的引數。
這將 k 次樣條曲線 y = spl(x) 擬合到提供的 x、y 資料。
‘w’ - 指定樣條擬合的權重。必須為正。如果沒有(預設值),則所有權重都相等。
‘s’ - 透過指定平滑條件來指定節點數。
‘k’ - 平滑樣條的次數。必須 <= 5。預設為 k = 3,三次樣條曲線。
Ext - 控制不在節點序列定義的區間內的元素的外推模式。
如果 ext = 0 或 'extrapolate',則返回外推值。
如果 ext = 1 或 'zero',則返回 0
如果 ext = 2 或 'raise',則引發 ValueError
如果 ext = 3 或 'const',則返回邊界值。
check_finite – 是否檢查輸入陣列僅包含有限數字。
讓我們考慮以下示例。
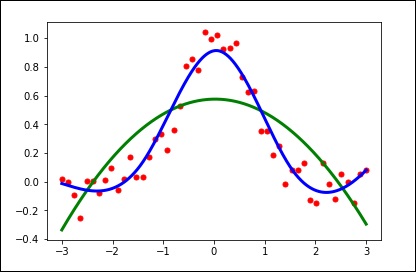
import matplotlib.pyplot as plt from scipy.interpolate import UnivariateSpline x = np.linspace(-3, 3, 50) y = np.exp(-x**2) + 0.1 * np.random.randn(50) plt.plot(x, y, 'ro', ms = 5) plt.show()
使用平滑引數的預設值。
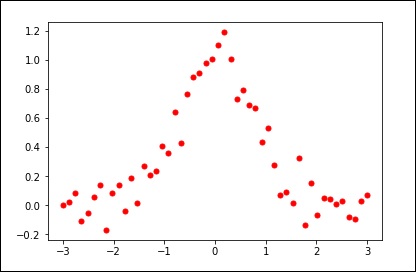
spl = UnivariateSpline(x, y) xs = np.linspace(-3, 3, 1000) plt.plot(xs, spl(xs), 'g', lw = 3) plt.show()
手動更改平滑量。
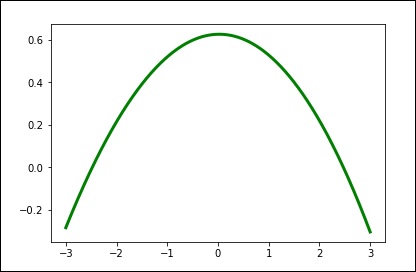
spl.set_smoothing_factor(0.5) plt.plot(xs, spl(xs), 'b', lw = 3) plt.show()
SciPy - 輸入和輸出
Scipy.io(輸入和輸出)包提供了廣泛的功能,可以處理不同格式的檔案。其中一些格式是:
- MATLAB
- IDL
- 矩陣市場
- Wave
- Arff
- Netcdf 等。
讓我們詳細討論最常用的檔案格式:
MATLAB
以下是用於載入和儲存 .mat 檔案的函式。
| 序號 | 函式及描述 |
|---|---|
| 1 | loadmat 載入 MATLAB 檔案 |
| 2 | savemat 儲存 MATLAB 檔案 |
| 3 | whosmat 列出 MATLAB 檔案中的變數 |
讓我們考慮以下示例。
import scipy.io as sio
import numpy as np
#Save a mat file
vect = np.arange(10)
sio.savemat('array.mat', {'vect':vect})
#Now Load the File
mat_file_content = sio.loadmat(‘array.mat’)
Print mat_file_content
上述程式將生成以下輸出。
{
'vect': array([[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]]), '__version__': '1.0',
'__header__': 'MATLAB 5.0 MAT-file Platform: posix, Created on: Sat Sep 30
09:49:32 2017', '__globals__': []
}
我們可以看到包含元資訊的陣列。如果我們想在不將資料讀入記憶體的情況下檢查 MATLAB 檔案的內容,請使用如下所示的 whosmat 命令。
import scipy.io as sio mat_file_content = sio.whosmat(‘array.mat’) print mat_file_content
上述程式將生成以下輸出。
[('vect', (1, 10), 'int64')]
SciPy - Linalg (線性代數)
SciPy 使用最佳化的 ATLAS LAPACK 和 BLAS 庫構建。它具有非常快速的線性代數能力。所有這些線性代數例程都期望一個可以轉換為二維陣列的物件。這些例程的輸出也是二維陣列。
SciPy.linalg 與 NumPy.linalg 的比較
scipy.linalg 包含 numpy.linalg 中的所有函式。此外,scipy.linalg 還有一些 numpy.linalg 中沒有的其他高階函式。與 numpy.linalg 相比,使用 scipy.linalg 的另一個優點是它始終與 BLAS/LAPACK 支援一起編譯,而對於 NumPy,這是可選的。因此,SciPy 版本的速度可能更快,具體取決於 NumPy 的安裝方式。
線性方程
scipy.linalg.solve 功能求解線性方程 a * x + b * y = Z,以求解未知的 x、y 值。
例如,假設需要求解以下聯立方程。
x + 3y + 5z = 10
2x + 5y + z = 8
2x + 3y + 8z = 3
為了求解上述方程組中的 x、y、z 值,我們可以使用矩陣求逆法找到解向量,如下所示。
$$
但是,最好使用linalg.solve命令,因為它速度更快,數值穩定性也更好。
solve 函式接受兩個輸入 ‘a’ 和 ‘b’,其中 ‘a’ 表示係數,‘b’ 表示右側的值,並返回解陣列。
讓我們考慮以下示例。
#importing the scipy and numpy packages from scipy import linalg import numpy as np #Declaring the numpy arrays a = np.array([[3, 2, 0], [1, -1, 0], [0, 5, 1]]) b = np.array([2, 4, -1]) #Passing the values to the solve function x = linalg.solve(a, b) #printing the result array print x
上述程式將生成以下輸出。
array([ 2., -2., 9.])
求解行列式
方陣 A 的行列式通常表示為 |A|,它是線性代數中經常使用的量。在 SciPy 中,可以使用det()函式計算它。它接收一個矩陣作為輸入,並返回一個標量值。
讓我們考慮以下示例。
#importing the scipy and numpy packages from scipy import linalg import numpy as np #Declaring the numpy array A = np.array([[1,2],[3,4]]) #Passing the values to the det function x = linalg.det(A) #printing the result print x
上述程式將生成以下輸出。
-2.0
特徵值和特徵向量
特徵值-特徵向量問題是最常用的線性代數運算之一。我們可以透過考慮以下關係式來找到方陣 (A) 的特徵值 (λ) 和相應的特徵向量 (v):
Av = λv
scipy.linalg.eig計算普通或廣義特徵值問題的特徵值。此函式返回特徵值和特徵向量。
讓我們考慮以下示例。
#importing the scipy and numpy packages from scipy import linalg import numpy as np #Declaring the numpy array A = np.array([[1,2],[3,4]]) #Passing the values to the eig function l, v = linalg.eig(A) #printing the result for eigen values print l #printing the result for eigen vectors print v
上述程式將生成以下輸出。
array([-0.37228132+0.j, 5.37228132+0.j]) #--Eigen Values
array([[-0.82456484, -0.41597356], #--Eigen Vectors
[ 0.56576746, -0.90937671]])
奇異值分解
奇異值分解 (SVD) 可以被認為是特徵值問題到非方陣矩陣的擴充套件。
scipy.linalg.svd將矩陣 ‘a’ 分解為兩個酉矩陣 ‘U’ 和 ‘Vh’ 以及一個包含奇異值(實數,非負)的一維陣列 ‘s’,使得 a == U*S*Vh,其中 ‘S’ 是一個形狀合適的矩陣,其主對角線為 ‘s’,其餘元素為零。
讓我們考慮以下示例。
#importing the scipy and numpy packages from scipy import linalg import numpy as np #Declaring the numpy array a = np.random.randn(3, 2) + 1.j*np.random.randn(3, 2) #Passing the values to the eig function U, s, Vh = linalg.svd(a) # printing the result print U, Vh, s
上述程式將生成以下輸出。
(
array([
[ 0.54828424-0.23329795j, -0.38465728+0.01566714j,
-0.18764355+0.67936712j],
[-0.27123194-0.5327436j , -0.57080163-0.00266155j,
-0.39868941-0.39729416j],
[ 0.34443818+0.4110186j , -0.47972716+0.54390586j,
0.25028608-0.35186815j]
]),
array([ 3.25745379, 1.16150607]),
array([
[-0.35312444+0.j , 0.32400401+0.87768134j],
[-0.93557636+0.j , -0.12229224-0.33127251j]
])
)
SciPy - Ndimage (多維影像)
SciPy 的 ndimage 子模組專門用於影像處理。這裡,ndimage 指的是 n 維影像。
影像處理中最常見的一些任務如下:
- 輸入/輸出,顯示影像
- 基本操作——裁剪、翻轉、旋轉等。
- 影像濾波——去噪、銳化等。
- 影像分割——標記對應於不同物件的畫素
- 分類
- 特徵提取
- 配準
讓我們討論如何使用 SciPy 實現其中一些任務。
開啟和寫入影像檔案
SciPy 中的misc 包包含一些影像。我們使用這些影像來學習影像處理操作。讓我們考慮以下示例。
from scipy import misc
f = misc.face()
misc.imsave('face.png', f) # uses the Image module (PIL)
import matplotlib.pyplot as plt
plt.imshow(f)
plt.show()
上述程式將生成以下輸出。

任何原始格式的影像都是矩陣格式中數字表示的顏色的組合。機器僅根據這些數字來理解和處理影像。RGB 是一種流行的表示方式。
讓我們看看上面影像的統計資訊。
from scipy import misc face = misc.face(gray = False) print face.mean(), face.max(), face.min()
上述程式將生成以下輸出。
110.16274388631184, 255, 0
現在,我們知道影像是由數字構成的,因此數字值的任何變化都會改變原始影像。讓我們對影像執行一些幾何變換。基本幾何操作是裁剪。
from scipy import misc face = misc.face(gray = True) lx, ly = face.shape # Cropping crop_face = face[lx / 4: - lx / 4, ly / 4: - ly / 4] import matplotlib.pyplot as plt plt.imshow(crop_face) plt.show()
上述程式將生成以下輸出。

我們還可以執行一些基本操作,例如將影像倒置,如下所示。
# up <-> down flip from scipy import misc face = misc.face() flip_ud_face = np.flipud(face) import matplotlib.pyplot as plt plt.imshow(flip_ud_face) plt.show()
上述程式將生成以下輸出。

除此之外,我們還有rotate()函式,它可以將影像旋轉指定的角度。
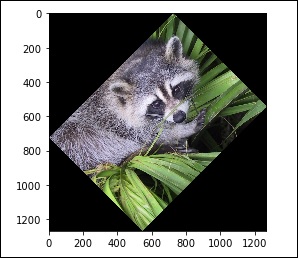
# rotation from scipy import misc,ndimage face = misc.face() rotate_face = ndimage.rotate(face, 45) import matplotlib.pyplot as plt plt.imshow(rotate_face) plt.show()
上述程式將生成以下輸出。
濾波器
讓我們討論濾波器如何幫助影像處理。
什麼是影像處理中的濾波?
濾波是一種修改或增強影像的技術。例如,您可以濾波影像以強調某些特徵或去除其他特徵。使用濾波實現的影像處理操作包括平滑、銳化和邊緣增強。
濾波是一種鄰域運算,其中輸出影像中任何給定畫素的值是透過對相應輸入畫素鄰域中的畫素值應用某種演算法來確定的。現在讓我們使用 SciPy ndimage 執行一些操作。
模糊
模糊廣泛用於減少影像中的噪聲。我們可以執行濾波操作並檢視影像的變化。讓我們考慮以下示例。
from scipy import misc face = misc.face() blurred_face = ndimage.gaussian_filter(face, sigma=3) import matplotlib.pyplot as plt plt.imshow(blurred_face) plt.show()
上述程式將生成以下輸出。

sigma 值表示五級模糊程度。我們可以透過調整 sigma 值來檢視影像質量的變化。有關模糊的更多詳細資訊,請點選 → DIP(數字影像處理)教程。
邊緣檢測
讓我們討論邊緣檢測如何幫助影像處理。
什麼是邊緣檢測?
邊緣檢測是一種影像處理技術,用於查詢影像中物件的邊界。它透過檢測亮度的不連續性來工作。邊緣檢測用於影像分割和資料提取,應用領域包括影像處理、計算機視覺和機器視覺。
最常用的邊緣檢測演算法包括:
- Sobel
- Canny
- Prewitt
- Roberts
- 模糊邏輯方法
讓我們考慮以下示例。
import scipy.ndimage as nd import numpy as np im = np.zeros((256, 256)) im[64:-64, 64:-64] = 1 im[90:-90,90:-90] = 2 im = ndimage.gaussian_filter(im, 8) import matplotlib.pyplot as plt plt.imshow(im) plt.show()
上述程式將生成以下輸出。
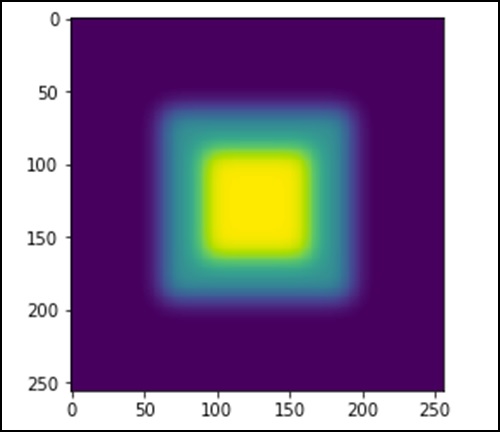
影像看起來像一個彩色的正方形塊。現在,我們將檢測這些彩色塊的邊緣。這裡,ndimage 提供了一個名為Sobel的函式來執行此操作。而 NumPy 提供Hypot函式將兩個結果矩陣組合成一個。
讓我們考慮以下示例。
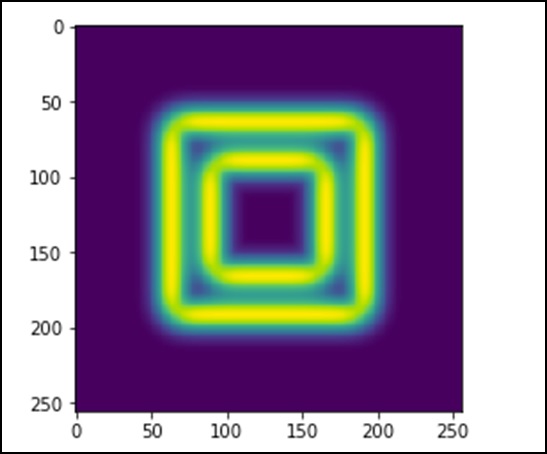
import scipy.ndimage as nd import matplotlib.pyplot as plt im = np.zeros((256, 256)) im[64:-64, 64:-64] = 1 im[90:-90,90:-90] = 2 im = ndimage.gaussian_filter(im, 8) sx = ndimage.sobel(im, axis = 0, mode = 'constant') sy = ndimage.sobel(im, axis = 1, mode = 'constant') sob = np.hypot(sx, sy) plt.imshow(sob) plt.show()
上述程式將生成以下輸出。
SciPy - Optimize (最佳化)
scipy.optimize 包提供了幾個常用的最佳化演算法。該模組包含以下方面:
使用各種演算法(例如 BFGS、Nelder-Mead 單純形、牛頓共軛梯度、COBYLA 或 SLSQP)對多元標量函式進行無約束和約束最小化 (minimize())
全域性(蠻力)最佳化例程(例如,anneal()、basinhopping())
最小二乘法最小化 (leastsq()) 和曲線擬合 (curve_fit()) 演算法
標量單變數函式最小化器 (minimize_scalar()) 和求根器 (newton())
使用各種演算法(例如混合 Powell、Levenberg-Marquardt 或大規模方法,如 Newton-Krylov)的多元方程組求解器 (root())
多元標量函式的無約束和約束最小化
minimize() 函式為scipy.optimize中多元標量函式的無約束和約束最小化演算法提供了一個公共介面。為了演示最小化函式,考慮最小化 NN 變數的 Rosenbrock 函式的問題:
$$f(x) = \sum_{i = 1}^{N-1} \:100(x_i - x_{i-1}^{2})$$
此函式的最小值為 0,當 xi = 1 時達到。
Nelder-Mead 單純形演算法
在以下示例中,minimize() 例程與Nelder-Mead 單純形演算法 (method = 'Nelder-Mead') 一起使用(透過 method 引數選擇)。讓我們考慮以下示例。
import numpy as np from scipy.optimize import minimize def rosen(x): x0 = np.array([1.3, 0.7, 0.8, 1.9, 1.2]) res = minimize(rosen, x0, method='nelder-mead') print(res.x)
上述程式將生成以下輸出。
[7.93700741e+54 -5.41692163e+53 6.28769150e+53 1.38050484e+55 -4.14751333e+54]
單純形演算法可能是最小化相當良好的函式的最簡單方法。它只需要函式評估,並且是簡單最小化問題的不錯選擇。但是,因為它不使用任何梯度評估,所以找到最小值可能需要更長的時間。
另一個只需要函式呼叫就能找到最小值的最佳化演算法是Powell 方法,可以透過在 minimize() 函式中設定 method = 'powell' 來使用。
最小二乘法
求解具有變數邊界的非線性最小二乘問題。給定殘差 f(x)(n 個實變數的 m 維實函式)和損失函式 rho(s)(標量函式),least_squares 找到代價函式 F(x) 的區域性最小值。讓我們考慮以下示例。
在這個例子中,我們找到了沒有自變數邊界的 Rosenbrock 函式的最小值。
#Rosenbrock Function def fun_rosenbrock(x): return np.array([10 * (x[1] - x[0]**2), (1 - x[0])]) from scipy.optimize import least_squares input = np.array([2, 2]) res = least_squares(fun_rosenbrock, input) print res
請注意,我們只提供了殘差向量。該演算法將代價函式構造為殘差平方和,這給出了 Rosenbrock 函式。精確的最小值在 x = [1.0,1.0] 處。
上述程式將生成以下輸出。
active_mask: array([ 0., 0.])
cost: 9.8669242910846867e-30
fun: array([ 4.44089210e-15, 1.11022302e-16])
grad: array([ -8.89288649e-14, 4.44089210e-14])
jac: array([[-20.00000015,10.],[ -1.,0.]])
message: '`gtol` termination condition is satisfied.'
nfev: 3
njev: 3
optimality: 8.8928864934219529e-14
status: 1
success: True
x: array([ 1., 1.])
求根
讓我們瞭解求根如何在 SciPy 中發揮作用。
標量函式
如果只有一個變數方程,則可以嘗試四種不同的求根演算法。這些演算法中的每一個都需要一個區間端點,在這個區間中預期存在根(因為函式符號發生變化)。通常,brentq 是最佳選擇,但在某些情況下或出於學術目的,其他方法可能有用。
不動點求解
與尋找函式的零點密切相關的問題是尋找函式的不動點的問題。函式的不動點是函式求值返回該點的點:g(x) = x。顯然gg的不動點是f(x) = g(x)-x的根。等效地,ff的根是g(x) = f(x)+x的不動點。例程fixed_point提供了一種簡單的迭代方法,使用Aitkens序列加速來估計gg的不動點,如果給定一個起始點。
方程組
可以使用root()函式找到一組非線性方程的根。可以使用多種方法,其中hybr(預設)和 lm 分別使用來自 MINPACK 的Powell 混合方法和Levenberg-Marquardt 方法。
以下示例考慮單變數超越方程。
x2 + 2cos(x) = 0
其根可以如下找到:
import numpy as np from scipy.optimize import root def func(x): return x*2 + 2 * np.cos(x) sol = root(func, 0.3) print sol
上述程式將生成以下輸出。
fjac: array([[-1.]])
fun: array([ 2.22044605e-16])
message: 'The solution converged.'
nfev: 10
qtf: array([ -2.77644574e-12])
r: array([-3.34722409])
status: 1
success: True
x: array([-0.73908513])
SciPy - Stats (統計)
所有統計函式都位於子包scipy.stats中,可以使用info(stats)函式獲得這些函式的相當完整的列表。也可以從 stats 子包的docstring中獲得可用隨機變數的列表。該模組包含大量機率分佈以及不斷增長的統計函式庫。
每個單變數分佈都有自己的子類,如下表所述:
| 序號 | 類和說明 |
|---|---|
| 1 | rv_continuous 一個通用的連續隨機變數類,用於子類化 |
| 2 | rv_discrete 一個通用的離散隨機變數類,用於子類化 |
| 3 | rv_histogram 根據直方圖生成分佈 |
正態連續隨機變數
一個機率分佈,其中隨機變數 X 可以取任何值是連續隨機變數。location (loc) 關鍵字指定均值。scale (scale) 關鍵字指定標準差。
作為rv_continuous類的例項,norm物件繼承了它的通用方法集合,並用特定於此特定分佈的細節來完成它們。
為了計算多個點的 CDF,我們可以傳遞一個列表或一個 NumPy 陣列。讓我們考慮以下示例。
from scipy.stats import norm import numpy as np print norm.cdf(np.array([1,-1., 0, 1, 3, 4, -2, 6]))
上述程式將生成以下輸出。
array([ 0.84134475, 0.15865525, 0.5 , 0.84134475, 0.9986501 , 0.99996833, 0.02275013, 1. ])
為了找到分佈的中位數,我們可以使用百分點函式 (PPF),它是 CDF 的反函式。讓我們透過以下示例來理解。
from scipy.stats import norm print norm.ppf(0.5)
上述程式將生成以下輸出。
0.0
為了生成一系列隨機變數,我們應該使用 size 關鍵字引數,這在以下示例中顯示。
from scipy.stats import norm print norm.rvs(size = 5)
上述程式將生成以下輸出。
array([ 0.20929928, -1.91049255, 0.41264672, -0.7135557 , -0.03833048])
以上輸出不可重現。要生成相同的隨機數,請使用 seed 函式。
均勻分佈
可以使用 uniform 函式生成均勻分佈。讓我們考慮以下示例。
from scipy.stats import uniform print uniform.cdf([0, 1, 2, 3, 4, 5], loc = 1, scale = 4)
上述程式將生成以下輸出。
array([ 0. , 0. , 0.25, 0.5 , 0.75, 1. ])
構建離散分佈
讓我們生成一個隨機樣本,並將觀察到的頻率與機率進行比較。
二項分佈
作為rv_discrete 類的例項,binom 物件繼承了它的通用方法集合,並用特定於此特定分佈的細節來完成它們。讓我們考慮以下示例。
from scipy.stats import uniform print uniform.cdf([0, 1, 2, 3, 4, 5], loc = 1, scale = 4)
上述程式將生成以下輸出。
array([ 0. , 0. , 0.25, 0.5 , 0.75, 1. ])
描述性統計
基本統計資料,例如最小值、最大值、平均值和方差,以NumPy陣列作為輸入並返回相應的結果。scipy.stats包中提供的一些基本統計函式在下面的表格中進行了描述。
| 序號 | 函式及描述 |
|---|---|
| 1 | describe() 計算傳遞陣列的幾個描述性統計量 |
| 2 | gmean() 沿指定的軸計算幾何平均值 |
| 3 | hmean() 沿指定的軸計算調和平均值 |
| 4 | kurtosis() 計算峰度 |
| 5 | mode() 返回眾數值 |
| 6 | skew() 檢驗資料的偏度 |
| 7 | f_oneway() 執行單因素方差分析 (ANOVA) |
| 8 | iqr() 計算資料沿指定軸的四分位間距 |
| 9 | zscore() 計算樣本中每個值的z分數,相對於樣本均值和標準差 |
| 10 | sem() 計算輸入陣列中值的平均值的標準誤差(或測量標準誤差) |
其中許多函式在scipy.stats.mstats中都有類似的版本,這些版本適用於掩碼陣列。讓我們透過下面的示例來了解這一點。
from scipy import stats import numpy as np x = np.array([1,2,3,4,5,6,7,8,9]) print x.max(),x.min(),x.mean(),x.var()
上述程式將生成以下輸出。
(9, 1, 5.0, 6.666666666666667)
T檢驗
讓我們瞭解T檢驗在SciPy中的用途。
ttest_1samp
計算一組分數的均值的T檢驗。這是一個針對零假設的雙尾檢驗,該零假設是獨立觀察樣本‘a’的期望值(均值)等於給定的總體均值popmean。讓我們考慮以下示例。
from scipy import stats rvs = stats.norm.rvs(loc = 5, scale = 10, size = (50,2)) print stats.ttest_1samp(rvs,5.0)
上述程式將生成以下輸出。
Ttest_1sampResult(statistic = array([-1.40184894, 2.70158009]), pvalue = array([ 0.16726344, 0.00945234]))
比較兩個樣本
在以下示例中,有兩個樣本,它們可以來自相同的分佈或不同的分佈,我們想要檢驗這些樣本是否具有相同的統計特性。
ttest_ind - 計算兩個獨立樣本分數均值的T檢驗。這是一個針對零假設的雙尾檢驗,該零假設是兩個獨立樣本具有相同的平均值(期望值)。預設情況下,此檢驗假設總體具有相同的方差。
如果我們觀察到來自相同或不同總體的兩個獨立樣本,我們可以使用此檢驗。讓我們考慮以下示例。
from scipy import stats rvs1 = stats.norm.rvs(loc = 5,scale = 10,size = 500) rvs2 = stats.norm.rvs(loc = 5,scale = 10,size = 500) print stats.ttest_ind(rvs1,rvs2)
上述程式將生成以下輸出。
Ttest_indResult(statistic = -0.67406312233650278, pvalue = 0.50042727502272966)
您可以使用相同長度但均值不同的新陣列來測試相同內容。在loc中使用不同的值並進行相同的測試。
SciPy - CSGraph (壓縮稀疏圖)
CSGraph代表壓縮稀疏圖,它專注於基於稀疏矩陣表示的快速圖演算法。
圖表示
首先,讓我們瞭解什麼是稀疏圖以及它如何幫助圖表示。
什麼是稀疏圖?
圖只是一組節點,它們之間有連結。圖幾乎可以表示任何事物——社交網路連線(每個節點都是一個人,並連線到熟人);影像(每個節點都是一個畫素,並連線到相鄰畫素);高維分佈中的點(每個節點都連線到其最近鄰);以及你能想象到的幾乎任何其他事物。
表示圖資料的一種非常有效的方法是使用稀疏矩陣:我們稱之為G。矩陣G的大小為N x N,G[i, j]給出節點'i'和節點'j'之間連線的值。稀疏圖主要包含零——也就是說,大多數節點只有很少的連線。在大多數感興趣的情況下,此屬性都是正確的。
建立稀疏圖子模組的動機是scikit-learn中使用的幾種演算法,其中包括以下演算法:
Isomap - 一種流形學習演算法,需要在圖中找到最短路徑。
層次聚類 - 基於最小生成樹的聚類演算法。
譜分解 - 基於稀疏圖拉普拉斯運算元的投影演算法。
作為一個具體的例子,假設我們想表示以下無向圖:
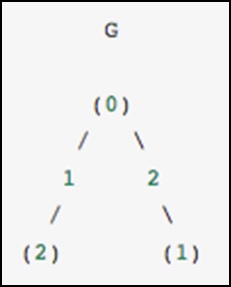
該圖具有三個節點,其中節點0和1由權重為2的邊連線,節點0和2由權重為1的邊連線。我們可以構建密集的、掩碼的和稀疏的表示,如下例所示,記住無向圖由對稱矩陣表示。
G_dense = np.array([ [0, 2, 1],
[2, 0, 0],
[1, 0, 0] ])
G_masked = np.ma.masked_values(G_dense, 0)
from scipy.sparse import csr_matrix
G_sparse = csr_matrix(G_dense)
print G_sparse.data
上述程式將生成以下輸出。
array([2, 1, 2, 1])
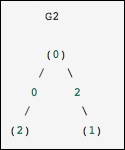
這與之前的圖相同,只是節點0和2由權重為零的邊連線。在這種情況下,上面的密集表示會導致歧義——如果零是一個有意義的值,那麼如何表示非邊?在這種情況下,必須使用掩碼錶示或稀疏表示來消除歧義。
讓我們考慮以下示例。
from scipy.sparse.csgraph import csgraph_from_dense G2_data = np.array ([ [np.inf, 2, 0 ], [2, np.inf, np.inf], [0, np.inf, np.inf] ]) G2_sparse = csgraph_from_dense(G2_data, null_value=np.inf) print G2_sparse.data
上述程式將生成以下輸出。
array([ 2., 0., 2., 0.])
使用稀疏圖的單詞接龍
單詞接龍是由劉易斯·卡羅爾發明的一個遊戲,在這個遊戲中,單詞透過每次更改一個字母來連結。例如:
APE → APT → AIT → BIT → BIG → BAG → MAG → MAN
在這裡,我們用七步從“APE”到“MAN”,每次更改一個字母。問題是——我們能否使用相同的規則找到這兩個單詞之間更短的路徑?這個問題很自然地表達為一個稀疏圖問題。節點將對應於單個單詞,我們將建立連線在最多相差一個字母的單詞對之間的連線。
獲取單詞列表
首先,我們必須獲得有效單詞的列表。我正在執行Mac,Mac在以下程式碼塊中給出的位置有一個詞典。如果您使用的是不同的架構,您可能需要搜尋一下才能找到您的系統詞典。
wordlist = open('/usr/share/dict/words').read().split()
print len(wordlist)
上述程式將生成以下輸出。
235886
現在我們想檢視長度為3的單詞,所以讓我們只選擇那些長度正確的單詞。我們還將消除以大寫字母開頭(專有名詞)或包含非字母數字字元(如撇號和連字元)的單詞。最後,我們將確保所有內容都小寫,以便稍後進行比較。
word_list = [word for word in word_list if len(word) == 3] word_list = [word for word in word_list if word[0].islower()] word_list = [word for word in word_list if word.isalpha()] word_list = map(str.lower, word_list) print len(word_list)
上述程式將生成以下輸出。
1135
現在,我們有1135個有效的三個字母單詞的列表(確切的數字可能會根據使用的特定列表而變化)。這些單詞中的每一個都將成為我們圖中的一個節點,我們將建立連線與僅相差一個字母的單詞對相關的節點的邊。
import numpy as np word_list = np.asarray(word_list) word_list.dtype word_list.sort() word_bytes = np.ndarray((word_list.size, word_list.itemsize), dtype = 'int8', buffer = word_list.data) print word_bytes.shape
上述程式將生成以下輸出。
(1135, 3)
我們將使用每個點之間的漢明距離來確定哪些單詞對是連線的。漢明距離衡量兩個向量之間不同條目的分數:任何兩個漢明距離等於1/N的單詞,其中N是單詞中字母的數量,在單詞接龍中是連線的。
from scipy.spatial.distance import pdist, squareform from scipy.sparse import csr_matrix hamming_dist = pdist(word_bytes, metric = 'hamming') graph = csr_matrix(squareform(hamming_dist < 1.5 / word_list.itemsize))
在比較距離時,我們不使用等式,因為這對於浮點值來說可能不穩定。只要單詞列表中沒有兩個條目相同,不等式就會產生所需的結果。現在,我們的圖已經設定好了,我們將使用最短路徑搜尋來查詢圖中任意兩個單詞之間的路徑。
i1 = word_list.searchsorted('ape')
i2 = word_list.searchsorted('man')
print word_list[i1],word_list[i2]
上述程式將生成以下輸出。
ape, man
我們需要檢查這些是否匹配,因為如果這些單詞不在列表中,輸出將出現錯誤。現在,我們只需要找到圖中這兩個索引之間的最短路徑。我們將使用迪傑斯特拉演算法,因為它允許我們僅查詢一個節點的路徑。
from scipy.sparse.csgraph import dijkstra distances, predecessors = dijkstra(graph, indices = i1, return_predecessors = True) print distances[i2]
上述程式將生成以下輸出。
5.0
因此,我們看到“ape”和“man”之間的最短路徑僅包含五個步驟。我們可以使用演算法返回的前驅來重建此路徑。
path = [] i = i2 while i != i1: path.append(word_list[i]) i = predecessors[i] path.append(word_list[i1]) print path[::-1]i2]
上述程式將生成以下輸出。
['ape', 'ope', 'opt', 'oat', 'mat', 'man']
SciPy - Spatial (空間資料)
scipy.spatial包可以透過利用Qhull庫來計算一組點的三角剖分、沃羅諾伊圖和凸包。此外,它還包含用於最近鄰點查詢的KDTree實現以及用於各種度量中距離計算的實用程式。
德勞內三角剖分
讓我們瞭解什麼是德勞內三角剖分以及它們如何在SciPy中使用。
什麼是德勞內三角剖分?
在數學和計算幾何中,給定平面中離散點集P的德勞內三角剖分是三角剖分DT(P),這樣P中沒有點位於DT(P)中任何三角形的圓周內。
我們可以透過SciPy計算相同的內容。讓我們考慮以下示例。
from scipy.spatial import Delaunay points = np.array([[0, 4], [2, 1.1], [1, 3], [1, 2]]) tri = Delaunay(points) import matplotlib.pyplot as plt plt.triplot(points[:,0], points[:,1], tri.simplices.copy()) plt.plot(points[:,0], points[:,1], 'o') plt.show()
上述程式將生成以下輸出。

共麵點
讓我們瞭解什麼是共麵點以及它們如何在SciPy中使用。
什麼是共麵點?
共麵點是位於同一平面上的三個或更多個點。回想一下,平面是一個平面,它向各個方向無限延伸。它通常在數學教科書中顯示為一個四面體。
讓我們看看如何使用SciPy找到它。讓我們考慮以下示例。
from scipy.spatial import Delaunay points = np.array([[0, 0], [0, 1], [1, 0], [1, 1], [1, 1]]) tri = Delaunay(points) print tri.coplanar
上述程式將生成以下輸出。
array([[4, 0, 3]], dtype = int32)
這意味著點4位於三角形0和頂點3附近,但不包含在三角剖分中。
凸包
讓我們瞭解什麼是凸包以及它們如何在SciPy中使用。
什麼是凸包?
在數學中,歐幾里得平面或歐幾里得空間(或更一般地,實數上的仿射空間)中的一組點X的凸包或凸包絡是最小的凸集,它包含X。
讓我們考慮以下示例以詳細瞭解它。
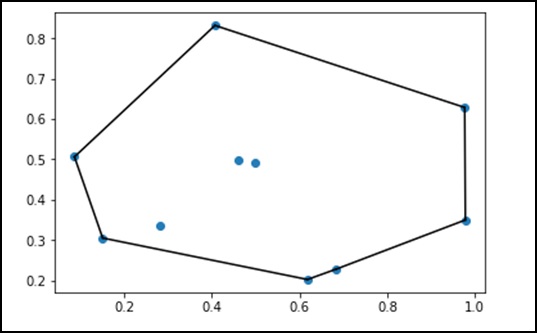
from scipy.spatial import ConvexHull points = np.random.rand(10, 2) # 30 random points in 2-D hull = ConvexHull(points) import matplotlib.pyplot as plt plt.plot(points[:,0], points[:,1], 'o') for simplex in hull.simplices: plt.plot(points[simplex,0], points[simplex,1], 'k-') plt.show()
上述程式將生成以下輸出。
SciPy - ODR (正交距離迴歸)
ODR代表正交距離迴歸,用於迴歸研究。基本線性迴歸通常用於透過在圖上繪製最佳擬合線來估計兩個變數y和x之間的關係。
為此使用的一種數學方法稱為最小二乘法,其目的是最小化每個點的平方誤差之和。這裡關鍵的問題是如何計算每個點的誤差(也稱為殘差)?
在標準線性迴歸中,目標是根據X值預測Y值——因此,明智的做法是計算Y值的誤差(如下圖中的灰色線所示)。但是,有時更明智的做法是同時考慮X和Y的誤差(如下圖中的紅色虛線所示)。
例如:當您知道您的X測量值不確定時,或者當您不想關注一個變數的誤差超過另一個變數時。
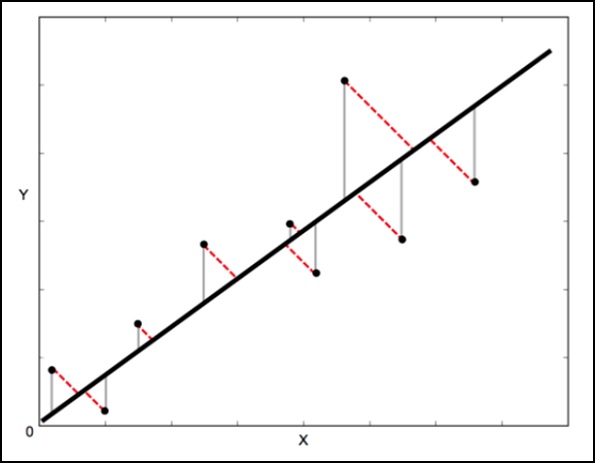
正交距離迴歸(ODR)是一種可以做到這一點的方法(在這種情況下,正交意味著垂直——因此它計算垂直於線的誤差,而不僅僅是“垂直”)。
scipy.odr對單變量回歸的實現
以下示例演示了scipy.odr對單變量回歸的實現。
import numpy as np import matplotlib.pyplot as plt from scipy.odr import * import random # Initiate some data, giving some randomness using random.random(). x = np.array([0, 1, 2, 3, 4, 5]) y = np.array([i**2 + random.random() for i in x]) # Define a function (quadratic in our case) to fit the data with. def linear_func(p, x): m, c = p return m*x + c # Create a model for fitting. linear_model = Model(linear_func) # Create a RealData object using our initiated data from above. data = RealData(x, y) # Set up ODR with the model and data. odr = ODR(data, linear_model, beta0=[0., 1.]) # Run the regression. out = odr.run() # Use the in-built pprint method to give us results. out.pprint()
上述程式將生成以下輸出。
Beta: [ 5.51846098 -4.25744878] Beta Std Error: [ 0.7786442 2.33126407] Beta Covariance: [ [ 1.93150969 -4.82877433] [ -4.82877433 17.31417201 ]] Residual Variance: 0.313892697582 Inverse Condition #: 0.146618499389 Reason(s) for Halting: Sum of squares convergence
SciPy - Special Package (特殊函式包)
special包中提供的函式是通用函式,它們遵循廣播和自動陣列迴圈。
讓我們看看一些最常用的特殊函式:
- 三次根函式
- 指數函式
- 相對誤差指數函式
- 對數和指數函式
- 朗伯函式
- 排列和組合函式
- 伽馬函式
現在讓我們簡要了解一下這些函式。
三次根函式
此三次方根函式的語法為 – scipy.special.cbrt(x)。這將獲取x 的逐元素立方根。
讓我們考慮以下示例。
from scipy.special import cbrt res = cbrt([10, 9, 0.1254, 234]) print res
上述程式將生成以下輸出。
[ 2.15443469 2.08008382 0.50053277 6.16224015]
指數函式
指數函式的語法為 – scipy.special.exp10(x)。這將計算 10**x 的逐元素值。
讓我們考慮以下示例。
from scipy.special import exp10 res = exp10([2, 9]) print res
上述程式將生成以下輸出。
[1.00000000e+02 1.00000000e+09]
相對誤差指數函式
此函式的語法為 – scipy.special.exprel(x)。它生成相對誤差指數 (exp(x) - 1)/x。
當x 接近零時,exp(x) 接近 1,因此 exp(x) - 1 的數值計算可能會遭受災難性的精度損失。然後實現 exprel(x) 來避免當x 接近零時發生的精度損失。
讓我們考慮以下示例。
from scipy.special import exprel res = exprel([-0.25, -0.1, 0, 0.1, 0.25]) print res
上述程式將生成以下輸出。
[0.88479687 0.95162582 1. 1.05170918 1.13610167]
對數和指數函式
此函式的語法為 – scipy.special.logsumexp(x)。它有助於計算輸入元素指數和的對數。
讓我們考慮以下示例。
from scipy.special import logsumexp import numpy as np a = np.arange(10) res = logsumexp(a) print res
上述程式將生成以下輸出。
9.45862974443
朗伯函式
此函式的語法為 – scipy.special.lambertw(x)。它也稱為蘭伯特 W 函式。蘭伯特 W 函式 W(z) 定義為 w * exp(w) 的反函式。換句話說,W(z) 的值使得對於任何複數 z,z = W(z) * exp(W(z))。
蘭伯特 W 函式是一個多值函式,具有無限多個分支。每個分支給出了方程 z = w exp(w) 的一個單獨解。這裡,分支由整數 k 索引。
讓我們考慮以下示例。這裡,蘭伯特 W 函式是 w exp(w) 的反函式。
from scipy.special import lambertw w = lambertw(1) print w print w * np.exp(w)
上述程式將生成以下輸出。
(0.56714329041+0j) (1+0j)
排列與組合
讓我們分別討論排列和組合以便更清晰地理解它們。
組合 − 組合函式的語法為 – scipy.special.comb(N,k)。讓我們考慮以下示例 −
from scipy.special import comb res = comb(10, 3, exact = False,repetition=True) print res
上述程式將生成以下輸出。
220.0
注意 − 僅當 exact = False 時才接受陣列引數。如果 k > N,N < 0 或 k < 0,則返回 0。
排列 − 組合函式的語法為 – scipy.special.perm(N,k)。從 N 個事物中取 k 個事物的排列,即 N 的 k 排列。這也稱為“部分排列”。
讓我們考慮以下示例。
from scipy.special import perm res = perm(10, 3, exact = True) print res
上述程式將生成以下輸出。
720
伽馬函式
伽馬函式通常被稱為廣義階乘,因為 z*gamma(z) = gamma(z+1),對於自然數 'n',gamma(n+1) = n!。
組合函式的語法為 – scipy.special.gamma(x)。從 N 個事物中取 k 個事物的排列,即 N 的 k 排列。這也稱為“部分排列”。
組合函式的語法為 – scipy.special.gamma(x)。從 N 個事物中取 k 個事物的排列,即 N 的 k 排列。這也稱為“部分排列”。
from scipy.special import gamma res = gamma([0, 0.5, 1, 5]) print res
上述程式將生成以下輸出。
[inf 1.77245385 1. 24.]