
- SciPy 教程
- SciPy - 主頁
- SciPy - 簡介
- SciPy - 環境設定
- SciPy - 基本功能
- SciPy - 叢集
- SciPy - 常量
- SciPy - FFTpack
- SciPy - 整合
- SciPy - 插值
- SciPy - 輸入和輸出
- SciPy - 線性代數
- SciPy - Ndimage
- SciPy - 最佳化
- SciPy - 統計
- SciPy - CSGraph
- SciPy - 空間
- SciPy - ODR
- SciPy - 特殊包
- SciPy 有用資源
- SciPy - 參考
- SciPy - 快速指南
- SciPy - 有用資源
- SciPy - 討論
SciPy - ODR
ODR 表示正交距離迴歸,應用於迴歸研究。基本線性迴歸通常用於估計變數y和x之間的關係,方法是在圖表上繪製最佳擬合線。
為此使用的數學方法稱為最小二乘法,目的是最小化每個點的平方誤差之和。這裡的主要問題是,你如何計算每個點的誤差(也稱為殘差)?
在標準線性迴歸中,目的是根據 X 值預測 Y 值,因此明智的做法是計算 Y 值中的誤差(如下圖中以灰色線顯示)。然而,有時更加明智的做法是考慮 X 和 Y 的誤差(如下圖標註的紅點所示)。
例如,當你瞭解 X 的測量值不確定時,或者不想關注變數相對於其他變數的誤差時。
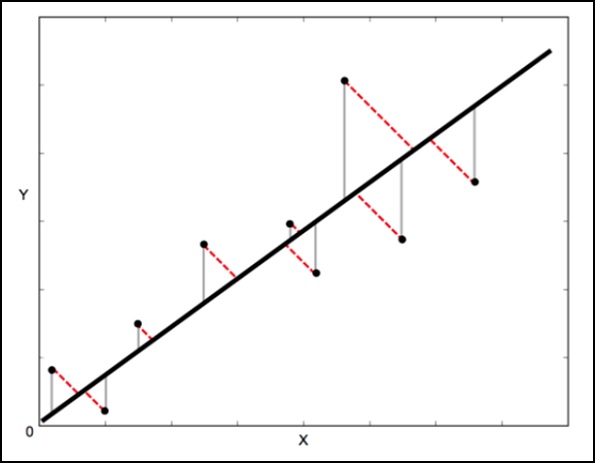
正交距離迴歸 (ODR) 是一種能夠做到這一點的方法(此上下文中的正交表示垂直,因此它計算與線相垂直的誤差,而不僅僅是“垂直”的誤差)。
scipy.odr 在一元迴歸方面的實現
以下示例說明了一元迴歸中的 scipy.odr 的實現。
import numpy as np import matplotlib.pyplot as plt from scipy.odr import * import random # Initiate some data, giving some randomness using random.random(). x = np.array([0, 1, 2, 3, 4, 5]) y = np.array([i**2 + random.random() for i in x]) # Define a function (quadratic in our case) to fit the data with. def linear_func(p, x): m, c = p return m*x + c # Create a model for fitting. linear_model = Model(linear_func) # Create a RealData object using our initiated data from above. data = RealData(x, y) # Set up ODR with the model and data. odr = ODR(data, linear_model, beta0=[0., 1.]) # Run the regression. out = odr.run() # Use the in-built pprint method to give us results. out.pprint()
以上程式將生成以下輸出。
Beta: [ 5.51846098 -4.25744878] Beta Std Error: [ 0.7786442 2.33126407] Beta Covariance: [ [ 1.93150969 -4.82877433] [ -4.82877433 17.31417201 ]] Residual Variance: 0.313892697582 Inverse Condition #: 0.146618499389 Reason(s) for Halting: Sum of squares convergence
廣告