電力電子 - 效能引數

---

---

確定不同變流器的效能引數非常重要，這些變流器的拓撲結構可以是單相或多相。

假設

• 所用器件為理想器件，即不考慮任何損耗
• 器件具有電阻負載

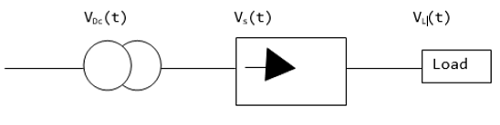
負載上的直流電壓

$$V_{DC}=\frac{1}{T} \int_{0}^{T}V_{L}\left ( t \right )dt$$

負載上的有效電壓

$$V_{L}=\sqrt{\frac{1}{T}}\int_{0}^{T}V_{L}^{2}\left ( t \right )dt$$

波形因子

$$FF=\frac{V_{L}}{V_{DC}}$$

紋波係數

$$RF=\frac{\sqrt{V_{L}^{2}-V_{DC}^{2}}}{V_{DC}}=\sqrt{FF^{2}-1}$$

效率（整流因子）

$$\eta =\frac{P_{DC}}{P_{L}+P_{D}}$$

其中以上定義為 -

$P_{DC}=V_{DC}\times I_{DC}$

$P_{L}=V_{L}\times I_{L}$

$P_{D}=R_{D}\times I_{L}^{2}$（$P_{D}$ 為整流器損耗，$R_{D}$ 為電阻）

$$\eta =\frac{V_{DC}I_{DC}}{\left ( V_{L}I_{L} \right )+\left ( R_{D}I_{L}^{2} \right )}=\frac{V_{DC}^{2}}{V_{L}^{2}}\times \frac{1}{1+\frac{R_{D}}{R_{L}}}$$

但 $R_{D}=0$

因此，

$$\eta =\left ( \frac{V_{DC}}{V_{L}} \right )^{2}=\left ( \frac{1}{FF}\right )^{2}$$

變壓器利用率

$$TUF=\frac{P_{DC}}{VA \:額定值 \:of \:the \:Transformer }=\frac{P_{DC}}{\frac{VA_{p}+VA_{s}}{2}}$$

VA_p 和 VA_s 是變壓器的一次側和二次側功率額定值。