電力電子 - 斬波器

---

---

斬波器使用高速連線和斷開電源負載。透過連續觸發功率開關的通/斷，間歇地將固定直流電壓施加到電源負載。功率開關保持通或斷的時間段分別稱為斬波器的通態時間和斷態時間。

斬波器主要應用於電動汽車、風能和太陽能轉換以及直流電機調速器。

斬波器的符號

斬波器的分類

根據輸出電壓，斬波器可分為：

• 升壓斬波器（升壓轉換器）
• 降壓斬波器（降壓轉換器）
• 升/降壓斬波器（降壓-升壓轉換器）

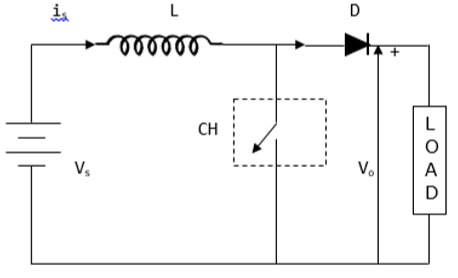
升壓斬波器

升壓斬波器的平均輸出電壓 (V_o) 大於輸入電壓 (V_s)。下圖顯示了升壓斬波器的配置。

電流和電壓波形

當斬波器接通時，V₀（平均輸出電壓）為正，當斬波器斷開時為負，如下面的波形所示。

其中

T_ON – 斬波器接通的時間間隔

T_OFF – 斬波器斷開的時間間隔

V_L – 負載電壓

V_s – 源電壓

T – 斬波週期 = T_ON + T_OFF

V_o 由下式給出：

$$V_{0}=\frac{1}{T}\int_{0}^{T_{ON}}V_{S}dt$$

當斬波器 (CH) 接通時，負載短路，因此，T_ON期間的輸出電壓為零。此外，在此期間電感充電。這使得 V_S = V_L

$L\frac{di}{dt}=V_{S},$ $\frac{\Delta i}{T_{ON}}=\frac{V_{S}}{L}$

因此，$\Delta i=\frac{V_{S}}{L}T_{ON}$

Δi = 電感峰峰值電流。當斬波器 (CH) 斷開時，電感 L 發生放電。因此，V_s 和 V_L 的總和如下：

$V_{0}=V_{S}+V_{L},\quad V_{L}=V_{0}-V_{S}$

但是 $L\frac{di}{dt}=V_{0}-V_{S}$

因此，$L\frac{\Delta i}{T_{OFF}}=V_{0}-V_{S}$

這給出，$\Delta i=\frac{V_{0}-V_{S}}{L}T_{OFF}$

將通態的 Δi 與斷態的 Δi 相等得到：

$\frac{V_{S}}{L}T_{ON}=\frac{V_{0}-V_{S}}{L}T_{OFF}$, $V_{S}\left ( T_{ON}+T_{OFF} \right )=V_{0}T_{OFF}$

$V_{0}=\frac{TV_{S}}{T_{OFF}}=\frac{V_{S}}{\frac{\left ( T+T_{ON} \right )}{T}}$

這給出平均輸出電壓為：

$$V_{0}=\frac{V_{S}}{1-D}$$

上述方程表明 V_o 可以從 V_S 變化到無窮大。它證明輸出電壓將始終大於輸入電壓，因此，它會提升或增加電壓水平。

降壓斬波器

這也被稱為降壓轉換器。在這種斬波器中，平均輸出電壓 V_O 小於輸入電壓 V_S。當斬波器接通時，V_O = V_S，當斬波器斷開時，V_O = 0

當斬波器接通時：

$V_{S}=\left ( V_{L}+V_{0} \right ),\quad V_{L}=V_{S}-V_{0},\quad L\frac{di}{dt}=V_{S}-V_{0},\quad L\frac{\Delta i}{T_{ON}}=V_{s}+V_{0}$

因此，峰峰值負載電流由下式給出：

$\Delta i=\frac{V_{s}-V_{0}}{L}T_{ON}$

電路圖

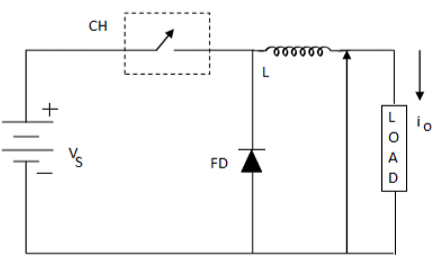
其中 FD 是續流二極體。

當斬波器斷開時，電感發生極性反轉和放電。電流透過續流二極體和電感流向負載。這給出：

$$L\frac{di}{dt}=V_{0}........................................\left ( i \right )$$

改寫為：$\quad L\frac{\Delta i}{T_{OFF}}=V_{0}$

$$\Delta i=V_{0}\frac{T_{OFF}}{L}...................................\left ( ii \right )$$

聯立方程 (i) 和 (ii) 得到：

$\frac{V_{S}-V_{0}}{L}T_{ON}=\frac{V_{0}}{L}T_{OFF}$

$\frac{V_{S}-V_{0}}{V_{0}}=\frac{T_{OFF}}{T_{ON}}$

$\frac{V_{S}}{V_{0}}=\frac{T_{ON}-T_{OFF}}{T_{ON}}$

上述方程給出：

$$V_{0}=\frac{T_{ON}}{T}V_{S}=DV_{S}$$

方程 (i) 給出：

$\Delta i=\frac{V_{S}-DV_{S}}{L}DT$, 由 $D=\frac{T_{ON}}{T}$

$=\frac{V_{S}-\left ( 1-D \right )D}{Lf}$

$f=\frac{1}{T}=$斬波頻率

電流和電壓波形

電流和電壓波形如下：

對於降壓斬波器，輸出電壓始終小於輸入電壓。這由下面的波形所示。

升/降壓斬波器

這也被稱為降壓-升壓轉換器。它可以提高或降低輸入電壓水平。下圖顯示了一個降壓-升壓斬波器。

當斬波器接通時，電感 L 由源電壓 V_s 充電。因此，V_s = V_L。

$$L\frac{di}{dt}=V_{S}$$ $$\Delta i=\frac{V_{S}}{L}T_{ON}=\frac{V_{S}}{L}T\frac{T_{ON}}{T}=\frac{DV_{S}}{Lf}$$

因為：

$D=\frac{T_{ON}}{T}$ 且 $f=\frac{1}{T} .............................................. \left ( iii \right )$

當斬波器斷開時，電感的極性反轉，這導致它透過二極體和負載放電。

因此，

$$V_{0}=-V_{L}$$ $$L\frac{di}{dt}=-V_{0}$$

$L\frac{\Delta i}{T_{OFF}}=-V_{0}$, 因此 $\Delta i=-\frac{V_{0}}{L}T_{OFF}................................\left ( iv \right )$

評估方程 (iii) 和 (iv) 得到：

$\frac{DV_{S}}{Lf}=-\frac{V_{0}}{L}T_{OFF}$, $DV_{S}=-DV_{S}=-V_{0}T_{OFF}f$

$DV_{S}=-V_{0}\frac{T-T_{ON}}{T}=-V_{0}\left ( 1-\frac{T_{ON}}{T} \right )$, $V_{0}=-\frac{DV_{S}}{1-D}$

因為 $D=\frac{T_{ON}}{T}=\frac{T-T_{OFF}}{1-D}$

這給出：

$V_{0}=\frac{DV_{S}}{1-D}$

D 可以從 0 變化到 1。當 D = 0 時；V_O = 0

當 D = 0.5 時，V_O = V_S

當 D = 1 時，V_O = ∞。

因此，在 0 ≤ D ≤ 0.5 的區間內，輸出電壓在 0 ≤ V_O < V_S 的範圍內變化，我們得到降壓或降壓操作。而在 0.5 ≤ D ≤ 1 的區間內，輸出電壓在 V_S ≤ V_O ≤ ∞ 的範圍內變化，我們得到升壓或升壓操作。