資料結構
網路
關係型資料庫管理系統
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 語言程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理
化學
生物
數學
英語
經濟學
心理學
社會學
服裝設計
法律研究火車 A 的行駛路徑由方程 $3x\ +\ 4y\ -\ 12\ =\ 0$ 給出，另一輛火車 B 的行駛路徑由方程 $6x\ +\ 8y\ -\ 48\ =\ 0$ 給出。請用圖形表示這種情況。
已知
火車 A 的行駛路徑由方程 $3x\ +\ 4y\ -\ 12\ =\ 0$ 給出，另一輛火車 B 的行駛路徑由方程 $6x\ +\ 8y\ -\ 48\ =\ 0$ 給出。
要求
我們需要用圖形表示上述情況。
解答
給定的方程組為
$3x\ +\ 4y\ -\ 12\ =\ 0$....(i)
$4y=12-3x$
$y=\frac{12-3x}{4}$
$6x\ +\ 8y\ -\ 48\ =\ 0$....(ii)
$8y=48-6x$
$y=\frac{48-6x}{8}$
為了用圖形表示上述方程，我們需要每個方程至少兩個解。
對於方程 (i)，
如果 $x=0$，則 $y=\frac{12-3(0)}{4}=\frac{12}{4}=3$
如果 $y=0$，則 $0=\frac{12-3x}{4}$
$12=3x$
$x=\frac{12}{3}=4$
| $x$ | $0$ | $4$ |
$y=\frac{12-3x}{4}$ | $3$ | $0$ |
對於方程 (ii)，
如果 $x=0$，則 $y=\frac{48-6(0)}{8}=\frac{48}{8}=6$
如果 $y=0$，則 $0=\frac{48-6x}{8}$
$\Rightarrow 6x=48$
$\Rightarrow x=\frac{48}{6}=8$
| $x$ | $0$ | $8$ |
| $y=\frac{48-6x}{8}$ | $6$ | $0$ |
上述情況可以用圖形表示如下
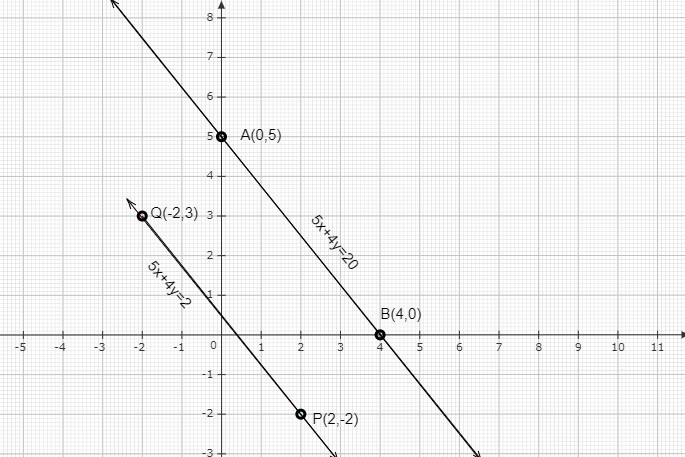
直線 AB 表示方程 $6x+8y-48=0$，直線 PQ 表示方程 $3x+4y-12=0$。
更新於: 2022-10-10
34 次檢視
廣告