一座塔頂的仰角觀察為\( 60^{\circ} . \) 在第一個觀察點垂直向上 \( 30 \mathrm{m} \) 的位置，仰角被發現為 \( 45^{\circ} . \) 求

(i) 塔的高度，

(ii) 它到觀察點的水平距離。

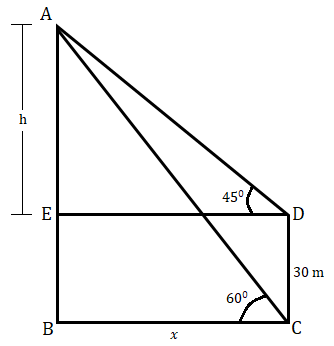
在上圖中，AB 表示塔。點 C 是第一個觀察點，從該點的仰角為 60^o。點 D 比點 C 高 30 米，從該點的仰角為 45^o。ED 平行於 BC。 

現在，

設 BC = x 米，AE = h 米。

現在，

在 ∆ABC 中

$ \begin{array}{l}
tan\ 60\ =\ \frac{h\ +\ 30}{x}\\
\\
\\
\sqrt{3} \ =\ \frac{h\ +\ 30}{x}\\
\\
\\
x\sqrt{3} \ =\ h\ +\ 30\ \ \ \ \ \ ...( i)
\end{array}$

在 ∆ADE 中

$ \begin{array}{l}
tan\ 45\ =\ \frac{h}{x}\\
\\
\\
1\ =\ \frac{h}{x}\\
\\
\\
x\ =\ h\ \ \ \ \ \ \ \ ...( ii)
\end{array}$

將 x 的值代入方程 (i)

$ \begin{array}{l}
h\ =\ \frac{30}{\sqrt{3} \ -\ 1}\\
\\
\\
h\ =\ \frac{30}{1.732\ -\ 1}\\
\\
\\
h\ =\ \frac{30}{0.732}\\
\\
\\
h\ =\ 40.98\ m\\
\\
\\
h\ =\ 41\ m
\end{array}$

所以，根據方程 (ii)

x = 41 m

現在，

i)  塔的高度 = h + 30 = 41 + 30 = 71 m

ii)  到觀察點的水平距離 = x = 41 m

教程點

更新於： 2022 年 10 月 10 日

72 次檢視

開啟你的 職業生涯

完成課程獲得認證

開始學習