證明等邊三角形的三個角都為60°。

待辦事項

我們必須證明等邊三角形的三個角都為60°。

解答

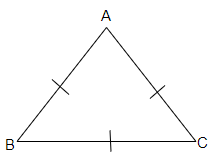
讓我們考慮一個等邊三角形ABC

我們有：

AB=BC=AC (根據圖示)

我們知道：

等角對等邊。

因此：

∠A=∠B=∠C

我們也知道：

三角形的內角和始終等於180°

這意味著

在△ABC中：

∠A+∠B+∠C = 180°

因此：

3∠A=180° (因為∠A=∠B=∠C)

∠A=180°/3

∠A= 60°

因此：

∠A=∠B=∠C=60°

因此，等邊三角形的三個角都為60°。

教程點

更新於：2022年10月10日

60次瀏覽

開啟你的職業生涯

完成課程獲得認證

開始學習