在下圖中，ABCD是一個邊長為2a的正方形。求該正方形內切圓和外接圓面積之比。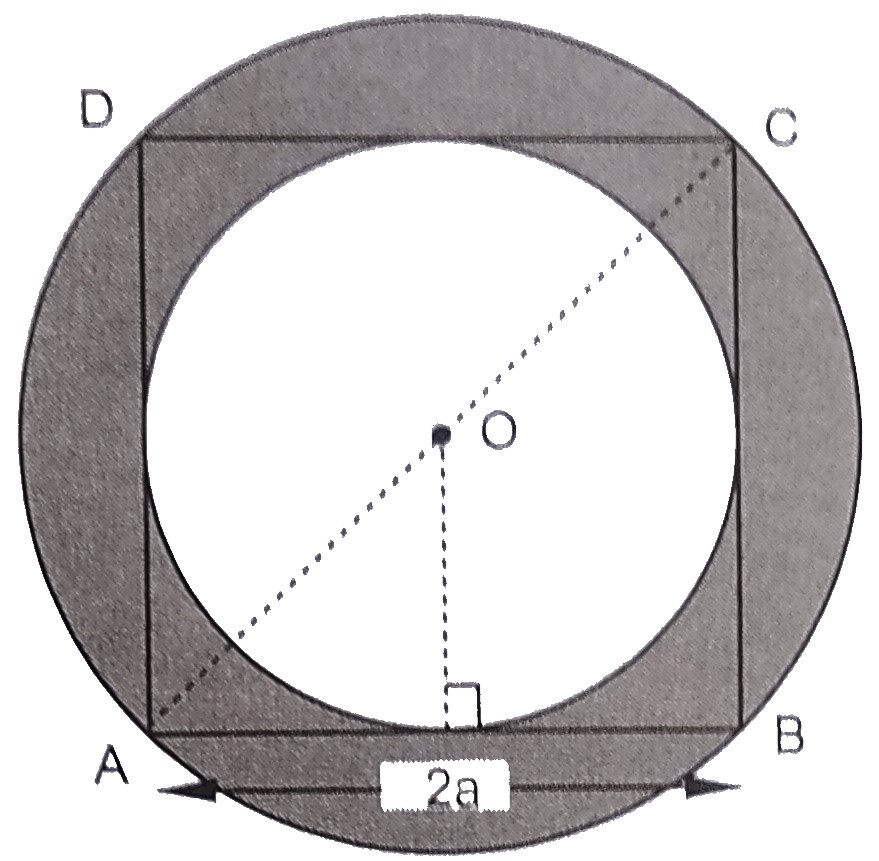

已知

ABCD是一個邊長為2a的正方形。

要求：

我們要求出該正方形內切圓和外接圓面積之比。

解答

正方形ABCD內接於一個圓。
正方形邊長 = 2a

由圖可知：

外接圓直徑AC = 正方形對角線

= √2 × 2a

= 2√2 a

這意味著：

外接圓半徑R = AC/2

= (2√2 a) / 2

= √2 a

內切圓直徑 = 2a

內切圓半徑r = 2a/2 = a

因此：

正方形內切圓和外接圓面積之比 = 內切圓面積 / 外接圓面積

= πr² / πR²

= π(√2 a)² / π(a)²

= 2πa² / πa²

= 2/1

正方形內切圓和外接圓面積之比為2:1。

Tutorialspoint

更新於：2022年10月10日

瀏覽量：111

開啟你的職業生涯

完成課程獲得認證

開始學習