如果一個正方形內接於一個圓，求圓和正方形面積的比值。

已知

一個正方形內接於一個圓。

要求

我們必須找到圓和正方形面積的比值。

解答

設 $r$ 為圓的半徑，$s$ 為正方形的邊長。

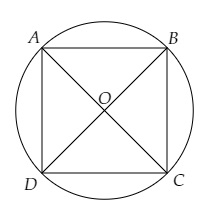
這意味著，

$AB = BC = CD = DA = s$

$AC$ 和 $BD$ 是正方形的對角線。

正方形的對角線 $AC$ = 圓的直徑

$\Rightarrow \sqrt{2} s=2 r$

$\Rightarrow s=\frac{2 r}{\sqrt{2}}$

圓的面積 $=\pi r^{2}$

正方形的面積 $=s^{2}$

圓和正方形面積的比值 $=\frac{\pi r^{2}}{s^{2}}$

$=\frac{22 r^{2}}{7 \times(\frac{2 r}{\sqrt{2}})^{2}}$

$=\frac{22 r^{2}}{7 \times \frac{4 r^{2}}{2}}$

$=\frac{22 r^{2} \times 2}{7 \times 4 r^{2}}$

$=\frac{11}{7}$

圓和正方形面積的比值為 $11:7$。

教程點

更新於: 2022年10月10日

88 次瀏覽

開啟你的 職業生涯

透過完成課程獲得認證

開始學習