Swift程式：計算內接於正方形的圓的面積

---

本教程將討論如何編寫Swift程式來計算內接於正方形的圓的面積。

我們有一個圖形，其中一個圓內接於一個正方形。這意味著圓心和正方形中心相同，圓的直徑等於正方形的邊長。如果我們至少有一個正方形或圓的測量值，那麼我們可以很容易地計算出正方形的面積和周長，或圓的面積和周長。

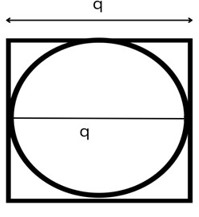
在這裡，我們使用以下公式找到內接於正方形的圓的面積：

(丌/4)*q*q

這裡，q是圓的半徑和正方形的邊長。

上述公式的推導

假設q是正方形的邊長

圓的面積是πr²。

我們知道邊長和圓的直徑相等。所以，半徑是：

r = q/2

因此，內接於正方形的圓的面積是：

A = 丌(q/2)2 = (丌/4)q2

下面是相同的演示：

輸入

假設我們的給定輸入是：

side = 15

輸出

期望輸出為：

Area of the circle inscribed in square = 176.71458676442586

演算法

以下是演算法：

步驟1 - 建立一個具有返回值的函式。

步驟2 - 使用以下公式找到內接於正方形的圓的面積

return (Double.pi/4) * q * q

步驟3 - 呼叫函式並將圓的邊長作為引數傳遞。

步驟4 - 列印輸出。

示例

以下程式演示瞭如何計算內接於正方形的圓的面積。

import Foundation
import Glibc

// Creating a function to find the area of

// circle inscribed in square
func inscribedCircleArea(q:Double) -> Double{
   return (Double.pi/4) * q * q
}
var num = 10.0
print("Side of the square is", num)
print("Area of the circle inscribe in square:", inscribedCircleArea(q:num))

輸出

Side of the square is 10
Area of the circle inscribe in square: 78.53981633974483

在上面的程式中，我們建立了一個函式，它使用以下公式返回內接於正方形的圓的面積：

return (Double.pi/4) * q * q

這裡，`Double.pi`用於訪問預定義的π值。