資料結構
網路
關係資料庫管理系統
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 語言程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理學
化學
生物學
數學
英語
經濟學
心理學
社會學
服裝設計
法律研究求一個內接於半徑為 8 釐米的圓的正方形的面積。
已知：一個內接於半徑為 8 釐米的圓的正方形。
要求：求正方形的面積。
解答
設正方形為 ABCD，內接於圓中。
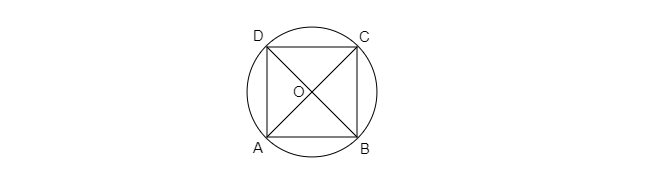
因此，半徑 r=OA=OB=OC=OD=8 釐米
△ABC 是直角三角形，因為 OA=8，OC=8
AC=8+8=16
根據勾股定理，
斜邊的平方 = 其他兩邊的平方和。
⇒ AC²=AB²+BC²
因為 ABCD 是正方形，所以所有邊都相等，AB=BC
⇒ AC²=2AB²
⇒ 16²=2AB²
∴ AB=8√2
因此，正方形的邊長 = 8√2
正方形的面積 = (8√2)²=128 平方釐米
更新於： 2022 年 10 月 10 日
254 次瀏覽
廣告