在下圖中，\( ABCD \) 是邊長為 \( 2a \) 的正方形。求兩個圓周長的比例。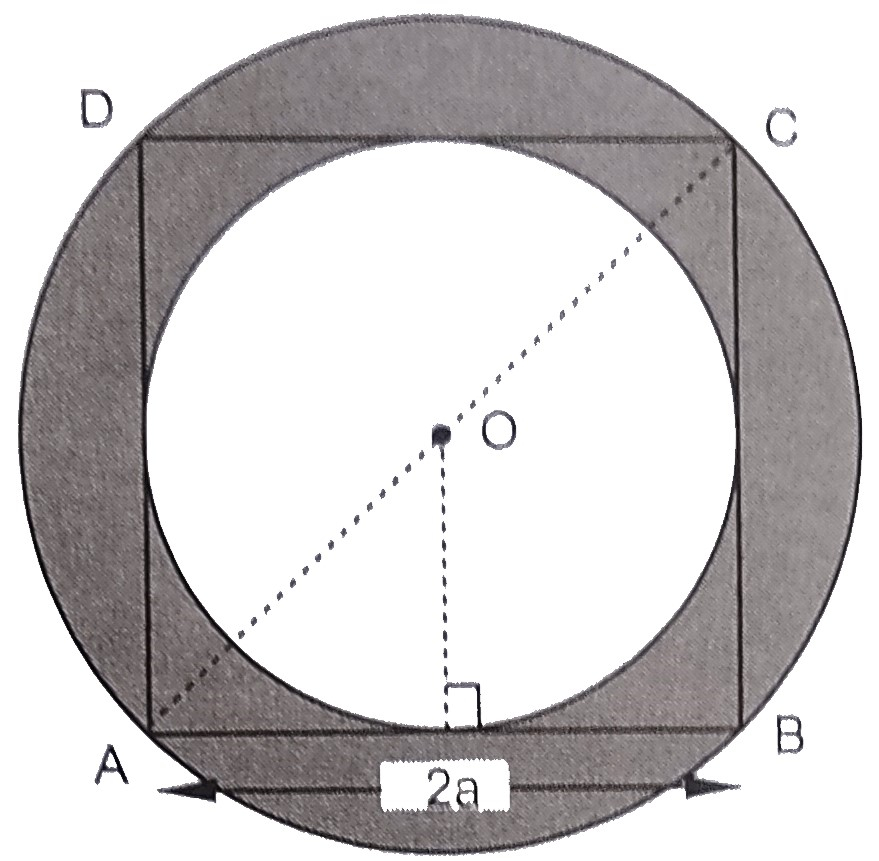

已知

\( ABCD \) 是邊長為 \( 2a \) 的正方形。

要求：

我們要求出兩個圓周長的比例。

解答

正方形 ABCD 內接於一個圓。
正方形邊長 = 2a

從圖中，

外圓直徑 AC = 正方形對角線

$= \sqrt{2} \times 2a$

$= 2\sqrt{2}a$

這意味著，

外圓半徑 R = AC/2

$= \frac{2\sqrt{2}a}{2}$

$= \sqrt{2}a$

內圓直徑 = 2a

內圓半徑 r = 2a/2 = a

因此，

兩個圓周長的比例 = 外圓周長 / 內圓周長

$= \frac{2\pi R}{2\pi r}$

$= \frac{R}{r}$

$= \frac{\sqrt{2}a}{a}$

$= \frac{\sqrt{2}}{1}$

兩個圓周長的比例是 √2:1。

Tutorialspoint

更新於：2022年10月10日

瀏覽量：132

開啟你的職業生涯

完成課程獲得認證

開始學習