在下圖中，AB + BC + CD + DA
答案。

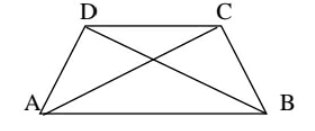
解答

設對角線AC和BD相交於點O。

由於三角形中任意兩邊之和大於第三邊。因此，

在△AOB中，AB < OA + OB ……….(i)

在△BOC中，BC < OB + OC ……….(ii)

在△COD中，CD < OC + OD ……….(iii)

在△AOD中，DA < OD + OA ……….(iv)

⇒ AB + BC + CD + DA < 2OA + 2OB + 2OC +

2OD ⇒ AB + BC + CD + DA < 2[(AO + OC) + (DO

+ OB)] ⇒ AB + BC + CD + DA < 2(AC + BD)

因此，得證。

Tutorialspoint

更新於：2022年10月10日

69 次瀏覽

開啟您的職業生涯

完成課程獲得認證

開始學習