資料結構
網路
關係型資料庫管理系統
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理
化學
生物
數學
英語
經濟學
心理學
社會學
時尚研究
法律研究如果 $P$ 是平行四邊形 $ABCD$ 內部任意一點，則證明三角形 $APB$ 的面積小於平行四邊形面積的一半。
已知
$P$ 是平行四邊形 $ABCD$ 內部任意一點。
要求
我們需要證明三角形 $APB$ 的面積小於平行四邊形面積的一半。
解答
連線 $AP$ 和 $BP$。
作 $DN \perp AB$ 和 $PM \perp AM$。
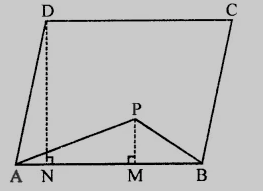
平行四邊形 $\mathrm{ABCD}$ 的面積 = $\mathrm{AB} \times \mathrm{DN}$..........(i)
三角形 $\mathrm{APB}$ 的面積 = $\frac{1}{2} \mathrm{AB} \times \mathrm{PM}$...............(ii)
由 (i) 和 (ii) 可得，
$\mathrm{DN}>\mathrm{PM}$ 或 $\mathrm{PM}
$\mathrm{AB} \times \mathrm{PM}
$\frac{1}{2} \mathrm{AB} \times \mathrm{PM}
$\operatorname{ar}(\Delta \mathrm{PAB})
證畢。
更新時間: 2022年10月10日
50 次瀏覽
廣告