如圖所示，求與三角形$\vartriangle AOB$三個頂點等距的點的座標。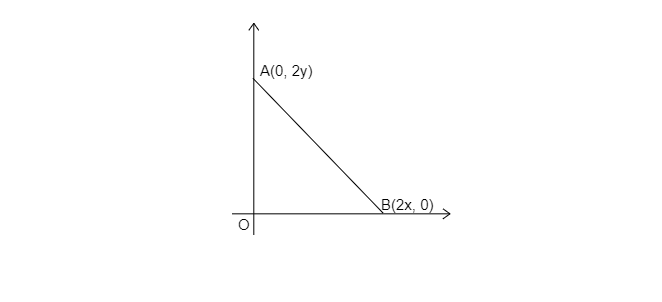"\n

已知：一點與$\vartriangle AOB$的頂點等距。

求解：求該點的座標。

解答

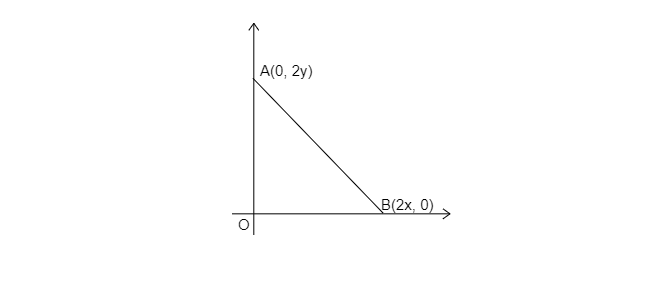
在圖中，三角形的頂點為：

$A( 0,\ 2y),\ B( 2x,\ 0)$ 和 $O( 0,\ 0)$。

這是一個直角三角形。

與三角形頂點等距的點稱為該三角形的外心。

對於直角三角形，外心是斜邊的中點。

因此，這裡外心的座標必須是$AB$的中點$=( \frac{x_1+x_2}{2},\ \frac{y_1+y_2}{2})$

$=( \frac{0+2x}{2},\ \frac{2y+0}{2})$

$=( \frac{2x}{2},\ \frac{2y}{2})$

$=( x,\ y)$

因此，$( x,\ y)$與$\vartriangle AOB$的頂點等距。

教程點

更新於: 2022年10月10日

65 次瀏覽

開啟你的職業生涯

透過完成課程獲得認證

開始學習