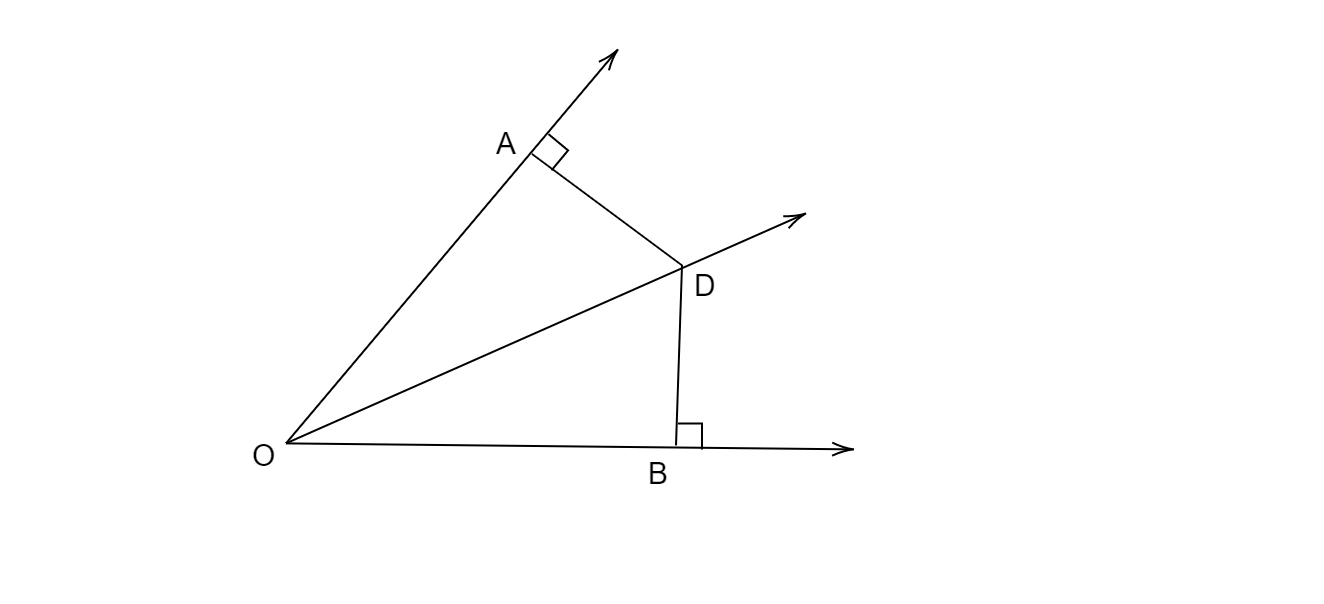
$CD$ 平分 $\angle AOB$，$DA$ 和 $DB$ 分別是從點 $D$ 向射線 $OA$ 和 $OB$ 作的垂線。證明 $DA=DB$。
"\n

已知：$OD$ 平分 $\angle AOB$，且 $DA$ 和 $DB$ 分別是從點 $D$ 向射線 $OA$ 和 $OB$ 作的垂線。

求證：$DA=DB$。

我們有

$\angle AOD = \angle BOD$ …… $( i)$ ….. 因為 OD 平分 $\angle AOB$ (已知)

$\angle OAD = \angle OBD = 90^{o}$ …… (ii) ……. [DA 和 DB 分別是從點 D 向射線 OA 和 OB 作的垂線 (已知)]

現在，考慮 $\vartriangle ADO$ 和 $\vartriangle BDO$，我們有

$\angle AOD = \angle BOD$ …… 由 $( i)$

$OD = OD$ …… [兩個三角形的公共邊]

$\angle OAD = \angle OBD$ …… 由 $( ii)$

$\therefore$ 根據 ASA 全等，$\vartriangle ADO \cong \vartriangle BDO$

我們知道，如果兩個或多個三角形彼此全等，那麼它們的所有對應角和對應邊也全等。這個性質被稱為全等三角形的對應邊相等，簡稱“C.P.C.T”。

$\therefore DA = DB$