資料結構
網路
關係資料庫管理系統 (RDBMS)
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C語言程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理學
化學
生物學
數學
英語
經濟學
心理學
社會學
服裝設計
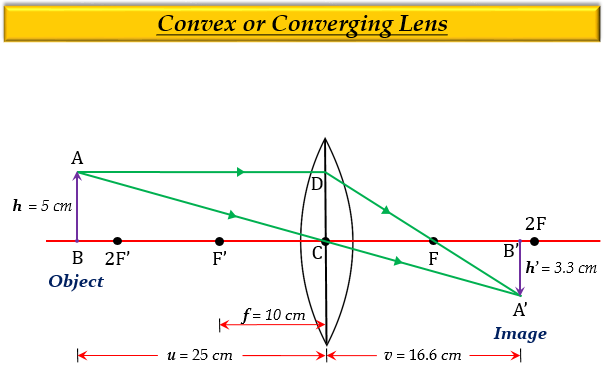
法學一個高5釐米的物體放在距離焦距為10釐米的會聚透鏡25釐米處。求所成像的位置、大小和性質。並畫出光路圖。
已知
物距，$u$ = $-$25 cm (因為物體總是放置在透鏡左側，所以取負值)
焦距，$f$ = 10 cm
物體高度 $h$ = $+$5 cm
求解：像的位置、性質、$v$ 和像的大小 $h'$。
解答
根據透鏡公式，我們知道
$\frac {1}{v}-\frac {1}{u}=\frac {1}{f}$
將已知值代入公式，我們得到：
$\frac {1}{v}-\frac {1}{(-25)}=\frac {1}{10}$
$\frac {1}{v}+\frac {1}{25}=\frac {1}{10}$
$\frac {1}{v}=\frac {1}{10}-\frac {1}{25}$
$\frac {1}{v}=\frac {5-2}{50}$
$\frac {1}{v}=\frac {3}{50}$
$v=\frac {50}{3}$
$v=+16.6\ cm$
因此，像距 $v$ 為 16.6 cm，像距的正號 $(+)$ 表示像形成在 透鏡右側（透鏡後）。我們知道，在透鏡右側形成 實像。
現在，
根據放大率公式，我們知道
$m=\frac {v}{u}=\frac {h'}{h}$
將已知值代入公式，我們得到：
$\frac {\frac {50}{3}}{-25}=\frac {h'}{5}$
$\frac {50}{-25\times {3}}=\frac {h'}{5}$
$-\frac {2}{3}=\frac {h'}{5}$
$h'=-\frac {10}{3}$ [交叉相乘]
$h'=-3.3cm$
因此，像的大小 $h'$ 為 3.3 cm，負號 $(-)$ 表示像是 倒立的（在主軸下方）。
因此，像的 位置在 透鏡後（右側），像的 性質是 實像且倒立，像的 大小比物體 小（3.3 cm）。
瀏覽量：387
