資料結構
網路
關係資料庫管理系統 (RDBMS)
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 語言程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理
化學
生物
數學
英語
經濟學
心理學
社會研究
服裝研究
法律研究一個風箏由一個對角線為 32 釐米的正方形和一個底邊為 8 釐米、兩腰各為 6 釐米的等腰三角形組成，如圖 12.17 所示，並使用三種不同的顏色。每種顏色的紙張用量是多少？圖 (12.16)
已知：一個風箏由一個對角線為 32 釐米的正方形和一個底邊為 8 釐米、兩腰各為 6 釐米的等腰三角形組成，如圖所示。
求解：每種顏色的紙張用量是多少？
解答
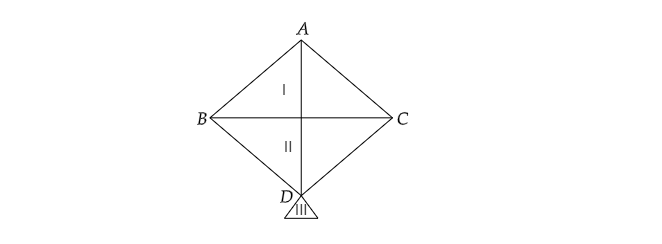
設風箏由正方形 ABCD 和等腰三角形 DEF 組成。
已知，三角形 DEF 的邊長 DE=DF=6 釐米，EF=8 釐米，正方形 ABCD 的對角線為 32 釐米。
我們知道：
正方形的對角線互相垂直平分。
OA=OB=OC=OD=32/2=16 釐米
AO 垂直於 BC，DO 垂直於 BC。
區域 I 的面積 = 三角形 ABC 的面積 = 直角三角形的面積 = 1/2 × 底 × 高 = 1/2 × BC × OA
區域 I 的面積 = 1/2 × 32 × 16 = 256 平方釐米
同樣，區域 II 的面積 = 256 平方釐米
對於區域 III：
在三角形 DEF 中
設邊 a=6 釐米，b=6 釐米，c=8 釐米
三角形的半周長，s=(a+b+c)/2=(6+6+8)/2 釐米=10 釐米
使用海倫公式：
區域 III（三角形）的面積 = √[s(s-a)(s-b)(s-c)]
= √[10(10-6)(10-6)(10-8)]
= √(10×4×4×2)
= √(2×5×4×4×2)
= √(2×2×4×4×5)
= 2×4√5
= 8×2.24=17.92 平方釐米
因此，製作風箏時使用的 I 顏色紙張面積 = 256 平方釐米
製作風箏時使用的 II 顏色紙張面積 = 256 平方釐米
製作風箏時使用的 III 顏色紙張面積 = 17.92 平方釐米
更新於：2022 年 10 月 10 日
30 次瀏覽
廣告