Python 中的 Regula Falsi 方法建模

---

在本教程中，我將向您展示如何藉助 Regula Falsi 方法（也稱為“假位置法”）找到方程的根。讓我們考慮下圖所示。

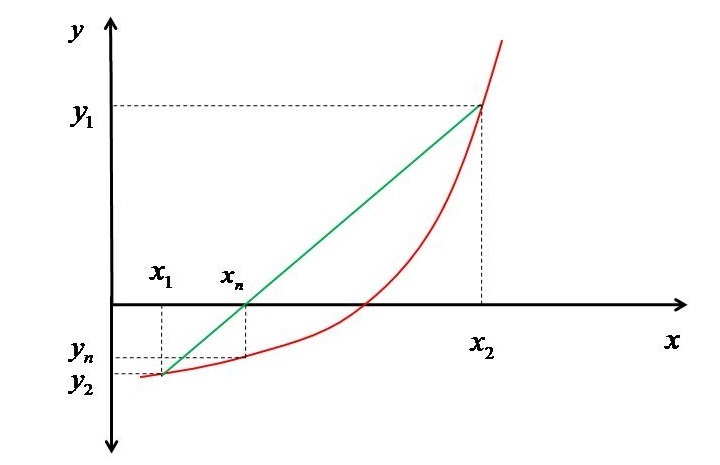
首先，我們搜尋了兩個 𝑥 值 $\mathrm{x_{1}}$ 和 $\mathrm{x_{2}}$，在這些值處函式的值 ($\mathrm{y_{1}} $和 $\mathrm{y_{2}}$) 不同，這意味著這些點應該使得這兩個值的乘積為負（即，它們應該位於 X 軸的兩側）。由於這些不是精確點，即根存在的點，因此它們被視為假點，因此稱為 Regula Falsi 方法。現在，這些點將由一條線連線，該線將在 $\mathrm{x_{n}}$ 點與 x 軸相交。現在，對應於此將計算 $y_{n}$。

如果 $\mathrm{y_{1}}$ 和 $\mathrm{y_{n}}$ 的乘積小於 0，則表示 $\mathrm{x_{1}}$ 和 $\mathrm{x_{n}}$ 位於根的兩側。然後，$\mathrm{x_{2}}$ 將被 $\mathrm{x_{n}}$ 替換，$\mathrm{y_{2}}$ 將被 $\mathrm{y_{1}}$ 替換。否則，它將表明 $\mathrm{x_{1}}$ 和 $\mathrm{x_{𝑛}}$ 位於同一側，然後 $\mathrm{x_{1}}$ 將被 $\mathrm{x_{n}}$ 替換，$\mathrm{y_{1}}$ 將被 $\mathrm{y_{n}}$ 替換。此後，將重複相同的過程，直到 $y_{n}$ 的絕對值小於某個收斂準則（這裡我們將其設定為 0.00001，但您可以根據所需的精度自由選擇）。

現在問題是如何計算新的位置 $\mathrm{x_{n}}$。新的位置可以透過經過 ($x_{1},y_{1}$) 和 ($x_{2},y_{2}$) 的直線方程得到，如下所示 -

$$\mathrm{y-y_{1}=\tfrac{\left \{ y_{2}-y_{1} \right \}}{\left \{ x_{2}-x_{1} \right \}}(x-x_{1})}$$

但在 $\mathrm{x_{n}}$ 處，𝑦 截距為零，則上述方程變為

$$\mathrm{0-y_{1}=\tfrac{\left \{ y_{2}-y_{1} \right \}}{\left \{ x_{2}-x_{1} \right \}}(x_{n}-x_{1})}$$

$$\mathrm{0-\tfrac{\left \{ x_{2}-x_{1} \right \}}{\left \{ y_{2}-y_{1} \right \}}y_{_{1}}=(x_{n}-x_{1})}$$

$$\mathrm{x_{1}-\tfrac{\left \{ x_{2}-x_{1} \right \}}{\left \{ y_{2}-y_{1} \right \}}y_{_{1}}=x_{n}}$$

最終，用於計算新 𝑥 值 ($x_{n}$) 的方程變為 -

$$\mathrm{x_{n}=x_{1}-\tfrac{\left \{ x_{2}-x_{1} \right \}}{\left \{ y_{2}-y_{1} \right \}}y_{_{1}}}$$

Python 中 Regula Falsi 方法的實現

我們試圖使用 Regula Falsi 方法找到其根的函式是 $\mathrm{𝑥^{3}}$−9𝑥−5=0。初始區間選擇為 (−3,−1)。

匯入用於陣列使用和資料繪圖的模組 -

from pylab import *

定義要計算其根的多項式的函式 -

f=lambda x: x**3-9*x-5

此步驟雖然不是嚴格必要的，但它將有助於視覺化 Regula Falsi 過程的工作原理。這段程式碼將有助於繪製函式 -

# Creating array of x
x=linspace(-4,4,50)

# Drawing function
figure(1,dpi=200)
plot(x,f(x))
ylim(-19,10)
plot([-4,4],[0,0],'k--')

選擇您期望根存在的初始區間。我所取的值是上面提到的多項式。

# Selecting false positions x1 and x2
x1=-3
x2=-1

# Evaluating corresponding y1 and y2
y1=f(x1)
y2=f(x2)

檢查初始猜測區間 ($\mathrm{𝑥_{1},𝑥_{2}}$) 是否正確，即 $\mathrm{𝑦_{1}x𝑦_{2}}$>0。

如果不是，則使用適當的訊息退出迴圈。否則，進入 while 迴圈。在 while 迴圈內，首先根據公式 1 計算 $\mathrm{𝑥_{𝑛}}$ 並找到 $\mathrm{𝑦_{ℎ}}$。

如果 $\mathrm{𝑦_{1}}$ 的絕對值本身很小，則使用最終答案 $\mathrm{𝑥_{1}}$ 中斷 while 迴圈。否則，檢查 $\mathrm{y_{1}\:X\:y_{n}s0}$ 是否為真，如果是，則設定 $\mathrm{x_{2}=x_{n}}$ 和 $\mathrm{𝑦_{2}=𝑦_{𝑛}}$。否則，設定 $\mathrm{𝑥_{1}=𝑥_{𝑛}}$ 和 $\mathrm{𝑦_{1}=𝑦_{𝑛}}$。

# Initial check
if y1*y2>0:
   print("on the same side of x axis, Correct the Range")
   exit
else:
   # Plotting line joining (x1,y1) and (x2,y2)
   plot([x1,x2],[y1,y2])
   
   # Iteration counter
   count=1
   
   # Iterations
   while True:
      xn=x1-y1*(x2-x1)/(y2-y1)
      plot([xn],[0],'o',label=f'{xn}')
      yn=f(xn)
      if abs(y1)<1.E-5:
         print("Root= ",x1)
         break
      elif y1*yn<0:
         x2=xn
         y2=yn
         plot([x1,x2],[y1,y2])
      else:
         x1=xn
         y1=yn
         plot([x1,x2],[y1,y2])
         
      # printing few xn in legend
      if count<6:
         legend()
         
      # Increasing iteration counter
      count +=1
   show()

程式的 輸出 將是 -

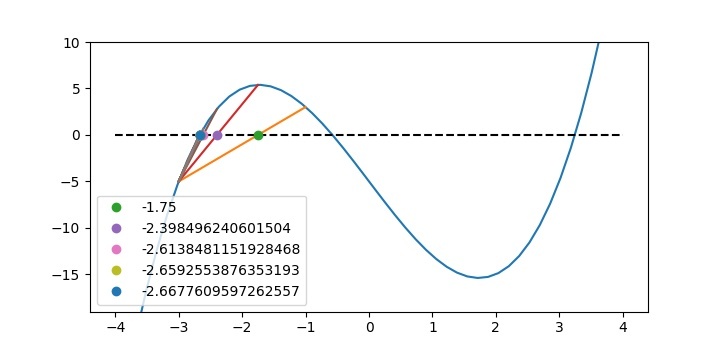
Root= -2.669663840642225

函式圖本身顯示了對根的收斂，如下所示。

完整的 Python 程式碼

最終編譯後的程式碼如下 -

# Importing modules for plotting and Array
from pylab import *

# Defining function using Lambda
f = lambda x: x ** 3 - 9 * x - 5

# Creating array of x using linspace
x = linspace(-4, 4, 50)

# Drawing function for better understanding of convergence
figure(1, figsize=(7.20,3.50))
plot(x, f(x))
ylim(-19, 10)
plot([-4, 4], [0, 0], 'k--')

# Selecting false position interval x1 and x2
x1 = -3
x2 = -1

# Evaluating the values at x1 and x2 viz. y1 and y2
y1 = f(x1)
y2 = f(x2)

# Initial check for gussed interval
if y1 * y2 > 0:
   print("on the same side of x axis, Correct the Range")
   exit
else:
   # Plotting line joining (x1,y1) and (x2,y2)
   plot([x1, x2], [y1, y2])

   # Iteration counter
   count = 1

   # Iterations
   while True:
      xn = x1 - y1 * (x2 - x1) / (y2 - y1)
      plot([xn], [0], 'o', label=f'{xn}')
      yn = f(xn)
      if abs(y1) < 1.E-5:
         print("Root= ", x1)
         break
      elif y1 * yn < 0:
         x2 = xn
         y2 = yn
         plot([x1, x2], [y1, y2])
      else:
         x1 = xn
         y1 = yn
         plot([x1, x2], [y1, y2])

      # printing few xn
      if count < 6:
         legend()
      # Incrementing counter
      count += 1
   show()

對於其他根，我們必須採用其他初始集合的 $\mathrm{x_{1}}$ 和 $\mathrm{x_{2}}$。您可以練習 (-1, 1) 和 (2, 4)。

結論

在本教程中，您學習瞭如何在 Python 中建模 Regula Falsi 方法。您還了解了初始猜測區間的選擇有多麼重要。