資料結構
網路
關係資料庫管理系統(RDBMS)
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C語言程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理學
化學
生物學
數學
英語
經濟學
心理學
社會學
服裝學
法學Python中的卡諾迴圈建模
卡諾迴圈是最基本的燃氣動力迴圈。它是任何發動機迴圈的基準。每個發動機迴圈效率都以卡諾迴圈作為檢驗標準。如果發明者開發了一個新的發動機迴圈，則必須針對基準（即卡諾迴圈）進行驗證。
所有熱力學迴圈都具有卡諾迴圈所確定的上限。它包含兩個可逆絕熱過程和兩個等溫過程，總共四個過程。等溫過程涉及熱量的新增和排放，而可逆絕熱過程涉及功的相互作用。下圖顯示了卡諾迴圈的示意圖。
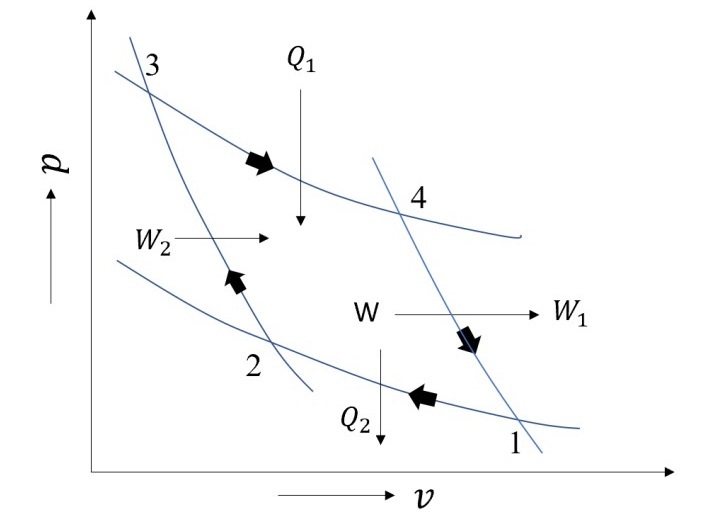
熱量排放和新增在步驟1-2和3-4中等溫進行。而過程4-1和2-3是可逆絕熱過程，分別透過功從迴圈中輸入和輸出。
在對迴圈進行建模時，需要考慮最大壓力（$\mathrm{p_{max}}$）、最小壓力（$\mathrm{p_{min}}$）、最大體積（$\mathrm{V_{max}}$）、壓縮比（𝑟）和絕熱指數（𝛾）等輸入變數。下面解釋了幾個過程的熱力學計算。
過程 1-2：（等溫過程）
過程 1-2 是一個等溫過程。這裡，
$$\mathrm{p_{1}\:=\:p_{min}}$$
$$\mathrm{v_{1}\:=\:v_{max}}$$
使用壓縮比 (r)，可以根據點 1 處的體積評估點 2 處的第一個體積，如下所示：
$$\mathrm{v_{2}\:=\:\frac{v_{1}}{r}}$$
然後計算步驟 1-2 期間的等溫常數，如下所示：
$$\mathrm{c_{1}\:=\:p_{1}\:\times\:v_{1}}$$
一旦知道 $\mathrm{c_{1}}$，就可以評估沿線 1-2 的壓力變化，如下所示：
$$\mathrm{p\:=\:\frac{c_{1}}{v}}$$
過程 2-3（可逆絕熱過程）
過程 2-3 是一個可逆絕熱過程。這裡，
$$\mathrm{p_{3}\:=\:p_{max}}$$
設 $\mathrm{c_{2}}$ 為絕熱線的常數。由於絕熱線和等溫線在點 2 相交，因此可以計算 $\mathrm{c_{2}}$ 為
$$\mathrm{p_{2}\:=\:\frac{c_{2}}{v_{2}^{\gamma}}\:=\:\frac{c_{1}}{v_{2}}}$$
$$\mathrm{c_{2}\:=\:c_{1}\:\times\:v_{2}^{\gamma\:-\:1}}$$
由於 $\mathrm{c_{2}}$ 也滿足點 3，因此可以計算點 3 處的體積，如下所示：
$$\mathrm{v_{3}\:=\:\left ( \frac{c_{2}}{p_{3}} \right )^{\frac{1}{\gamma }}}$$
可以評估沿 2-3 的壓力變化，如下所示：
$$\mathrm{p\:=\:\frac{c_{2}}{v^{\gamma}}}$$
過程 3-4（等溫過程）
設線 3-4 的常數為 $\mathrm{c_{3}}$。由於 $\mathrm{p_{3}}$ 和 $\mathrm{v_{3}}$ 都已知，並且點 3 也穿過它們，因此沿等溫線的常數計算如下：
$$\mathrm{c_{3}\:=\:p_{3}\:\times\:v_{3}}$$
此外，為了評估沿 3-4 的壓力波動，需要知道沿 4-1 的常數。假設它是 $\mathrm{c_{4}}$，並且由於 $\mathrm{c_{4}}$ 也滿足點 1，因此評估如下：
$$\mathrm{c_{4}\:=\:p_{1}\:\times\:v_{1}^{\gamma}}$$
因此，可以評估 $\mathrm{v_{4}}$ 為：
$$\mathrm{v_{4}\:=\:\left ( \frac{c_{4}}{c_{3}} \right )^{\frac{1}{\gamma\:-\:1 }}}$$
因此，可以評估沿 3-4 的壓力變化為：
$$\mathrm{p\:=\:\frac{c_{3}}{v}}$$
過程 4-1（可逆絕熱）
已知 $\mathrm{c_{4}}$ 和 1 和 4 處的體積，可以計算沿 4-1 的壓力變化，如下所示：
$$\mathrm{p\:=\:\frac{c_{4}}{v^{\gamma}}}$$
用於模擬卡諾迴圈的 Python 程式碼
用於模擬卡諾迴圈的 Python 函式如下所示：
from pylab import * from pandas import * # Carnot Cycle def carnot(p_min,p_max,v_max,r,gma): font = {'family':'Times New Roman', 'size':16} figure(figsize=(7.50,5.50)) rc('font', **font) '''This function prints the carnot cycle The arguments are as follows: p_min: minimum pressure p_max: Maximum pressure v_max: Maximum volume r: compression ratio gma: Adiabatic exponent The order of arguments is: p_min,p_max,v_max,r,gma''' p1=p_min v1=v_max v2=v1/r c1=p1*v1 # Process 1-2 v=linspace(v2,v1,100) p=c1/v plot(v,p/1000,'r-',linewidth=3) p2=c1/v2 # Process 2-3 p3=p_max c2=c1*v2**(gma-1.) v3=(c2/p3)**(1/gma) v=linspace(v3,v2,100) p=c2/v**gma plot(v,p/1000,'b',linewidth=3) # Process 3-4 c3=p3*v3 c4=p1*v1**gma v4=(c4/c3)**(1/(gma-1.)) v=linspace(v3,v4,100) p=c3/v plot(v,p/1000,'g',linewidth=3) p4=c3/v4 # Process 4-1 v=linspace(v4,v1,100) p=c4/v**gma plot(v,p/1000,'c',linewidth=3) title('Carnot Cycle',size='large',color='k') xlabel('Volume ($m^3$)') ylabel('Pressure (kPa)') grid(linestyle='--', color='k') axis([0.,v_max+0.01,1*10**5/10**3,21*10**5/10**3]) text(v1,p1/1000,'1') text(v2,p2/1000-200,'2') text(v3+0.01,p3/1000-20,'3') text(v4,p4/1000,'4') data={ 'p':[p1,p2,p3,p4], 'v':[v1,v2,v3,v4], 'c':[c1,c2,c3,c4], 'State': [1,2,3,4] } df=DataFrame(data) savefig('Carnot_final.jpg') return df.set_index('State') carnot(2*10**5,20*10**5,0.5,5,1.4) show()
對於 $\mathrm{p_{min}\:=\:2\:\times\:10^{5}\:Pa}$，$\mathrm{p_{max}\:=\:20\:\times\:10^{5}\:Pa}$，$\mathrm{v_{max}\:=\:0.5\:m^{3}}$，$\mathrm{r\:=\:5}$ 和 $\mathrm{\gamma\:=\:1.4}$，獲得的結果如下圖所示：
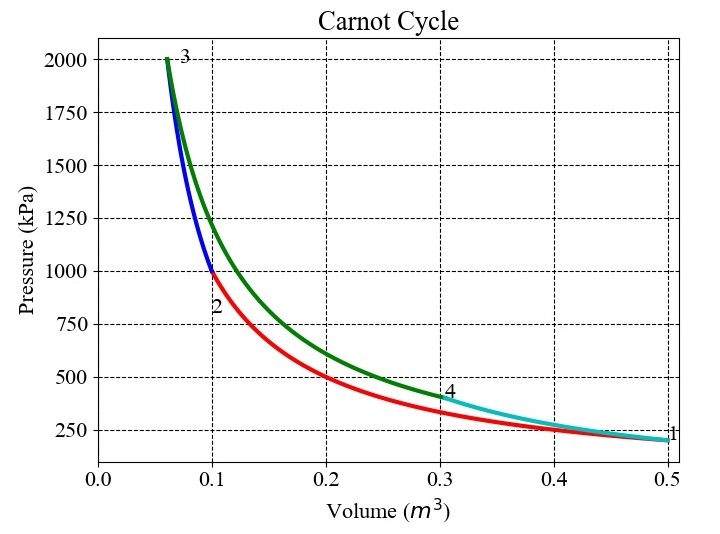
不同狀態點的壓力、體積值如下所示：
狀態 |
p |
v |
|---|---|---|
1 |
200000.0 |
0.500000 |
2 |
1000000.0 |
0.100000 |
3 |
2000000.0 |
0.060951 |
4 |
400000.0 |
0.304753 |
結論
在本教程中，已經介紹了模擬卡諾迴圈的方法。已經介紹了一個 Python 函式，並進行了一個測試用例來演示函式的使用。該函式能夠根據輸入資料繪製迴圈。
948 次瀏覽
