資料結構
網路
關係資料庫管理系統 (RDBMS)
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C語言程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理學
化學
生物學
數學
英語
經濟學
心理學
社會研究
服裝研究
法律研究Python中的高斯-塞德爾方法建模
高斯-塞德爾方法是一種迭代方法，用於求解任何線性方程組。雖然該方法與雅可比方法非常相似，但在高斯-塞德爾方法中，在一個迭代中獲得的未知數(x)的值在同一個迭代中使用，而在雅可比方法中，它們在下一個迭代級別使用。在同一步驟中更新x可以加快收斂速度。
線性方程組可以寫成：
$$\mathrm{a_{1,1}x_{1} \: + \: a_{1,2}x_{2} \: + \: \dotso \: + \: a_{1,n}x_{n} \: = \: b_{1}}$$
$$\mathrm{a_{2,1}x_{1} \: + \: a_{2,2}x_{2} \: + \: \dotso \: + \: a_{2,n}x_{n} \: = \: b_{2}}$$
$$\mathrm{\vdots}$$
$$\mathrm{a_{n,1}x_{1} \: + \: a_{n,2}x_{2} \: + \: \dotso \: + \: a_{n,n}x_{n} \: = \: b_{n}}$$
因此，一般情況下，高斯-塞德爾方法可以寫成：
$$\mathrm{x_{i_{new}} \: = \: − \frac{1}{a_{i,i}}(\sum_{j=1,j \neq i}^n a_{i,j}x_{j_{new}} \: − \: b_{i})}$$
其中，$\mathrm{x_{j_{new}}}$ 是在同一迭代迴圈中剛剛求解的方程中獲得的x的新值。
高斯-塞德爾演算法可以總結如下：
從對未知數 (x) 的一些初始猜測陣列開始。
透過將x的猜測值代入如下所示的方程重新排列形式來計算新的x：
$$\mathrm{x_{i_{new}} \: = \: − \frac{1}{a_{i,i}}(\sum_{j=1,j \neq i}^n a_{i,j}x_{j_{new}} \: − \: b_{i})}$$
現在$\mathrm{i_{new}}$ 將是當前迭代中獲得的新的x值。
下一步是評估新值和猜測值之間的誤差，即$\mathrm{\lvert x_{new} \: − \: x_{guess} \rvert}$。如果誤差大於某個收斂標準（我們將其設為$\mathrm{10^{−5}}$），則將新值賦給舊猜測值，即$\mathrm{x_{guess} \: = \: x_{new}}$，然後開始下一次迭代。
否則，$\mathrm{x_{new}}$ 是最終答案。
重要的是要記住，方程的對角佔優性（通常稱為斯卡伯勒準則）適用於高斯-塞德爾方法。如果滿足以下條件，則保證高斯-塞德爾方法的收斂性：
$$\mathrm{\frac{\sum_{i\neq j \lvert a_{i,j} \rvert}}{\lvert a_{i.i} \rvert}\lbrace \substack{\le \: 1 \: 對所有方程 \\ \lt \: 1 \: 至少對一個方程}}$$
這就是為什麼有時我們需要改變方程在陣列中的順序以實現所謂的對角佔優的原因。
讓我們透過以下示例來演示演算法：
$$\mathrm{20x \: + \: y \: − \: 2z \: = \: 17}$$
$$\mathrm{3x \: + \: 20y \: − \: z \: = \: −18}$$
$$\mathrm{2x \: − \: 3y \: + \: 20z \: = \: 25}$$
將上述方程重新排列如下：
$$\mathrm{x_{new} \: = \: (−y_{guess} \: + \: 2z_{guess} \: + \: 17)/20}$$
$$\mathrm{y_{new} \: = \: (−3x_{guess} \: + \: z_{guess} \: − \: 18)/20}$$
$$\mathrm{z_{new} \: = \: (−2x_{guess} \: + \: 3y_{guess} \: + \: 25)/20}$$
現在，這些方程將在while迴圈中求解，以根據猜測值和當前獲得的值獲得未知數的新值。
模擬高斯-塞德爾方法的Python程式
實現高斯-塞德爾方法（按方程實現）的程式如下所示：
示例
# Importing modules
from pylab import *
from numpy import *
# Settingup initial guess
xg=0
yg=0
zg=0
#Error for entering in the loop
error=1
# Iteration counter
count=0
while error>1.E-5:
count+=1
x=(17-yg+2*zg)/20
y=(zg-18-3*x)/20 # Here x is x_new (obtained in this step only)
z=(25-2*x+3*y)/20 # Here x and y are x_new and y_new (obtained in this step only)
# Evaluating and Plotting the errors
error = abs(x-xg)+abs(y-yg)+abs(z-zg)
figure(1,dpi=300)
semilogy(count,error,'ko')
xlabel('iterations')
ylabel('error')
# Setting the guess for the next iteration
xg=x
yg=y
zg=z
savefig('error_GS.jpg')
print(f'x={round(x,5)}, y={round(y,5)}, z={round(z,5)}')
輸出
程式輸出將是
$$\mathrm{x \: = \: 1.0 \: , \: y \: = \: −1.0 \: , \: z \: = \: 1.0}$$
但需要注意的關鍵是誤差圖，從中可以清楚地看出，收斂解僅在五步之後就達到了。
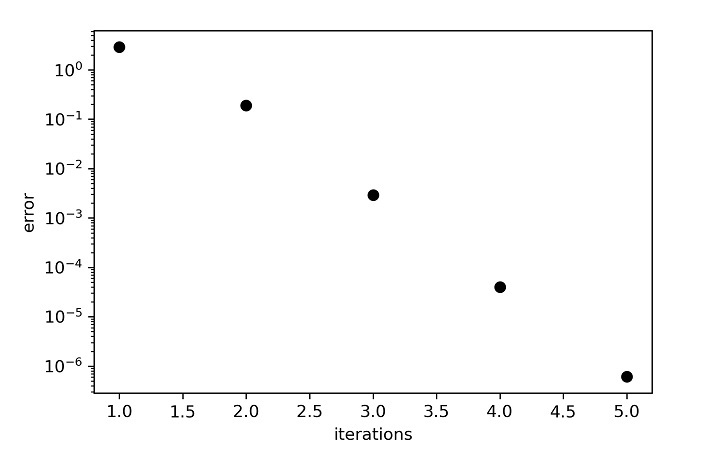
當方程的數量變大時，對我們來說，編寫方程並在迴圈中求解就變得非常困難。因此，為了處理這個困難，係數被捆綁在一個矩陣中，可以很容易地將其插入到程式中。高斯-塞德爾實現的矩陣方法如下：
示例
# Importing modules
from pylab import *
from numpy import *
# Coefficient matrix
a=array([[20,1,-2],[3,20,-1],[2,-3,20]])
# RHS vector
b=array([17,-18,25])
# Number of rows and columns in matrix
n=len(b)
# Settingup the initial guess
xn=zeros(len(b))
# Setting error to move in loop
error=1
# Settin iteration counter
count=0
# copying guess array to new
xg=xn.copy()
while error>1.E-5:
count+=1
for i in range(n):
sum1=0
for j in range(n):
if i!=j:
sum1=sum1+a[i,j]*xn[j]
xn[i]=(-1/a[i,i])*(sum1-b[i])
# Evaluating and plotting error
error = sum(abs(xn-xg))
figure(1,dpi=300)
semilogy(count,error,'ko')
xlabel('iterations')
ylabel('error')
# Updating guess
xg=xn.copy()
savefig('error_GS1.jpg')
print('x: ',xn)
輸出
程式輸出將是
$$\mathrm{x \: : \: 0.99999999 \: , \: −1 \: , \: 1}$$
結論
在本教程中，我們嘗試對著名的Gauss-Seidel方法進行建模。已經介紹了該方法的深入演算法。我們還解決了一個示例問題並給出了誤差圖。
高斯-塞德爾方法的成功在於方程的編寫方式。如果系統是對角佔優的，那麼可以確保獲得正確的答案，否則必須重新排列方程。
2K+ 瀏覽量
