資料結構
網路
關係資料庫管理系統
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理學
化學
生物學
數學
英語
經濟學
心理學
社會學
服裝設計
法律研究Python 中穩態流動能量方程建模
穩態流動能量方程 (SFEE) 是能量守恆定律在開放系統中的應用。下圖是開放系統的示意圖，其中流體從 𝑖 進入，從 𝑒 出口。紅色虛線表示控制體積 (CV) 的控制面 (CS)。
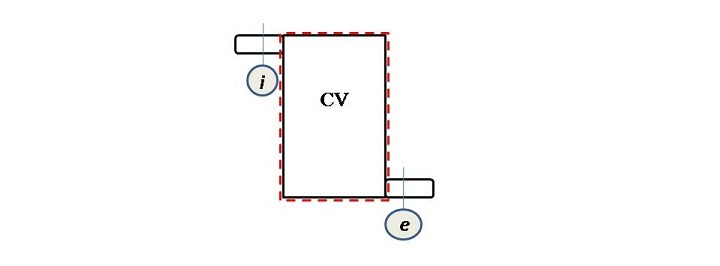
入口和出口引數如下表所示：
| 引數 | 入口 | 出口 |
|---|---|---|
| 壓力 | pi | pe |
| 速度 | Vi | Ve |
| 密度 | Pi | Pe |
| 比容 | vi | ve |
| 焓 | hi | he |
| 面積 | Ai | Ae |
| 基準面 | zi | ze |
對於單個輸入和輸出系統（如上所示），SFEE 可以寫成：
$$\mathrm{\dot{E}_I+\dot{Q}=\dot{E}_e+\dot{W}_{shaft}}$$
其中，$\mathrm{\dot{Q}}$ 和 $\mathrm{\dot{W}_{shaft}}$ 代表傳給 CV 的 CS 的熱傳遞速率和從 CV 的 CS 輸出的軸功。$\mathrm{\dot{E}_𝑖}$ 和 $\mathrm{\dot{E}_𝑒}$ 表示隨著質量流入和流出 CV 的能量。等式 1 的展開形式顯示在等式 2 中。
$$\mathrm{\dot{m}_I(h_i+\frac{v^{2}_i}{2}+gzi)+\dot{m}=m_e(h_e+\frac{v^{2}_e}{2}+gz_e)\dot{W}_{shaft}}$$
公式 1 和 2 適用於單個輸入和輸出，但如果存在多個輸入輸出以及多個熱相互作用，則公式變為：
$$\mathrm{\sum \dot{E}_I+\sum\dot Q=\sum \dot{E}_e+\dot{W}_{Shaft}}$$
$$\mathrm{\sum(\dot{m}_I(h_i+\frac{v^{2}_i}{2}+))+\sum\dot Q=\sum(\dot{m}_e(h_e+\frac{v^{2}_e}{2}+gze))+\dot{W}_{shaft}}$$
除了這些方程之外，還需要求解質量守恆。事實上，必須先求解質量守恆，然後再求解能量方程。因此，對於多輸入輸出控制體積，進入系統的淨質量應等於離開系統的淨質量。
$$\mathrm{\sum m_i=\sum m_e}$$
沒有直接的方法可以在 Python 中對上述方程進行建模，因此，將根據手頭的具體問題進行建模。我們將建立一個程式的 case 型別結構，在其中為方程中每個缺失的條目建立函式。
以下函式是為單個入口和出口開發的：
用於計算焓
def Enthaply(T,c): """ Enter temperature in deg C """ return c*(T+273)
排放/質量流量
def mass_flow(ρ,a,v): return ρ*a*v
入口焓
def SFEE_hi(he,vi,ve,zi,ze,Q,W,mi,me): """ h: in kJ/kg v: m/s z: m/s Q: kW W: kW m: kg/s """ return (me*(he+1.E-3*ve**2/c+1.E-3*g*ze)+W-Q)/mi-(1.E-3*vi**2/2+1.E3*g*zi)
出口焓
def SFEE_he(hi,vi,ve,zi,ze,Q,W,mi,me): """ h: in kJ/kg v: m/s z: m/s Q: kW W: kW m: kg/s """ return (mi*(hi+1.E-3*vi**2/2+1.E-3*g*zi)-W+Q)/me-(1.E-3*ve**2/2+1.E3*g*ze)
熱傳遞
def SFEE_Q(hi,he,vi,ve,zi,ze,W,mi,me): """ h: in kJ/kg v: m/s z: m/s W: kW m: kg/s """ return me*(he+1.E-3*ve**2/2+1.E-3*g*ze)-mi*(hi+1.E-3*vi**2/2+1.E3*g*zi)+W
軸功
def SFEE_W(hi,he,vi,ve,zi,ze,Q,mi,me): """ h: in kJ/kg v: m/s z: m/s Q: kW m: kg/s """ return mi*(hi+1.E-3*vi**2/2+1.E-3*g*zi)-me*(he+1.E-3*ve**2/2+1.E3*g*ze)+Q
入口速度
def SFEE_vi(hi,he,ve,zi,ze,Q,W,mi,me): """ h: in kJ/kg v: m/s z: m/s Q: kW W: kW m: kg/s W: kW """ a= (me*(he+1.E-3*ve**2/2+1.E-3*g*ze)+W-Q)/mi return sqrt(2000*(a-(hi+1.E-3*g*zi)))
出口速度
def SFEE_ve(hi,he,vi,zi,ze,Q,W,mi,me): """ h: in kJ/kg v: m/s z: m/s Q: kW W: kW m: kg/s W: kW """ a= (mi*(hi+1.E-3*vi**2/2+1.E-3*g*zi)-W+Q)/me return sqrt(2000*(a-(he+1.E-3*g*ze)))
讓我們舉幾個例子來演示這些函式的使用。
示例 1
在一個絕熱噴嘴中，入口和出口壓力分別為 31 巴和 1 巴，入口溫度為 527°C。氣體的比熱為 1 kJ/kg-K，𝛾 = 1.4。如果入口速度可以忽略不計，則估計出口速度。
解決方案：在這種情況下，我們首先必須計算出口溫度。由於噴嘴是絕熱的，因此出口溫度將計算為：
$$\mathrm{T_2=(\frac{p_2}{p_1})^{\frac{y-1}{y}}}$$
此外，由於這是噴嘴，所以：$\mathrm{ 𝑊 = 0, z_i = z_e = 1.0, m_i = m_e=1.0}$
此問題的 Python 程式碼如下：
from math import *
# Adiabatic exponent
γ=1.4
# Specific heat
c= 1
# Heat and work
Q=W=0
# Inlet temperature and pressure
Ti = 800
pi = 31
# Exit pressure
pe = 1
# datum at inlet and exit
zi=ze=1
# mass flow rate at inlet and exit
mi=me=1
# velocity at inlet
vi=0
# Evaluating exit temperature based on adiabatic condition
Te=Ti*(pe/pi)**(1-1/γ) # in Kelvin
# Evaluating inlet and exit enthalpy
hi=Enthaply(Ti,c)
he=Enthaply(Te,c)
# Calling function to evaluate exit velocity
Ve=SFEE_ve(hi,he,vi,zi,ze,Q,W,mi,me)
print(f"Ve = {round(Ve,3)} m/s")
程式的輸出將為：
Ve = 1000.093 m/s
示例 2
空氣 (𝑅 = 0.287 kJ/kg-K，$\mathrm{c_p}$ = 1.005 kJ/kg-K，和 𝛾 = 1.4) 依次流過壓縮機、加熱器和渦輪機，如圖所示。當壓力和溫度分別為 276 kPa 和 316 K 時，從壓縮機出來的空氣的體積流量為 2.33 $\mathrm{m^3/s}$。然後在加熱器中以相同的壓力將空氣加熱到 703 K。從加熱器中，空氣流過一個產生 1860 kW 功率的渦輪機。從渦輪機到周圍環境的熱損失為 90 kW。渦輪機出口處的空氣溫度（K）是多少？
解決方案 - 壓縮機出口處的排放量 = 2.33 $\mathrm{m^3/s}$，$\mathrm{𝑝_1}$ = 276 kPa，$\mathrm{𝑇_1}$ = 316 K，$\mathrm{𝑝_2}$ = 276 kPa，$\mathrm{𝑇_2}$ = 703 K，$\mathrm{𝑊_𝑡}$ = 1860 kW，$\mathrm{𝑄_𝑡}$ = 90 kW。在此問題中，由於沒有提及速度和基準面，因此我們將認為它們可以忽略不計。
由於這是一個穩態問題，因此我們必須首先根據壓縮機的出口條件找到質量流量，並直接檢視渦輪機並計算出口焓，最後計算溫度。
此問題的 Python 程式如下：
from math import *
# Adiabatic exponent
γ=1.4
# Specific heat
c= 1.005
# Characteristic gas const.
R=0.287
# Data at compressor exit
disc =2.33 #m^3/s
p1=276 #kPa
T1=316 #K
# Data at heater exit
p2=276 #kPa
T2=703 #K
# Data for turbine
Wt=1860 #kW
Qt=-90 #kW.
# Evaluating mass flow rate
ρ1=p1/(R*T1)
m=ρ1*disc
# Enthalpy at heater exit
h2=Enthaply(T2,c)
# Velocity and pressure at Turbine exit and inlet
v2=v3=0
z2=z3=0
# obtaining enthalpy at turbine exit
h3=SFEE_he(h2,v2,v3,z2,z3,Qt,Wt,m,m)
# Temperature at turbine exit
T3=h3/c
print(f'T3 = {round(T3,3)} K')
程式的輸出將為：
T3 = 429.364 K
結論
在本教程中，已在 Python 中對穩態流動能量方程進行了建模。開發了不同的函式，並透過兩個示例展示了其實現。
154 次檢視
