使用Python建模二維熱傳導問題
在本教程中,我們將學習如何使用Python模擬二維熱傳導方程。帶有熱生成的二維穩態熱傳導方程可以用笛卡爾座標表示如下:
$$\mathrm{\triangledown^{2} T \: + \: \frac{q_{g}}{k} \: = \: \frac{\partial^{2}T}{\partial x^{2}} \: + \: \frac{\partial^{2}T}{\partial y^{2}} \: + \: \frac{q_{g}}{k} \: = \: 0 \:\:\dotso\dotso (1)}$$
這需要離散化才能得到有限差分方程。讓我們考慮如下所示的矩形網格。

索引𝑖垂直執行,即行方向,而索引𝑗水平執行,即列方向。任何內部節點(i,j)都被四個節點包圍,因此該節點的資訊只能從這四個節點傳輸。而對於邊界節點,資訊將來自邊界條件。
為了離散化方程1,將使用二階精度的中心差分格式。此外,水平方向和垂直方向的網格點間距保持相同,即$\mathrm{\Delta x \: = \: \Delta y \: = \: \Delta}$。單變數函式二階導數的中心差分公式為:
$$\mathrm{\frac{d^{2}f(x)}{dx^{2}} \: = \: \frac{f_{i-1} \: − \: 2f_{i} \: + \: f_{i+1}}{\Delta x^{2}}\:\:\dotso\dotso (2)}$$
同樣,方程1的離散化可以寫成:
$$\mathrm{\frac{T_{i-1, \: j} \: − \: 2T_{i,\: j} \: + \: T_{i+1, \: j}}{\Delta x^{2}} \: + \: \frac{T_{i, \: j-1} \: − \: 2T_{i,\: j} \: + \: T_{i, \: j+1}}{\Delta 6^{2}} \: + \: \frac{q_{g}}{k} \: = \: 0 \:\:\dotso\dotso (3)}$$
方程3的簡化形式為:
$$\mathrm{T_{i,\: j} \: = \: \frac{1}{4}(T_{i-1, \: j}\: + \: T_{i+1, \: j} \: + \: T_{i,\: j-1} \: + \: T_{i, \: j+1} \: + \: \Delta^{2} \frac{q_{g}}{k}) \:\:\dotso\dotso (4)}$$
方程4是必須針對域中每個內部節點求解的方程。
對於這類問題,資訊從邊界傳播到內部,因此邊界條件的知識至關重要。基本上,在任何數值和分析分析中經常使用三種類型的邊界條件:
狄利克雷邊界條件:在此條件下,邊界上因變數的值已知。例如
$$\mathrm{x \: = \: 0 \: \rightarrow \: T \: = \: 500 \: K }$$
諾依曼邊界條件:在此條件下,因變數的導數給出為零或自變數的函式。例如
$$\mathrm{x \: = \: 0 \: \rightarrow \: \frac{\partial T}{\partial x} \: = \: 0 }$$
羅賓邊界條件:在此條件下,因變數的導數是因變數本身的某個函式。例如
$$\mathrm{− \: k \: (\frac{\partial T}{\partial x})_{x=0} \: = \: h(T \: − \: T_{\infty}) }$$
演算法
選擇區域
選擇x和y方向的網格點數
定義$\mathrm{\Delta x}$和$\mathrm{\Delta y}$。
定義網格。
提供溫度的初始猜測值。
提供邊界條件
對方程4中的內部節點求解
評估誤差。
如果誤差大於收斂標準,則將當前T值設定為新的猜測值,並遵循步驟4-9。否則,答案已達到,並繪製結果。
在本教程中,我們將解決兩種情況,即有熱量產生和無熱量產生。此外,我們將假設狄利克雷邊界條件。
待解決的問題如下:
問題1

問題2

對於這兩個問題,除了熱量產生引數外,其他所有引數都保持不變。這就是為什麼本文只顯示一次程式碼的原因。
Importing modules
from pylab import *
from numpy import*
# Defining thermal properties
# case 1
# qg=0
# case 2
qg= 1000000
k=100
# Define domain
ℓx=1.0
ℓy=1.0
# Number of grid points
nx=20
ny=20
# Grid spacing
Δx=ℓx/(nx-1)
Δy=ℓy/(ny-1)
Δ=Δx
# Grid generation
x=linspace(0,ℓx,nx)
y=linspace(0,ℓy,ny)
X,Y=meshgrid(x,flipud(y))
# Initial Guess
T=zeros(shape=(nx,ny))
# Boundary conditions
#left
T[:,0]=300
#right
T[:,-1]=300
#top
T[0,:]=800
#bottom
T[-1,:]=300
# Guess array for comparison
Tg=T.copy()
# Initial error or entry in loop
error=1
# Iteration counter
count=1
# Comparison loop
while error>1.E-5:
# Sweeping in the domain
for i in range(1,nx-1):
for j in range(1,ny-1):
T[i,j]=(T[i,j-1]+T[i,j+1]+T[i-1,j]+T[i+1,j]+Δ**2*qg/k)/4
# Evaluating and printing error
error=sqrt(sum(abs(T-Tg)**2))
figure(1,dpi=300)
if count%100==0:
print(error)
semilogy(count,error,'ko')
xlabel("Iteration Counter")
ylabel("Error")
savefig("Error.jpg")
# Updating guess for next iteration
Tg=T.copy()
# Incrementing counter
count+=
# Result Plotting (Temperature contour plot)
figure(3,dpi=300)
cp1=contourf(X,Y,T,10,cmap='jet')
colorbar()
cp1=contour(X,Y,T,10,colors='k')
clabel(cp1,inline=True, fontsize=10)
savefig("temp.jpg")
第一種情況的誤差和溫度圖


第二種情況的誤差和溫度圖

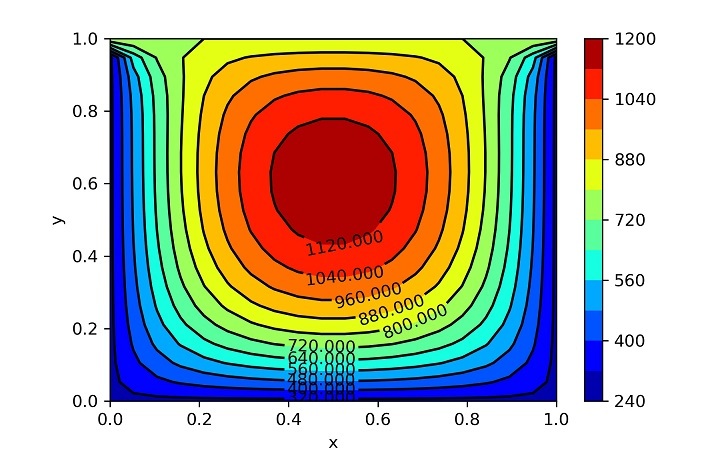
現在您可以觀察到,熱量的產生導致核心溫度升高,以至於邊界條件的影響無法與之匹配。在問題一中,您觀察到影響從頂部開始,向底部和側面移動。然而,在第二種情況下,邊界條件試圖施加影響,但是由於熱量產生過高,熱流的方向現在從中心向外移動。然而,由於問題必須匹配邊界條件,因此邊界溫度保持不變。
結論
在本教程中,二維熱傳導方程已在Python中建模。有限差分法已被用於解決兩個問題:一個是有熱量產生,另一個是無熱量產生。已經觀察到,程式碼中採用的熱量產生大小對最終穩態解的影響不大。


 資料結構
資料結構 網路
網路 關係資料庫管理系統 (RDBMS)
關係資料庫管理系統 (RDBMS) 作業系統
作業系統 Java
Java iOS
iOS HTML
HTML CSS
CSS Android
Android Python
Python C語言程式設計
C語言程式設計 C++
C++ C#
C# MongoDB
MongoDB MySQL
MySQL Javascript
Javascript PHP
PHP