Python 中的割線法建模
割線法是用於求解多項式或任何超越函式的 x 截距(零點)的強大方法之一。在這種方法中,我們首先選擇(基本上是猜測)我們期望根所在的區間($\mathrm{𝑥_{1}}$,$\mathrm{𝑥_{2}}$)。然後,我們繪製一條割線以連線對應於猜測值的函式上的點(A,B),如下圖所示。
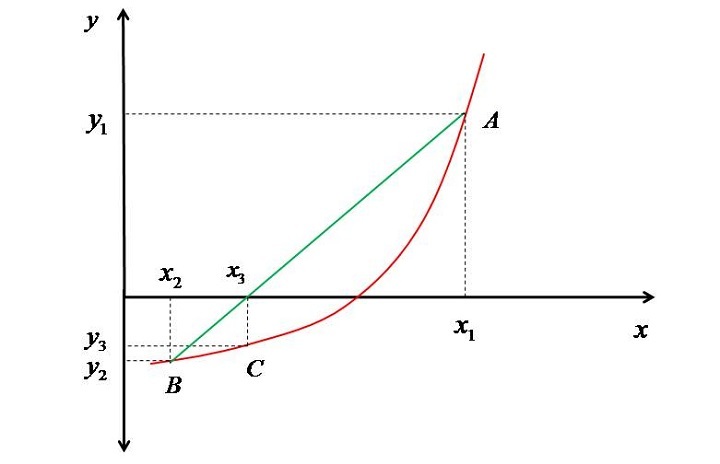
割線與 x 軸相交於點 $\mathrm{𝑥_{3}}$,由於 $\mathrm{𝑥_{3}}$ 和 $\mathrm{𝑥_{2}}$ 不接近(即它們的絕對差是有限的),我們找到對應於 $\mathrm{𝑥_{3}}$ 曲線上的點,即 C。然後,我們考慮點 B 和 C 連線一條割線。我們將這條線延伸到到達 X 軸,並將該點標記為 $\mathrm{𝑥_{4}}$。
現在,我們再次檢查 $\mathrm{𝑥_{3}}$ 和 $\mathrm{𝑥_{4}}$ 是否接近。由於它們也不接近,因此我們找到對應於 $\mathrm{𝑥_{4}}$ 的多項式的值,並在曲線上將其標記為 D。下圖表示第二條割線和點 D。
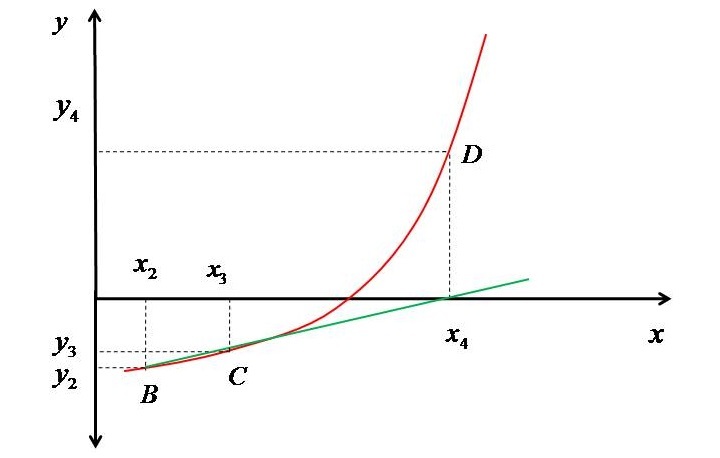
然後,我們再次在 C 和 D 之間繪製一條割線,直到“x”的下一個值和前一個值的距離收斂到一個非常小的值。因此,我們可以說該方法依次找到多項式的根,即它可以被認為是根的順序搜尋。這種方法的優點在於,x 是否位於根的一側或圍繞根並不重要。該方法透過上述解釋的順序搜尋逐漸收斂到根。
現在,任務是根據前兩個 x 來評估下一個 x。如果我們考慮第一條割線,那麼透過它們(以評估 $\mathrm{𝑥_{3}}$)的直線方程如下:
$$\mathrm{x_{3}=x_{1}-y_{1}\frac{x_{2}-x_{1}}{y_{2}-y_{1}}}$$
而如果我們考慮第二條割線,則用於評估的直線方程如下:
$$\mathrm{x_{4}=x_{2}-y_{2}\frac{x_{3}-x_{2}}{y_{3}-y_{2}}}$$
因此,上述方程的廣義版本如下:
$$\mathrm{x_{i}=x_{i-2}-y_{i-2}\frac{x_{i-1}-x_{i-2}}{y_{i-1}-y_{i-2}}}$$
Python 中的割線法實現
可以使用以下演算法對割線法進行建模:
首先需要定義需要求根的函式 f(x)
選擇兩個任意 x 值,即 ($\mathrm{𝑥_{1}}$,$\mathrm{𝑥_{2}}$)
使用以下公式評估 x 的新值 $$\mathrm{x_{n}=x_{1}-f(x_{1})\frac{x_{2}-x_{1}}{f(x_{2})-f(x_{1})}}$$
如果 x 的新值和前一個值接近,則得到答案,即如果 $|x_{n_{}}-x2|<10^{-5}$,則 $𝑥_{𝑛}$ 是根。注意,我們取收斂準則為 $10^{-5}$,但您可以根據您的需要進行設定。
如果 $|x_{n_{}}-x2|>10^{-5}$,則設定:$𝑥_{1}$=$𝑥_{2}$ 和 $𝑥_{2}$=$𝑥_{𝑛}$
然後再次從評估新 x 的步驟開始。
然後再次從評估新 x 的步驟開始。
假設我們想要找到方程:$𝑥^{2}$+3𝑥−10=0 的根。讓我們選擇初始值為 ($𝑥_{1}$=−4,$𝑥_{2}$= 3)。然後執行割線法的 Python 程式如下:
# Importing module
from pylab import *
# Defining Polynomial function
def f(x):
return x ** 2 + 3 * x - 10
# Defining function for new value of x
def fn(a, b):
return a - ((b - a) / (f(b) - f(a))) * f(a)
# Creating array of x
x = linspace(-15, 15, 150)
# Plotting the function
figure(1, figsize=(7.20, 3.50))
plot(x, f(x), linewidth=2)
plot([-25, 25], [0, 0], "k--")
ylim(-15, 20)
xlim(-8, 6)
# Initial guess Interval
x1 = -4
x2 = 3
# Initial Error to enter into the loop
error = 1
# Setting iteration counter
count = 1
# Integration starts
while error > 1.E-3:
# Plotting Secant line
plot([x1, x2], [f(x1), f(x2)])
# Evaluating new value of x based on old
xn = fn(x1, x2)
# Plotting x intercept of secant
plot([xn], [0], 'o', label=f'{xn}')
# Evaluating error
error = abs(x2 - xn)
# Setting x's for next iteration
x1 = x2
x2 = xn
# Incrementing loop counter
count += 1
# Printing selected value of xn in the legend
if count < 6:
legend()
# Showing root in the figure (just decoration)
text(-7, -10, f'Root = {round(xn, 3)}', bbox={'facecolor': 'red', 'alpha': 0.5, 'pad': 10})
print(f'Root = {round(xn, 3)}')
show()
上述程式碼清楚地說明了本節開頭提到的所有步驟。上述程式的輸出將如以下圖所示。
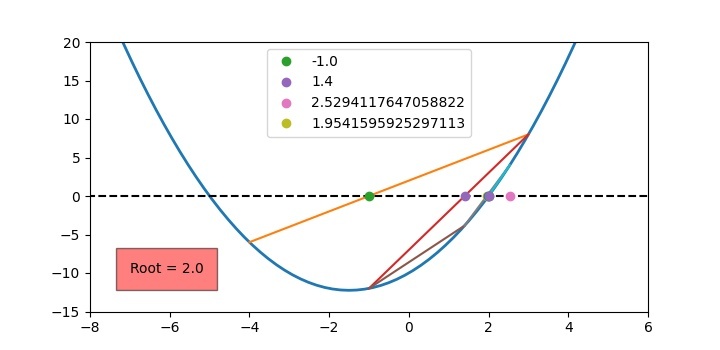
對於其他根,您可以將初始“x”取為:−6 和 −2。然後結果如下所示
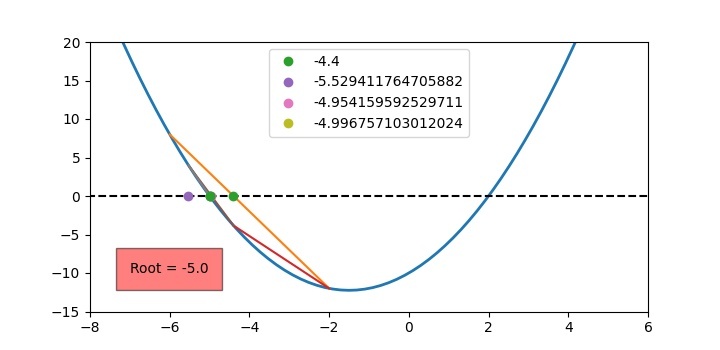
結論
本文詳細討論了割線法。給出了數學背景,以便輕鬆地對該方法進行建模。使用者可以修改上面給出的程式碼,並使用它來查詢其他函式的根。


 資料結構
資料結構 網路
網路 關係型資料庫管理系統
關係型資料庫管理系統 作業系統
作業系統 Java
Java iOS
iOS HTML
HTML CSS
CSS Android
Android Python
Python C 語言程式設計
C 語言程式設計 C++
C++ C#
C# MongoDB
MongoDB MySQL
MySQL Javascript
Javascript PHP
PHP