資料結構
網路
關係型資料庫管理系統 (RDBMS)
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C語言程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理學
化學
生物學
數學
英語
經濟學
心理學
社會學
時尚研究
法學研究Python中的奧托迴圈和柴油迴圈建模
奧托迴圈
奧托迴圈是一種用於火花點火 (SI) 發動機的空氣標準迴圈。它包括兩個可逆絕熱過程和兩個等容過程（恆容），共四個過程。當功相互作用發生在可逆絕熱過程中時，熱量增加 (2-3) 和減少 (4-1) 發生在等容過程中 (3-4 和 1-2)。奧托迴圈示意圖如下所示。
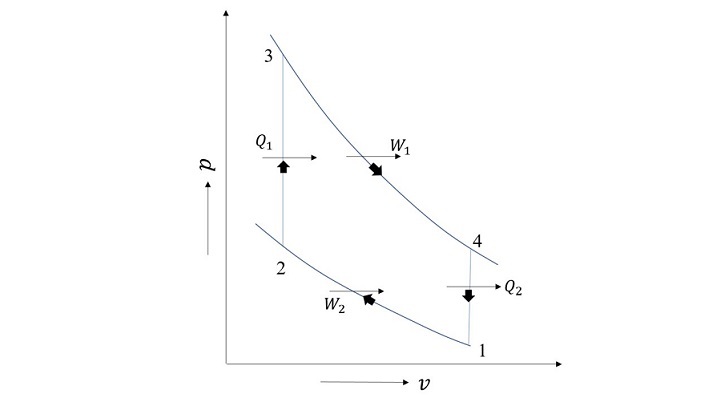
為了在 Python 中模擬該迴圈，考慮的輸入變數是最大壓力 $\mathrm{(P_{max})}$、最小壓力 $\mathrm{(P_{min})}$、最大容積 $\mathrm{(V_{max})}$、壓縮比 (r) 和絕熱指數 $\mathrm{(\gamma)}$。表 2 解釋了奧托迴圈中不同過程的熱力學計算：
過程 1-2
$$\mathrm{p_{1} \: = \: p_{min}}$$
$$\mathrm{v_{1} \: = \: v_{max}}$$
使用壓縮比 (𝑟)，首先根據點 1 處的體積計算點 2 處的體積：
$$\mathrm{v_{2} \: = \: \frac{v_{1}}{r}}$$
然後計算過程 1-2 的絕熱常數：
$$\mathrm{c_{1} \: = \: p_{1} \: \times \: v_{1}^{\gamma}}$$
一旦已知 $\mathrm{c_{1}}$，則沿線 1-2 的壓力變化計算為：
$$\mathrm{p \: = \: \frac{c_{1}}{v^{\gamma}}}$$
過程 2-3
$$\mathrm{p_{3} \: = \: p_{max}}$$
由於該過程是等容的，因此體積保持不變：
$$\mathrm{v_{3} \: = \: v_{2}}$$
因此，點 2 處的壓力可以計算為：
$$\mathrm{p_{2} \: = \: \frac{c_{1}}{v^{\gamma}_{2}}}$$
過程 3-4
設 $\mathrm{c_{2}}$ 為沿線 3-4 的常數。由於已知點 3 處的壓力和溫度，因此沿可逆絕熱線的常數可以計算為：
$$\mathrm{c_{2} \: = \: p_{3} \: \times \: v_{3}^{\gamma}}$$
並且由於 $\mathrm{v_{4} \: = \: v_{1}}$，因此沿 3-4 的壓力可以計算為：
$$\mathrm{p \: = \: \frac{c_{2}}{v^{\gamma}}}$$
過程 4-1
$\mathrm{c_{2}}$ 和 $\mathrm{c_{4}}$ 已知，因此 $\mathrm{p_{4}}$ 可以計算為
$$\mathrm{p_{4} \: = \: \frac{c_{4}}{v^{\gamma}_{4}}}$$
奧托迴圈的Python程式
奧托迴圈的 Python 函式如下所示：
from pylab import *
from pandas import *
def otto(p_min,p_max,v_max,r,gma):
font = {'family' : 'Times New Roman','size' : 39}
figure(figsize=(20,15))
rc('font', **font)
'''This function prints Otto cycle
arguments are as follows:
_min: minimum pressure
p_max: Maximum pressure
v_max: Maximum volume
r: compression ratio
gma: Adiabatic exponent
The order of arguments is:
p_min,p_max,v_max,r,gma
'''
#~~~~~~~~~~~~~~~~~~~~~~~~~
# Process 1-2
#~~~~~~~~~~~~~~~~~~~~~~~~~
p1=p_min
v1=v_max
v2=v1/r
c1=p1*v1**gma
v=linspace(v2,v1,100)
p=c1/v**gma
plot(v,p/1000,'b',linewidth=3)
#~~~~~~~~~~~~~~~~~~~~~~~~~
# Process 2-3
#~~~~~~~~~~~~~~~~~~~~~~~~~
p3=p_max
v3=v2
p2=c1/v2**gma
p=linspace(p2,p3,100)
v=100*[v3]
plot(v,p/1000,'r',linewidth=3)
#~~~~~~~~~~~~~~~~~~~~~~~~~
# Process 3-4
#~~~~~~~~~~~~~~~~~~~~~~~~~
c2=p3*v3**gma
v4=v1
v=linspace(v3,v4,100)
p=c2/v**gma
plot(v,p/1000,'g',linewidth=3)
#~~~~~~~~~~~~~~~~~~~~~~~~~
# Process 4-1
#~~~~~~~~~~~~~~~~~~~~~~~~~
v4=v1
p4=c2/v4**gma
p=linspace(p1,p4,100)
v=100*[v1]
plot(v,p/1000,'r',linewidth=3)
title('Otto Cycle',size='xx-large',color='k')
xlabel('Volume ($m^3$)')
ylabel('Pressure (kPa)')
text(v1,p1/1000-30,'1')
text(v2,p2/1000-200,'2')
text(v3+0.01,p3/1000-20,'3')
text(v4,p4/1000+10,'4')
data={'p':[p1,p2,p3,p4],
'v':[v1,v2,v3,v4],
'c':[c1,'' ,c2,'' ],
'State': [1,2,3,4]}
df=DataFrame(data)
savefig('Otto_final.jpg')
return df.set_index('State')
oc=otto(2*10**5,35*10**5,0.5,5,1.4)
show()
oc
對於 $\mathrm{p_{min} \: = \: 2 \: \times \: 10^{5} \: Pa \: , \: p_{max} \: = \: 35 \: \times \: 10^{5} \: Pa \: , \: v_{max} \: = \: 0.5 \: m^{3} \: , \: r \: = \: 5 \: and \: \gamma \: = \: 1.4 \: ,}$ 程式生成的奧托迴圈圖如下所示：
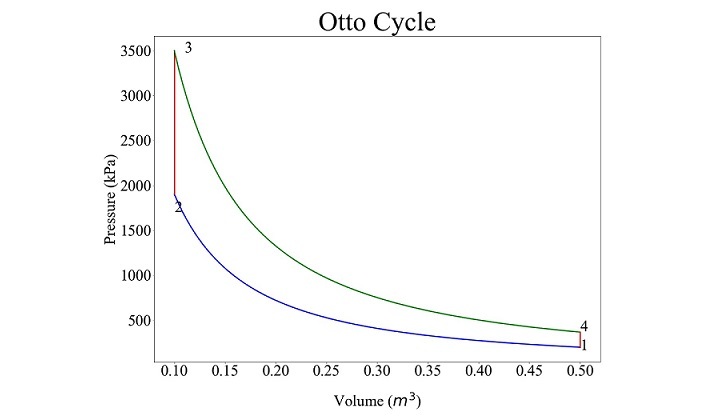
從程式碼中獲得的不同點的壓力和體積如下：
狀態 |
p |
v |
|---|---|---|
1 |
2.000000e+05 |
0.5 |
2 |
1.903654e+06 |
0.1 |
3 |
3.500000e+06 |
0.1 |
4 |
3.677139e+05 |
0.5 |
柴油迴圈
柴油迴圈是壓縮點火 (CI) 發動機中使用的空氣標準迴圈。該迴圈由四個過程組成：兩個可逆絕熱過程、一個等壓過程（恆壓）和兩個等容過程（恆容）。熱量增加發生在過程 2-3，而熱量減少發生在過程 4-1。過程 1-2 和 3-4 分別是功相互作用進入和離開迴圈的過程。柴油迴圈圖如下所示。
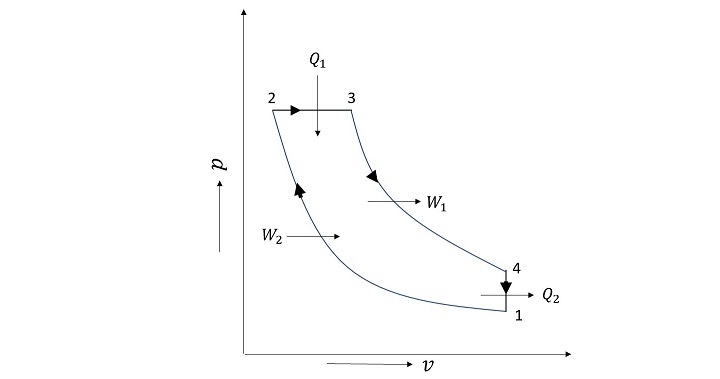
為了模擬該迴圈，考慮的輸入變數是最大壓力 $\mathrm{(p_{max})}$、最小壓力 $\mathrm{(p_{min})}$、最大容積 $\mathrm{(v_{max})}$、截止比 $\mathrm{(r_{c})}$ 和絕熱指數 \mathrm{(\gamma)}。下面解釋了柴油迴圈中不同過程的熱力學計算：
過程 1-2
$$\mathrm{p_{1} \: = \: p_{min}}$$
$$\mathrm{v_{1} \: = \: v_{max}}$$
$$\mathrm{p_{2} \: = \: p_{max}}$$
由於 1-2 是絕熱過程，因此遵循 $\mathrm{pv^{\gamma} \: = \: const \: ;}$ 設常數為 $\mathrm{(c_{1})}$。點 2 處的體積可以計算為：
$$\mathrm{v_{2} \: = \: v_{1} \: \times (\frac{p_{1}}{p_{2}})^{\frac{1}{\gamma}}}$$
因此 $\mathrm{c_{1} \: = \: p_{1} \: \times \: v_{1}^{\gamma}}$
然後計算過程 1-2 的絕熱常數：
$$\mathrm{c_{1} \: = \: p_{1} \: \times \: v_{1}^{\gamma}}$$
一旦已知 $\mathrm{c_{1}}$，則沿線 1-2 的壓力變化計算為：
$$\mathrm{p \: = \: \frac{c_{1}}{v^{\gamma}}}$$
過程 2-3
由於該過程是等壓的，因此壓力保持不變：
$$\mathrm{p_{3} \: = \: p_{2}}$$
點 3 處的體積可以計算為：
$$\mathrm{v_{3} \: = \: r_{c} \: \times \: v_{2}}$$
因此，可以很容易地知道體積 $\mathrm{v_{2}}$ 和 $\mathrm{v_{3}}$ 之間的壓力變化。
過程 3-4
設 $\mathrm{c_{2}}$ 為沿線 3-4 的常數。由於已知點 3 處的壓力和溫度，因此沿可逆絕熱線的常數可以計算為：
$$\mathrm{c_{2} \: = \: p_{3} \: \times \: v_{3}^{\gamma}}$$
並且由於 $\mathrm{v_{4} \: = \: v_{1}}$，因此沿 3-4 的壓力變化可以計算為：
$$\mathrm{p \: = \: \frac{c_{2}}{v^{\gamma}}}$$
過程 4-1
$\mathrm{c_{2}}$ 和 $\mathrm{v_{4}}$ 已知，因此 $\mathrm{p_{4}}$ 可以計算為
$$\mathrm{p_{4} \: = \: \frac{c_{4}}{v^{\gamma}_{4}}}$$
用於模擬柴油迴圈的Python程式
用於模擬柴油迴圈的 Python 函式如下所示：
#~~~~~~~~~~~~~~~~~~~
# Diesel Cycle
#~~~~~~~~~~~~~~~~~~~
def diesel(p_min,p_max,v_max,r_c,gma):
font = {'family' : 'Times New Roman','size' : 39}
figure(figsize=(20,15))
title('Rankine Cycle with Feed water heating (T-s Diagram)',color='b')
rc('font', **font)
'''This function prints Diesel cycle
arguments are as follows:
p_min: minimum pressure
p_max: Maximum pressure
v_max: Maximum volume
rc: Cut-Off ratio
gma: Adiabatic exponent
The order of arguments is:
p_min,p_max,v_max,rc,gma
'''
#~~~~~~~~~~~~~~~~~~~~~~~~~
# Process 1-2
#~~~~~~~~~~~~~~~~~~~~~~~~~
p1=p_min
v1=v_max
p2=p_max
v2=v1*(p1/p2)**(1/gma)
c1=p1*v1**gma
v=linspace(v2,v1,100)
p=c1/v**gma
plot(v,p/1000,'b',linewidth=3)
#~~~~~~~~~~~~~~~~~~~~~~~~~
# Process 2-3
#~~~~~~~~~~~~~~~~~~~~~~~~~
p3=p2
p=zeros(100)
p=p+p2
v3=r_c*v2
v=linspace(v2,v3,100)
plot(v,p/1000.,'r',linewidth=3)
#~~~~~~~~~~~~~~~~~~~~~~~~~
# Process 3-4
#~~~~~~~~~~~~~~~~~~~~~~~~~
v4=v1
c2=p3*v3**gma
v=linspace(v3,v4,100)
p=c2/v**gma
plot(v,p/1000,'g',linewidth=3)
#~~~~~~~~~~~~~~~~~~~~~~~~~
# Process 4-1
#~~~~~~~~~~~~~~~~~~~~~~~~~
v4=v1
v=100*[v4]
p4=c2/v4**gma
p=linspace(p1,p4,100)
plot(v,p/1000.,'m',linewidth=3)
title('Diesel Cycle',size='xx-large',color='b')
xlabel('Volume ($m^3$)')
ylabel('Pressure (kPa)')
text(v1,p1/1000-30,'1')
text(v2-0.01,p2/1000,'2')
text(v3+0.01,p3/1000-20,'3')
text(v4,p4/1000+10,'4')
data={'p':[p1,p2,p3,p4],
'v':[v1,v2,v3,v4],
'c':[c1,'' ,c2,'' ],
'State': [1,2,3,4]}
df=DataFrame(data)
savefig('Diesel_final.jpg')
return df.set_index('State')
dc=diesel(2*10**5,20*10**5,0.5,2,1.4)
show()
dc
對於 $\mathrm{p_{min} \: = \: 2 \: \times \: 10^{5} \: Pa \: , \: p_{max} \: = \: 20 \: \times \: 10^{5} \: Pa \: , \: v_{max} \: = \: 0.5 \: m^{3} \: , \: r_{c} \: = \: 2 \: and \: \gamma \: = \: 1.4 \: ,}$ 獲得的結果如下面的圖所示
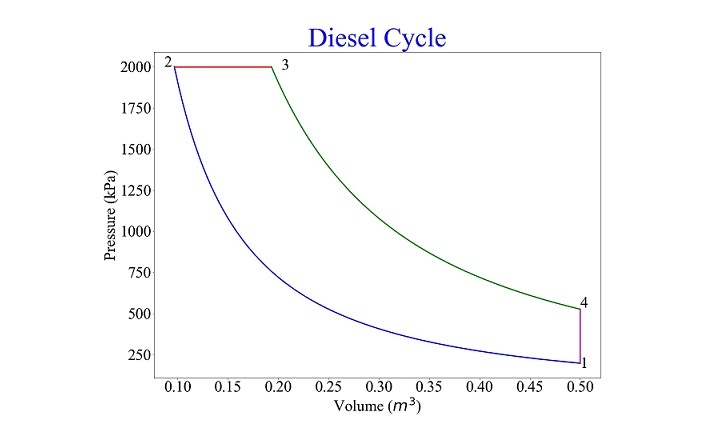
狀態 |
p |
v |
|---|---|---|
1 |
2.000000e+05 |
0.500000 |
2 |
2.000000e+06 |
0.096535 |
3 |
2.000000e+06 |
0.193070 |
4 |
5.278032e+05 |
0.500000 |
結論
在本教程中，藉助 Python 程式設計對奧托迴圈和柴油迴圈進行了建模。柴油和奧托迴圈的功能已程式設計和測試。該函式能夠根據輸入資料繪製迴圈。
333 次瀏覽
