
微波工程 - 傳輸線
傳輸線是一種聯結器,用於將能量從一點傳輸到另一點。傳輸線理論的研究有助於有效地利用電力和裝置。
基本上有四種類型的傳輸線:
- 雙線平行傳輸線
- 同軸線
- 帶狀基板傳輸線
- 波導
在傳輸或接收過程中,能量傳輸必須有效地進行,而不會浪費電力。為了實現這一點,必須考慮某些重要引數。
傳輸線的主要引數
傳輸線的重要引數包括電阻、電感、電容和電導。
電阻和電感一起稱為傳輸線阻抗。
電容和電導一起稱為導納。
電阻
傳輸線製作材料的電阻將相當大,特別是對於較短的線路。隨著線路電流的增加,歐姆損耗 (I²R 損耗) 也增加。
長度為“l”、橫截面積為“a”的導體的電阻R表示為
$$R = \rho \frac{l}{a}$$
其中
ρ = 導體材料的電阻率,為常數。
溫度和電流頻率是影響線路電阻的主要因素。導體的電阻隨溫度變化線性變化。而如果電流頻率增加,導體表面的電流密度也增加。否則,導體中心的電流密度增加。
這意味著,電流越嚮導體表面流動,向中心流動的電流就越少,這被稱為趨膚效應。
電感
在交流傳輸線中,電流呈正弦波變化。此電流感應出垂直於電場的磁場,該磁場也呈正弦波變化。這被稱為法拉第定律。下圖顯示了這些場。

這個變化的磁場在導體中感應出一些電動勢。現在,這個感應電壓或電動勢沿與最初流動的電流相反的方向流動。這個沿相反方向流動的電動勢等效地由一個稱為電感的引數表示,它是阻礙電流變化的特性。
用“L”表示。測量單位為“亨利(H)”。
電導
傳輸線與地之間以及相導線之間將存在漏電流。少量漏電流通常透過絕緣體的表面流動。此漏電流的倒數稱為電導。用“G”表示。
線路電流的流動與電感有關,兩點之間的電壓差與電容有關。電感與磁場有關,而電容與電場有關。
電容
相導線之間的電壓差導致導線之間產生電場。兩條導線就像平行板,它們之間的空氣成為電介質。這種模式導致導線之間產生電容效應。
特性阻抗
如果考慮均勻無損傳輸線,對於沿一個方向傳播的波,沿該線電壓和電流幅度的比率(沒有反射)稱為特性阻抗。
用 Z₀ 表示
$$Z_0 = \sqrt{\frac{電壓波值}{電流波值}}$$
$$Z_0 = \sqrt{\frac{R + jwL}{G + jwC}}$$
對於無損線路,R₀ = √(L/C)
其中 L & C 分別是單位長度的電感和電容。
阻抗匹配
為了將最大功率傳輸到負載,必須進行阻抗匹配。為了實現這種阻抗匹配,必須滿足以下條件:
負載電阻應等於電源電阻。
$$R_L = R_S$$
負載電抗應等於電源電抗,但符號相反。
$$X_L = -X_S$$
這意味著,如果電源是電感性的,則負載應是電容性的,反之亦然。
反射係數
表示由於傳輸線阻抗不匹配而產生的反射能量的引數稱為反射係數。用 ρ (rho) 表示。
它可以定義為“負載端子處反射電壓與入射電壓之比”。
$$\rho = \frac{反射電壓}{入射電壓} = \frac{V_r}{V_i} \: 在 \: 負載 \: 端子 \: 處$$
如果器件和傳輸線之間的阻抗不匹配,則能量會反射。反射能量越高,ρ 反射係數的值越大。
電壓駐波比 (VSWR)
當入射波反射時,會形成駐波。形成的駐波包含一些電壓。駐波的幅度可以用駐波比來衡量。
駐波中最大電壓與最小電壓之比可以定義為電壓駐波比 (VSWR)。用“S”表示。
$$S = \frac{\left |V_{max} \right |}{\left |V_{min} \right |} \quad 1\:\leq S \leq \infty$$
VSWR 描述了由於入射波和反射波的相加和相減而在傳輸線中存在的電壓駐波模式。
因此,它也可以寫成
$$S = \frac{1 + \rho }{1 - \rho }$$
阻抗失配越大,駐波的幅度就越高。因此,如果阻抗完全匹配,
$$V_{max} : V_{min} = 1:1$$
因此,VSWR 的值為 1,這意味著傳輸是完美的。
傳輸線的效率
傳輸線的效率定義為輸出功率與輸入功率之比。
傳輸線效率 % η = (接收端接收到的功率 / 從傳輸端傳送的功率) × 100
電壓調整率
電壓調整率定義為傳輸線傳送端和接收端電壓幅度的變化。
電壓調整率 % = (傳送端電壓 - 接收端電壓) / 傳送端電壓 × 100
由於阻抗不匹配造成的損耗
如果傳輸線沒有以匹配負載端接,則會發生損耗。這些損耗有多種型別,例如衰減損耗、反射損耗、傳輸損耗、回波損耗、插入損耗等。
衰減損耗
由於訊號在傳輸線中的吸收而發生的損耗稱為衰減損耗,表示為
$$衰減損耗 (dB) = 10 \: log_{10} \left [ \frac{E_i - E_r}{E_t} \right ]$$
其中
Eᵢ = 輸入能量
Eᵣ = 從負載反射到輸入的能量
Eₜ = 傳輸到負載的能量
反射損耗
由於傳輸線阻抗不匹配而導致訊號反射而發生的損耗稱為反射損耗,表示為
$$反射損耗 (dB) = 10 \: log_{10} \left [ \frac{E_i}{E_i - E_r} \right ]$$
其中
Eᵢ = 輸入能量
Eᵣ = 從負載反射的能量
傳輸損耗
在傳輸線傳輸過程中發生的損耗稱為傳輸損耗,表示為
$$傳輸損耗(dB) = 10 \: log_{10} \: \frac{E_i}{E_t}$$
其中
Eᵢ = 輸入能量
Eₜ = 傳輸的能量
回波損耗
傳輸線反射功率的度量稱為回波損耗,表示為
$$回波損耗(dB) = 10 \: log_{10} \: \frac{E_i}{E_r}$$
其中
Eᵢ = 輸入能量
Eᵣ = 反射能量
插入損耗
使用傳輸線進行能量傳輸與不使用傳輸線進行能量傳輸相比發生的損耗稱為插入損耗,表示為
$$插入損耗(dB) = 10 \: log_{10} \: \frac{E_1}{E_2}$$
其中
E₁ = 負載直接連線到電源時(無傳輸線)接收到的能量。
E₂ = 負載和電源之間連線傳輸線時負載接收到的能量。
阻抗匹配
如果負載阻抗與源阻抗不匹配,則有時使用稱為“阻抗匹配”的方法來實現匹配。
在某一點或多點處與主線並聯連線開路或短路線段(稱為阻抗匹配)的過程,可以稱為阻抗匹配。
在較高的微波頻率下,主要採用兩種阻抗匹配技術。
單端匹配
在單端匹配中,將一定固定長度的短截線放置在距負載一定距離處。它僅用於固定頻率,因為對於任何頻率變化,都必須改變短截線的位置,而這通常不會進行。此方法不適用於同軸線。
雙端匹配
在雙端匹配中,兩個可變長度的短截線固定在某些位置。當負載變化時,只需調整短截線的長度即可實現匹配。這在實驗室實踐中被廣泛用作單頻匹配裝置。
下圖顯示了阻抗匹配的外觀。
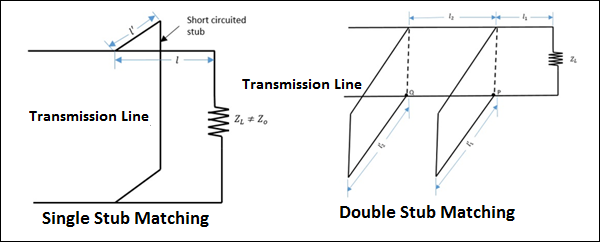
如上圖所示,在傳輸線中進行單端匹配和雙端匹配以實現阻抗匹配。