
微波工程 - 微波器件
與其他系統一樣,微波系統由許多微波元件構成,主要在一端具有電源,另一端具有負載,所有這些都透過波導、同軸電纜或傳輸線系統連線。
以下是波導的特性。
- 高信噪比
- 低衰減
- 較低的插入損耗
波導微波功能
考慮一個具有4個埠的波導。如果功率施加到一個埠,它會以一定的比例透過所有3個埠,其中一部分可能會從同一個埠反射回來。此概念在下圖中清楚地描繪。

散射引數
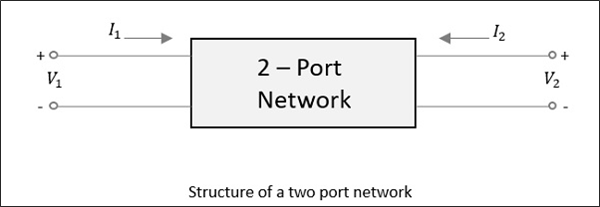
對於一個二埠網路,如下圖所示,如果功率施加在一個埠,正如我們剛才討論的那樣,大部分功率從另一個埠逸出,而一部分功率反射回同一個埠。在下圖中,如果施加V1或V2,則分別流過I1或I2電流。
如果電源施加到相對的埠,則需要考慮另外兩種組合。因此,對於一個二埠網路,可能出現2 × 2 = 4種組合。
當具有相關功率的行波透過埠散射時,微波結可以用S引數或散射引數來定義,這些引數以矩陣形式表示,稱為“散射矩陣”。
散射矩陣
它是一個方陣,給出了微波結各種輸入和輸出埠之間所有功率關係的組合。該矩陣的元素稱為“散射係數”或“散射(S)引數”。
考慮下圖。

這裡,電源透過第$i$條線連線,$a_1$是入射波,$b_1$是反射波。
如果給出一個$b_1$和$a_1$之間的關係,
$$b_1 = (反射係數)a_1 = S_{1i}a_1$$
其中
$S_{1i}$ = 第1條線的反射係數(其中$i$是輸入埠,$1$是輸出埠)
$1$ = 第1條線的反射
$i$ = 電源連線在第$i$條線上
如果阻抗匹配,則功率被傳輸到負載。如果負載阻抗與特性阻抗不匹配,則情況並非如此。然後,發生反射。這意味著如果
$$Z_l \neq Z_o$$
但是,如果這種不匹配存在於多個埠(例如'n'個埠),則i = 1到n(因為i可以是從1到n的任何線路)。
因此,我們有
$$b_1 = S_{11}a_1 + S_{12}a_2 + S_{13}a_3 + ............... + S_{1n}a_n$$
$$b_2 = S_{21}a_1 + S_{22}a_2 + S_{23}a_3 + ............... + S_{2n}a_n$$
$$.$$
$$.$$
$$.$$
$$.$$
$$.$$
$$b_n = S_{n1}a_1 + S_{n2}a_2 + S_{n3}a_3 + ............... + S_{nn}a_n$$
當整個內容以矩陣形式表示時,
$$\begin{bmatrix} b_1\\ b_2\\ b_3\\ .\\ .\\ .\\ b_n \end{bmatrix} = \begin{bmatrix} S_{11}& S_{12}& S_{13}& ...& S_{1n}\\ S_{21}& S_{22}& S_{23}& ...& S_{2n}\\ .& .& .& ...& . \\ .& .& .& ...& . \\ .& .& .& ...& . \\ S_{n1}& S_{n2}& S_{n3}& ...& S_{nn}\\ \end{bmatrix} \times \begin{bmatrix} a_1\\ a_2\\ a_3\\ .\\ .\\ .\\ a_n \end{bmatrix}$$
列矩陣 $[b]$ 散射矩陣 $[S]$矩陣 $[a]$
列矩陣$\left [ b \right ]$對應於反射波或輸出,而矩陣$\left [ a \right ]$對應於入射波或輸入。n×n階的散射列矩陣$\left [ s \right ]$包含反射係數和傳輸係數。因此,
$$\left [ b \right ] = \left [ S \right ]\left [ a \right ]$$
[S]矩陣的性質
散射矩陣表示為[S]矩陣。[S]矩陣有一些標準性質。它們是:
-
[S]始終是(nxn)階的方陣
[S]n×n
-
[S]是對稱矩陣
即,$S_{ij} = S_{ji}$
-
[S]是酉矩陣
即,$[S][S]^* = I$
任何一行或一列的每一項乘以另一行或一列的對應項的複共軛的乘積之和為零。即,
$$\sum_{i=j}^{n} S_{ik} S_{ik}^{*} = 0 \: for \: k \neq j$$
$$( k = 1,2,3, ... \: n ) \: and \: (j = 1,2,3, ... \: n)$$
-
如果某個第k個埠與結之間的電距離為$\beta _kI_k$,則涉及k的$S_{ij}$係數將乘以因子$e^{-j\beta kIk}$
在接下來的幾章中,我們將研究不同型別的微波三通。