微波工程 - 測量

---

---

在微波工程領域，存在許多應用，如第一章所述。因此，在使用不同的應用時，我們經常需要測量不同的值，例如功率、衰減、相移、駐波比、阻抗等，以便有效地使用。

在本章中，讓我們看看不同的測量技術。

功率測量

測量的微波功率是波導中任何位置的平均功率。功率測量可以分為三種類型。

• 低功率測量（0.01mW至10mW）

  示例 - 熱敏電阻技術

• 中功率測量（10mW至1W）

  示例 - 量熱計技術

• 高功率測量（>10W）

  示例 - 量熱計功率計

讓我們詳細瞭解一下。

低功率測量

約0.01mW至10mW範圍內的微波功率測量，可以理解為低功率測量。

熱敏電阻是一種用於低微波功率測量的器件。熱敏電阻中使用的元件可以是正溫度係數或負溫度係數。例如，燈絲具有正溫度係數，其電阻隨溫度升高而增大。熱敏電阻具有負溫度係數，其電阻隨溫度升高而減小。

任何一種都可以用在熱敏電阻中，但電阻的變化與用於測量的微波功率成正比。此熱敏電阻用作橋路中的一臂，以便任何產生的不平衡都會影響輸出。下圖顯示了一個使用熱敏電阻的典型橋路電路。

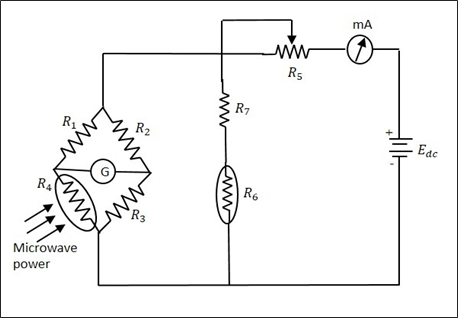
此處的毫安表給出流過電流的值。電池是可變的，透過改變它來獲得平衡，當熱敏電阻的行為導致不平衡時。在直流電池電壓中進行的這種調整與微波功率成正比。此電路的功率處理能力有限。

中功率測量

約10mW至1W範圍內的微波功率測量，可以理解為中功率測量。

採用特殊的負載，通常保持一定值的比熱容。待測功率施加到其輸入端，與負載原本保持的輸出溫度成比例地改變。溫度升高的差異指定了輸入到負載的微波功率。

此處使用橋路平衡技術來獲取輸出。熱傳遞方法用於功率測量，這是一種量熱技術。

高功率測量

約10W至50KW範圍內的微波功率測量，可以理解為高功率測量。

高微波功率通常由量熱計功率計測量，量熱計功率計可以是乾式或流通式。乾式之所以如此命名，是因為它使用同軸電纜，該電纜填充有具有高磁滯損耗的介電材料，而流通式之所以如此命名，是因為它使用水或油或某些液體，這些液體是微波的良好吸收劑。

液體進入負載前後溫度的變化用於校準值。這種方法的侷限性在於流量確定、校準和熱慣性等。

衰減測量

在實踐中，微波元件和器件通常會提供一些衰減。提供的衰減量可以透過兩種方式測量。它們是 - 功率比法和射頻替代法。

衰減是輸入功率與輸出功率之比，通常以分貝表示。

$$衰減（dB）= 10 \: log\frac{P_{in}}{P_{out}}$$

其中 $P_{in}$ = 輸入功率 和 $P_{out}$ = 輸出功率

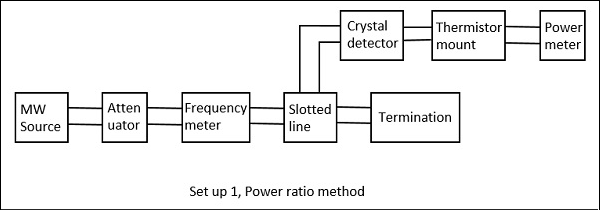
功率比法

在這種方法中，衰減測量分兩個步驟進行。

• 步驟1 - 在不使用需要計算衰減的器件的情況下，對整個微波工作臺的輸入和輸出功率進行測量。

• 步驟2 - 使用需要計算衰減的器件對整個微波工作臺的輸入和輸出功率進行測量。

比較這些功率的比率，即可得到衰減值。

下圖是解釋此方法的兩個設定。

缺點 - 當輸入功率低且網路的衰減較大時，功率和衰減測量可能不準確。

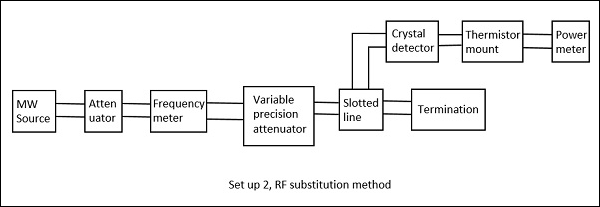
射頻替代法

在這種方法中，衰減測量分三個步驟進行。

• 步驟1 - 測量整個微波工作臺在需要計算衰減的網路下的輸出功率。

• 步驟2 - 透過用精密校準的衰減器替換網路來測量整個微波工作臺的輸出功率。

• 步驟3 - 現在，調整此衰減器以獲得與使用網路時測量的相同功率。

下圖是解釋此方法的兩個設定。

衰減器上調整的值直接給出網路的衰減。這裡避免了上述方法中的缺點，因此這是測量衰減的更好方法。

相移測量

在實際工作條件下，訊號可能會發生相對於實際訊號的相位變化。為了測量這種相移，我們使用比較技術，透過該技術我們可以校準相移。

計算相移的設定如下圖所示。

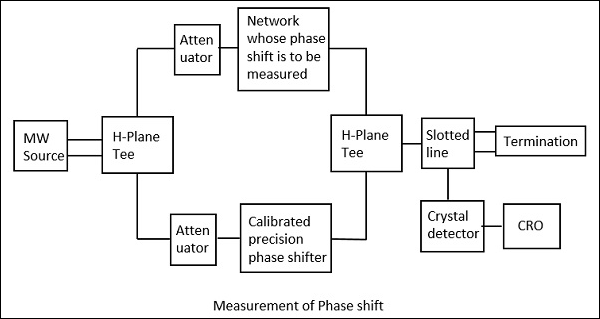
這裡，在微波源產生訊號後，它透過一個H面T型接頭，其中一個埠連線到需要測量相移的網路，另一個埠連線到一個可調節的精密相移器。

解調後的輸出是一個1KHz正弦波，在連線的示波器上觀察到。調整此相移器，使其1KHz正弦波輸出也與上述輸出匹配。透過在雙模式示波器上觀察來完成匹配後，此精密相移器會給我們相移讀數。下圖清楚地說明了這一點。

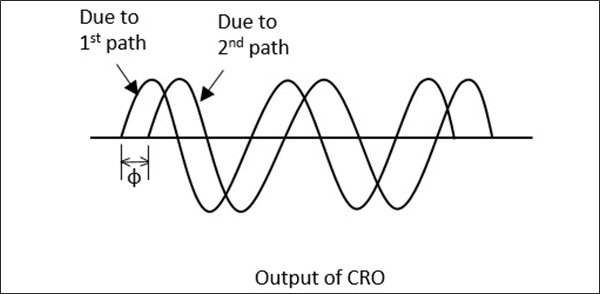
此過程是相移測量中最常用的方法。現在，讓我們看看如何計算駐波比。

駐波比測量

在任何微波實際應用中，任何型別的阻抗失配都會導致駐波的形成。這些駐波的強度由電壓駐波比（$VSWR$）測量。最大電壓與最小電壓之比給出$VSWR$，表示為$S$。

$$S = \frac{V_{max}}{V_{min}} = \frac{1+\rho }{1-\rho}$$

其中，$\rho = 反射係數 = \frac{P_{反射}}{P_{入射}}$

$VSWR$的測量可以透過兩種方式進行，低$VSWR$和高$VSWR$測量。

低駐波比測量（S <10）

低$VSWR$的測量可以透過調整衰減器來獲得駐波比計（即直流毫伏表）上的讀數。可以透過調整槽線和衰減器的方式獲取讀數，使直流毫伏表顯示滿量程讀數以及最小讀數。

現在，計算這兩個讀數以確定網路的$VSWR$。

高駐波比測量（S>10）

大於10的高$VSWR$的測量可以透過一種稱為雙最小值法的方法進行測量。在這種方法中，獲取最小值的讀數，以及最小值前半波峰和後半波峰中最小值一半處的讀數。下圖可以幫助理解。

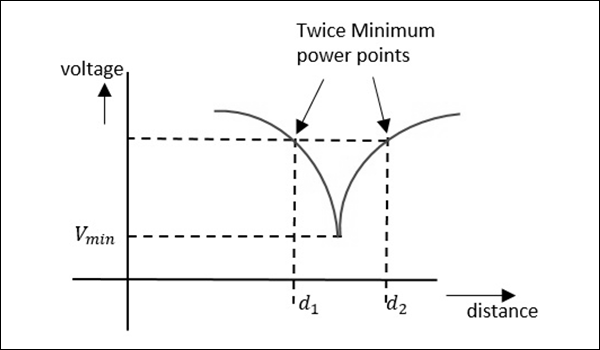
現在，可以透過以下關係計算$VSWR$：

$$VSWR = \frac{\lambda_{g}}{\pi(d_2-d_1)}$$

其中，$\lambda_g$ 是導波波長

$$\lambda_g = \frac{\lambda_0}{\sqrt{1-(\frac{\lambda_0}{\lambda_c})^2}} \quad 其中 \: \lambda_0 \: = {c}/{f}$$

由於這裡考慮了兩個最小點，因此稱為雙最小值法。現在，讓我們學習一下阻抗測量。

阻抗測量

除了魔T之外，我們還有兩種不同的方法，一種是使用槽線，另一種是使用反射計。

使用槽線測量阻抗

在這種方法中，使用槽線和負載$Z_L$測量阻抗，並使用此方法確定$V_{max}$和$V_{min}$。在這種方法中，阻抗測量分兩個步驟進行。

• 步驟1 - 使用負載$Z_L$確定Vmin。

• 步驟2 - 透過短路負載來確定Vmin。

如下圖所示。

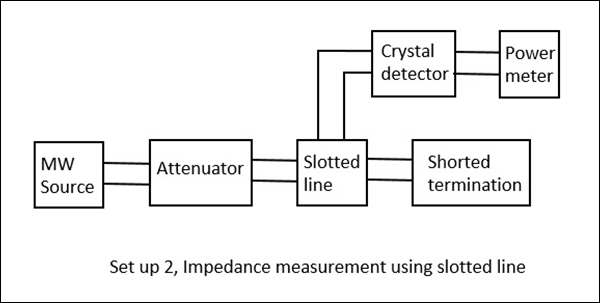
當我們嘗試使用負載獲取$V_{max}$和$V_{min}$的值時，我們會得到某些值。但是，如果透過短路負載執行相同的操作，則最小值會向左或向右移動。如果此偏移向左，則表示負載具有感性；如果此偏移向右，則表示負載具有容性。下圖解釋了這一點。

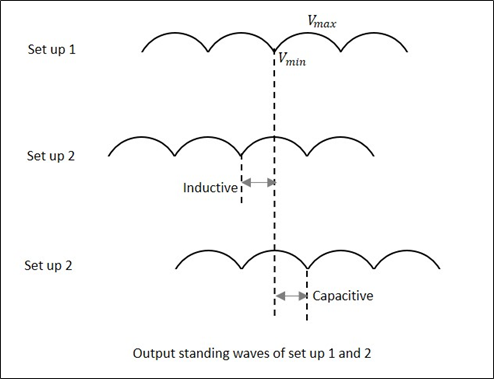
透過記錄資料，計算未知阻抗。可以獲得阻抗和反射係數$\rho$的幅度和相位。

使用反射計測量阻抗

與槽線不同，反射計只能找到阻抗的幅度，而不能找到相位角。在這種方法中，採用兩個方向相同但方向不同的定向耦合器。

這兩個耦合器用於從負載中取樣入射功率$P_i$和反射功率$P_r$。反射計的連線方式如下圖所示。它用於獲取反射係數$\rho$的幅度，從中可以得到阻抗。

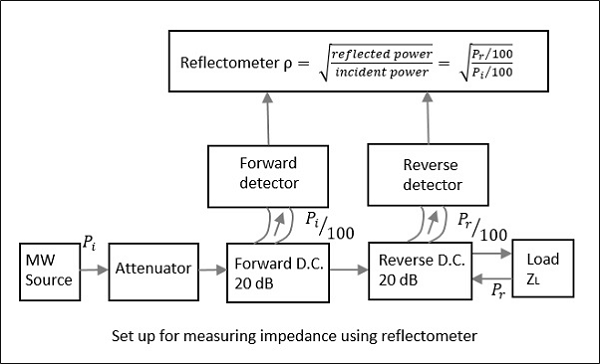
從反射計讀數中，我們有

$$\rho = \sqrt{\frac{P_r}{P_i}}$$

根據$\rho$的值，可以計算$VSWR$，即$S$和阻抗，公式如下：

$$S = \frac{1+\rho}{1-\rho} \quad 和 \quad \frac{z-z_g}{z+z_g} = \rho$$

其中，$z_g$ 是已知波阻抗，$z$ 是未知阻抗。

雖然這裡觀察了正向和反向波引數，但由於耦合器的方向特性，不會出現干擾。衰減器有助於維持低輸入功率。

諧振腔品質因數Q的測量

雖然測量諧振腔Q值的方法有三種，例如傳輸法、阻抗法和瞬態衰減或減量法，但最簡單、最常用的方法是傳輸法。因此，讓我們看一下它的測量設定。

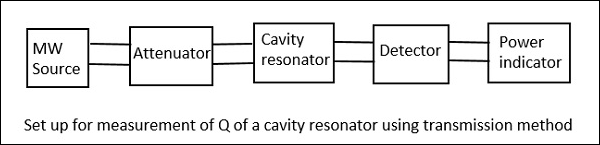
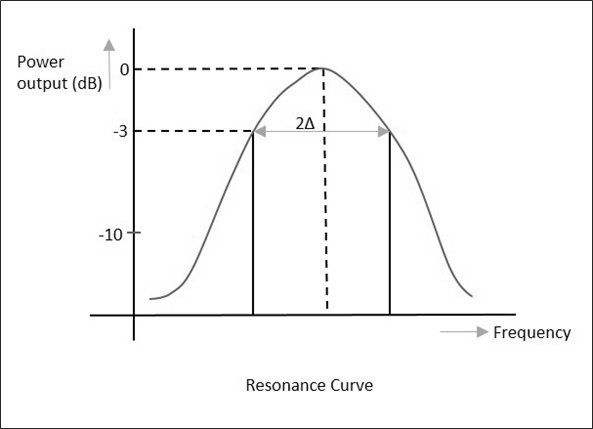
在這種方法中，諧振腔充當傳輸裝置。輸出訊號作為頻率的函式繪製，從而產生如以下圖所示的諧振曲線。

從上面的設定中，微波源的訊號頻率發生變化，保持訊號電平恆定，然後測量輸出功率。諧振腔調諧到此頻率，並再次記下訊號電平和輸出功率以觀察差異。

當繪製輸出時，會獲得諧振曲線，從中我們可以注意到半功率頻寬（HPBW）$(2 \Delta)$值。

$$2\Delta = \pm \frac{1}{Q_L}$$

其中，$Q_L$是負載值

$$或 \quad Q_L = \pm \frac{1}{2\Delta} = \pm \frac{w}{2(w-w_0)}$$

如果忽略微波源和腔體之間的耦合以及探測器和腔體之間的耦合，則

$$Q_L = Q_0 \: (無負載Q)$$

缺點

該系統的主要缺點是，由於工作頻寬窄，在非常高的Q值系統中精度較差。

我們已經介紹了許多不同引數的多種測量技術。現在，讓我們嘗試解決一些關於這些技術的示例問題。