正弦波振盪器

---

---

振盪器是一種產生週期性訊號的電子電路。如果振盪器產生正弦波振盪，則稱為正弦波振盪器。它將來自直流電源的輸入能量轉換為具有周期性訊號的交流輸出能量。此週期性訊號將具有特定的頻率和幅度。

正弦波振盪器的框圖如下所示：

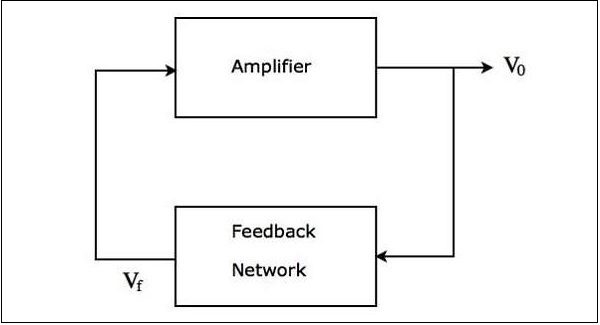
上圖主要由兩個模組組成：放大器和反饋網路。反饋網路將放大器輸出的一部分作為輸入，併產生電壓訊號。此電壓訊號用作放大器的輸入。

當滿足以下兩個條件時，上圖所示的正弦波振盪器框圖產生正弦波振盪：

• 上述正弦波振盪器框圖的環路增益$A_{v}\beta$必須大於或等於1。這裡，$A_{v}$和$\beta$分別為放大器的增益和反饋網路的增益。

• 上述正弦波振盪器框圖環路的總相移必須為0⁰或360⁰。

上述兩個條件合稱為巴克豪森判據。

基於運放的振盪器

有兩種型別的基於運放的振盪器。

• RC移相振盪器
• 維恩電橋振盪器

本節將詳細討論每個振盪器。

RC移相振盪器

基於運放的振盪器，它藉助反相放大器和反饋網路在輸出端產生正弦電壓訊號，被稱為RC移相振盪器。此反饋網路由三個級聯的RC網路組成。

RC移相振盪器的電路圖如下所示：

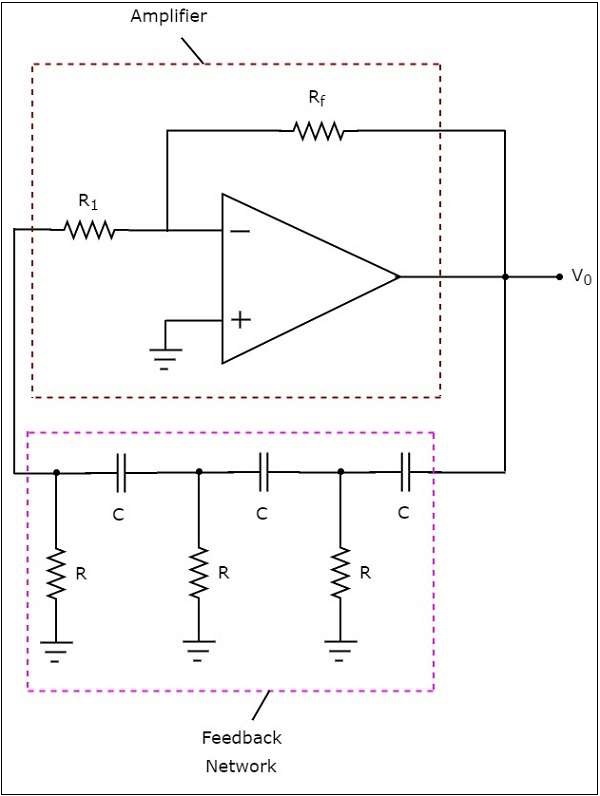
在上圖電路中，運放工作在反相模式。因此，它提供180⁰的相移。上述電路中存在的反饋網路也提供180⁰的相移，因為每個RC網路提供60⁰的相移。因此，上述電路在某個頻率下提供360⁰的總相移。

• RC移相振盪器的輸出頻率為：

$$f=\frac{1}{2\Pi RC\sqrt[]{6}}$$

• 反相放大器的增益$A_{v}$應大於或等於-29，

$$即，-\frac{R_f}{R_1}\geq-29$$

$$=>\frac{R_f}{R_1}\geq-29$$

$$=>R_{f}\geq29R_{1}$$

因此，為了在RC移相振盪器的輸出端產生持續振盪，我們應將反饋電阻$R_{f}$的值至少考慮為電阻$R_{1}$值的29倍。

維恩電橋振盪器

基於運放的振盪器，它藉助同相放大器和反饋網路在輸出端產生正弦電壓訊號，被稱為維恩電橋振盪器。

維恩電橋振盪器的電路圖如下所示：

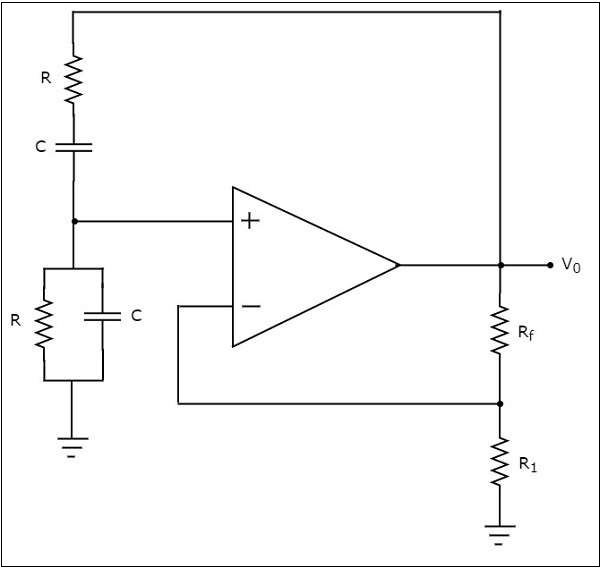
在上述維恩電橋振盪器電路中，運放工作在同相模式。因此，它提供00的相移。所以，上述電路中存在的反饋網路不應提供任何相移。

如果反饋網路提供了一些相移，則我們必須平衡電橋，以使不存在任何相移。因此，上述電路在某個頻率下提供0⁰的總相移。

• 維恩電橋振盪器的輸出頻率為

$$f=\frac{1}{2\Pi RC}$$

• 同相放大器的增益$A_{v}$應大於或等於3

$$即，1+\frac{R_f}{R_1}\geq3$$

$$=>\frac{R_f}{R_1}\geq2$$

$$=>R_{f}\geq2R_{1}$$

因此，為了在維恩電橋振盪器的輸出端產生持續振盪，我們應將反饋電阻$R_{f}$的值至少考慮為電阻$R_{1}$值的2倍。