
微分器和積分器
執行微分和積分等數學運算的電子電路分別稱為微分器和積分器。
本章詳細討論了基於運放的微分器和積分器。請注意,這些也屬於運放的線性應用。
微分器
微分器是一種電子電路,其輸出等於其輸入的一階導數。本節詳細討論了基於運放的微分器。
基於運放的微分器產生一個輸出,該輸出等於施加到其反相輸入端的輸入電壓的微分。基於運放的微分器的電路圖如下所示:
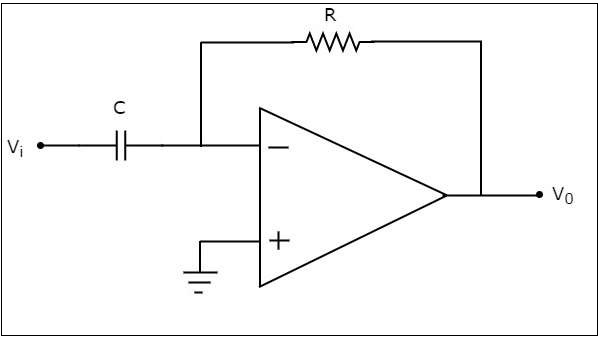
在上圖電路中,運放的反相輸入端連線到地。這意味著零伏特施加到其反相輸入端。
根據虛短概念,運放反相輸入端的電壓將等於其同相輸入端的電壓。因此,運放反相輸入端的電壓將為零伏特。
反相輸入端節點的節點方程為:
$$C\frac{\text{d}(0-V_{i})}{\text{d}t}+\frac{0-V_0}{R}=0$$
$$=>-C\frac{\text{d}V_{i}}{\text{d}t}=\frac{V_0}{R}$$
$$=>V_{0}=-RC\frac{\text{d}V_{i}}{\text{d}t}$$
如果$RC=1\sec$,則輸出電壓$V_{0}$將為:
$$V_{0}=-\frac{\text{d}V_{i}}{\text{d}t}$$
因此,上面所示的基於運放的微分器電路將產生一個輸出,該輸出是輸入電壓$V_{i}$的微分,當電阻和電容的阻抗大小互為倒數時。
請注意,輸出電壓$V_{0}$帶有負號,這表示輸入和輸出之間存在1800的相位差。
積分器
積分器是一種電子電路,其輸出是施加輸入的積分。本節討論了基於運放的積分器。
基於運放的積分器產生一個輸出,該輸出是施加到其反相輸入端的輸入電壓的積分。基於運放的積分器的電路圖如下所示:

在上圖所示的電路中,運放的同相輸入端連線到地。這意味著零伏特施加到其同相輸入端。
根據虛短概念,運放反相輸入端的電壓將等於其同相輸入端的電壓。因此,運放反相輸入端的電壓將為零伏特。
反相輸入端的節點方程為:
$$\frac{0-V_i}{R}+C\frac{\text{d}(0-V_{0})}{\text{d}t}=0$$
$$=>\frac{-V_i}{R}=C\frac{\text{d}V_{0}}{\text{d}t}$$
$$=>\frac{\text{d}V_{0}}{\text{d}t}=-\frac{V_i}{RC}$$
$$=>{d}V_{0}=\left(-\frac{V_i}{RC}\right){\text{d}t}$$
對上述方程兩邊積分,得到:
$$\int{d}V_{0}=\int\left(-\frac{V_i}{RC}\right){\text{d}t}$$
$$=>V_{0}=-\frac{1}{RC}\int V_{t}{\text{d}t}$$
如果$RC=1\sec$,則輸出電壓$V_{0}$將為:
$$V_{0}=-\int V_{i}{\text{d}t}$$
因此,上面討論的基於運放的積分器電路將產生一個輸出,該輸出是輸入電壓$V_{i}$的積分,當電阻和電容的阻抗大小互為倒數時。
注意 - 輸出電壓$V_{0}$帶有負號,這表示輸入和輸出之間存在1800的相位差。