積體電路基礎

一個電子電路是由多個電子元件連線在一起，用於實現特定功能的。

簡單的電子電路設計起來比較容易，因為它只需要很少的離散電子元件和連線。但是，設計複雜的電子電路則比較困難，因為它需要大量的離散電子元件及其連線。構建此類複雜電路也需要花費時間，並且可靠性也較低。這些困難可以透過積體電路來克服。

積體電路 (IC)

如果將多個電子元件互連在一個半導體材料晶片上，則該晶片稱為積體電路 (IC)。它包含有源和無源元件。

本章將討論IC的優點和型別。

積體電路的優點

積體電路提供了許多優點。下面將詳細介紹：

體積小巧 - 對於給定的功能，與使用分立電路構建的電路相比，使用IC可以獲得更小的電路尺寸。
重量輕 - 與用於實現相同IC功能的分立電路的重量相比，使用IC構建的電路重量更輕。使用IC，與使用分立電路構建的電路相比。
功耗低 - 由於其尺寸小巧和構造，IC的功耗低於傳統電路。
成本降低 - 由於其製造技術和使用的材料少於分立電路，因此IC的成本大大降低。
可靠性提高 - 由於它們使用的連線更少，因此與數位電路相比，IC的可靠性更高。
工作速度提高 - 由於其開關速度和功耗降低，IC的工作速度更快。

積體電路的型別

積體電路主要分為兩種- 模擬積體電路和數字積體電路。

模擬積體電路

在訊號幅度的整個連續值範圍內工作的積體電路稱為模擬積體電路。它們進一步分為以下兩種型別：

線性積體電路 - 如果模擬IC的電壓和電流之間存線上性關係，則稱其為線性IC。IC 741，一個8引腳雙列直插式封裝(DIP)運放，就是一個線性IC的例子。
射頻積體電路 - 如果模擬IC的電壓和電流之間存在非線性關係，則稱其為非線性IC。非線性IC也稱為射頻IC。

數字積體電路

如果積體電路僅在幾個預定義的電平上工作，而不是在訊號幅度的整個連續值範圍內工作，則稱為數字積體電路。

在接下來的章節中，我們將討論各種線性積體電路及其應用。

運算放大器基礎

運算放大器，也稱為運放，是一種積體電路，可用於執行各種線性、非線性以及數學運算。運放是一種直耦高增益放大器。您可以使用交流和直流訊號來操作運放。本章將討論運放的特性和型別。

運算放大器的構造

運放由差分放大器、電平轉換器和輸出級組成。差分放大器位於運放的輸入級，因此運放具有兩個輸入端。其中一個端子稱為反相輸入端，另一個稱為同相輸入端。端子的命名是基於其各自輸入和輸出之間的相位關係。

運算放大器的特性

運算放大器的重要特性或引數如下：

開環電壓增益
輸出失調電壓
共模抑制比
壓擺率

本節將詳細討論這些特性，如下所示：

開環電壓增益

運放的開環電壓增益是指在沒有反饋路徑的情況下其差分增益。

在數學上，運放的開環電壓增益表示為：

$$A_{v}= \frac{v_0}{v_1-v_2}$$

輸出失調電壓

當運放的差分輸入電壓為零時，其輸出端存在的電壓稱為輸出失調電壓。

共模抑制比

運放的共模抑制比 (CMRR) 定義為閉環差分增益 $A_{d}$ 和共模增益 $A_{c}$ 的比值。

在數學上，CMRR可以表示為：

$$CMRR=\frac{A_{d}}{A_{c}}$$

請注意，運放的共模增益 $A_{c}$ 是共模輸出電壓與共模輸入電壓之比。

壓擺率

運放的壓擺率定義為由於階躍輸入電壓導致的輸出電壓變化的最大速率。

在數學上，壓擺率 (SR) 可以表示為：

$$SR=Maximum\:of\:\frac{\text{d}V_{0}}{\text{d}t}$$

其中，$V_{0}$ 是輸出電壓。通常，壓擺率以 $V/\mu\:Sec$ 或 $V/m\:Sec$ 為單位測量。

運算放大器的型別

運放用一個帶有兩個輸入和一個輸出的三角形符號表示。

運放主要分為兩種：理想運放和實際運放。

下面將詳細介紹：

理想運放

理想運放只存在於理論中，實際上並不存在。理想運放的等效電路如下圖所示：

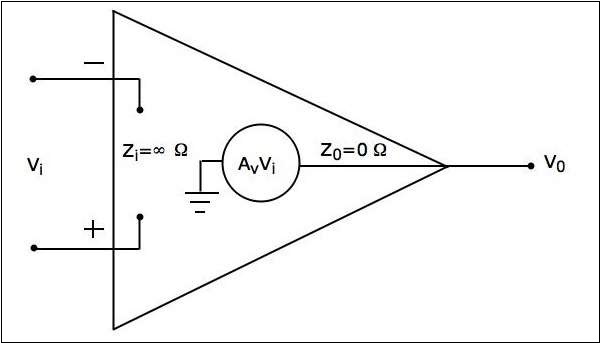
理想運放具有以下特性：

輸入阻抗 $Z_{i}=\infty\Omega$
輸出阻抗 $Z_{0}=0\Omega$
開環電壓增益 $A_{v}=\infty$
如果（差分）輸入電壓 $V_{i}=0V$，則輸出電壓將為 $V_{0}=0V$
頻寬為無窮大。這意味著，理想運放將放大任何頻率的訊號，而不會有任何衰減。
共模抑制比(CMRR)為無窮大。
壓擺率(SR)為無窮大。這意味著，理想運放將立即響應輸入階躍電壓，從而產生輸出變化。

實際運放

實際上，運放並非理想的，由於製造過程中的某些缺陷，它們會偏離其理想特性。實際運放的等效電路如下圖所示：

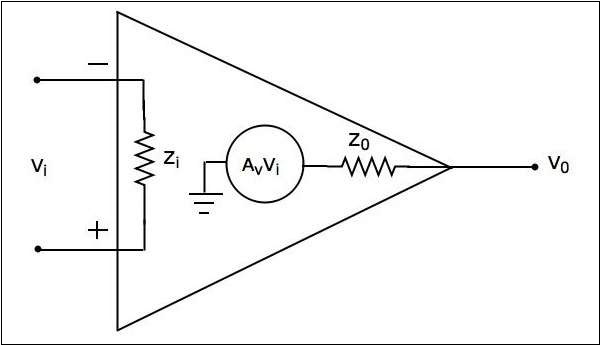
實際運放具有以下特性：

輸入阻抗 $Z_{i}$ 約為兆歐姆級。
輸出阻抗 $Z_{0}$ 約為幾歐姆級。
開環電壓增益 $A_{v}$ 將很高。

選擇實際運放時，應檢查其是否滿足以下條件：

輸入阻抗 $Z_{i}$ 應儘可能高。
輸出阻抗 $Z_{0}$ 應儘可能低。
開環電壓增益 $A_{v}$ 應儘可能高。
輸出失調電壓應儘可能低。
工作頻寬應儘可能寬。
CMRR應儘可能高。
壓擺率應儘可能高。

注意 - IC 741運放是最流行和最實用的運放。

運放應用

如果電路的輸入和輸出之間存線上性關係，則稱該電路為線性電路。類似地，如果電路的輸入和輸出之間存在非線性關係，則稱該電路為非線性電路。

運放可用於線性應用和非線性應用。以下是運放的基本應用：

反相放大器
同相放大器
電壓跟隨器

本章將詳細討論這些基本應用。

反相放大器

反相放大器透過電阻 $R_{1}$ 將輸入引入其反相輸入端，並將其放大後的版本作為輸出產生。該放大器不僅放大輸入，還對其進行反相（改變其符號）。

反相放大器的電路圖如下所示：

請注意，對於運放，反相輸入端的電壓等於其同相輸入端的電壓。在物理上，這兩個端子之間沒有短路，但在虛擬上，它們是短路的。

在上圖所示的電路中，同相輸入端連線到地。這意味著在運放的同相輸入端施加了零伏電壓。

根據虛短概念，運放的反相輸入端的電壓將為零伏。

該端子節點處的節點方程如下所示：

$$\frac{0-V_i}{R_1}+ \frac{0-V_0}{R_f}=0$$

$$=>\frac{-V_i}{R_1}= \frac{V_0}{R_f}$$

$$=>V_{0}=\left(\frac{-R_f}{R_1}\right)V_{t}$$

$$=>\frac{V_0}{V_i}= \frac{-R_f}{R_1}$$

輸出電壓 $V_{0}$ 和輸入電壓 $V_{i}$ 之比是電壓增益或放大器的增益。因此，反相放大器的增益等於 $-\frac{R_f}{R_1}$。

請注意，反相放大器的增益帶有負號。這表示輸入和輸出之間存在 180⁰ 的相位差。

同相放大器

非反相放大器將輸入訊號透過其非反相端輸入，並在輸出端產生放大後的版本。顧名思義，這種放大器只是放大輸入訊號，而不會反相或改變輸出訊號的符號。

非反相放大器的電路圖如下所示：

在上圖電路中，輸入電壓 $V_{i}$ 直接施加到運放的非反相輸入端。因此，運放非反相輸入端的電壓將為 $V_{i}$。

利用分壓原理，我們可以計算運放反相輸入端的電壓，如下所示：

$$=>V_{1} = V_{0}\left(\frac{R_1}{R_1+R_f}\right)$$

根據虛短路概念，運放的反相輸入端電壓與非反相輸入端電壓相同。

$$=>V_{1} = V_{i}$$

$$=>V_{0}\left(\frac{R_1}{R_1+R_f}\right)=V_{i}$$

$$=>\frac{V_0}{V_i}=\frac{R_1+R_f}{R_1}$$

$$=>\frac{V_0}{V_i}=1+\frac{R_f}{R_1}$$

現在，輸出電壓 $V_{0}$ 與輸入電壓 $V_{i}$ 的比值，即電壓增益或非反相放大器的增益，等於 $1+\frac{R_f}{R_1}$。

請注意，非反相放大器的增益具有正號。這表明輸入和輸出之間沒有相位差。

電壓跟隨器

電壓跟隨器是一種電子電路，其輸出跟隨輸入電壓。它是非反相放大器的一種特殊情況。

如果我們將反饋電阻 $R_{f}$ 的值視為零歐姆，或將電阻 $R_1$ 的值視為無窮大，則非反相放大器將變成電壓跟隨器。電壓跟隨器的電路圖如下所示：

在上圖電路中，輸入電壓 $V_{i}$ 直接施加到運放的非反相輸入端。因此，運放非反相輸入端的電壓等於 $V_{i}$。這裡，輸出端直接連線到運放的反相輸入端。因此，運放反相輸入端的電壓等於 $V_{0}$。

根據虛短路概念，運放的反相輸入端電壓與非反相輸入端電壓相同。

$$=>V_{0} = V_{i}$$

因此，電壓跟隨器的輸出電壓 $V_{0}$ 等於其輸入電壓 $V_{i}$。

因此，電壓跟隨器的增益等於1，因為電壓跟隨器的輸出電壓 $V_{0}$ 和輸入電壓 $V_{i}$ 相同。

算術電路

在上一章中，我們討論了運放的基本應用。請注意，它們屬於運放的線性運算。在本章中，讓我們討論算術電路，它們也是運放的線性應用。

執行算術運算的電子電路稱為算術電路。使用運放，您可以構建基本的算術電路，例如加法器和減法器。在本章中，您將詳細瞭解它們。

加法器

加法器是一種電子電路，其輸出等於施加的輸入之和。本節討論基於運放的加法器電路。

基於運放的加法器產生一個輸出，該輸出等於施加到其反相輸入端的輸入電壓之和。由於輸出是放大的，因此它也稱為加法放大器。

基於運放的加法器的電路圖如下所示：

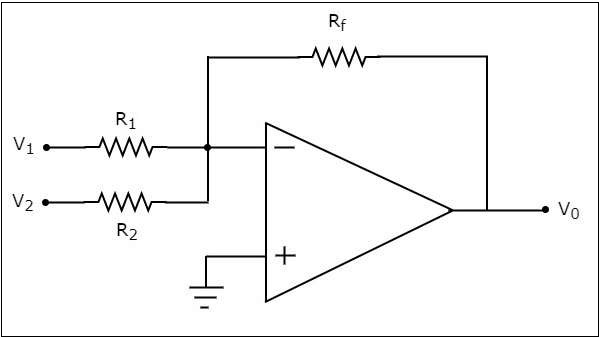
在上圖電路中，運放的非反相輸入端連線到地。這意味著在非反相輸入端施加了零伏電壓。

根據虛短路概念，運放的反相輸入端電壓與非反相輸入端電壓相同。因此，運放反相輸入端的電壓將為零伏。

反相輸入端節點的節點方程為

$$\frac{0-V_1}{R_1}+\frac{0-V_2}{R_2}+\frac{0-V_0}{R_f}=0$$

$$=>\frac{V_1}{R_1}-\frac{V_2}{R_2}=\frac{V_0}{R_f}$$

$$=>V_{0}=R_{f}\left(\frac{V_1}{R_1}+\frac{V_2}{R_2}\right)$$

如果 $R_{f}=R_{1}=R_{2}=R$，則輸出電壓 $V_{0}$ 將為：

$$V_{0}=-R{}\left(\frac{V_1}{R}+\frac{V_2}{R}\right)$$

$$=>V_{0}=-(V_{1}+V_{2})$$

因此，上面討論的基於運放的加法器電路將產生兩個輸入電壓 $v_{1}$ 和 $v_{1}$ 的和作為輸出，前提是電路中所有電阻的值都相同。請注意，加法器電路的輸出電壓 $V_{0}$ 具有負號，這表明輸入和輸出之間存在 180⁰ 的相位差。

減法器

減法器是一種電子電路，其輸出等於施加的輸入之差。本節討論基於運放的減法器電路。

基於運放的減法器產生一個輸出，該輸出等於施加到其反相和非反相輸入端的輸入電壓之差。由於輸出是放大的，因此它也稱為差分放大器。

基於運放的減法器的電路圖如下所示：

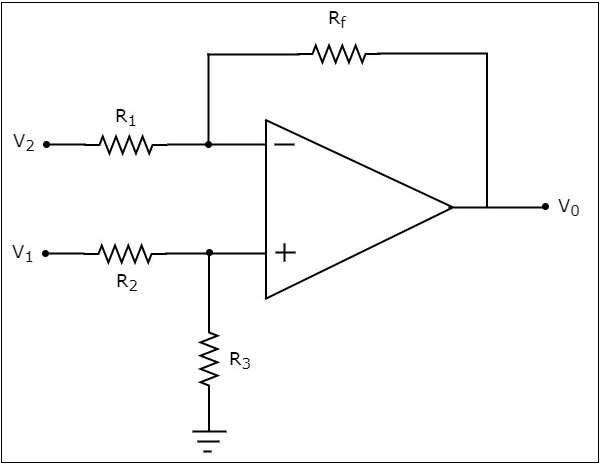
現在，讓我們使用以下步驟，利用疊加定理找到上述電路的輸出電壓 $V_{0}$ 的表示式：

步驟 1

首先，讓我們透過僅考慮 $V_{1}$ 來計算輸出電壓 $V_{01}$。

為此，透過將其短路來消除 $V_{2}$。然後，我們得到修改後的電路圖，如下所示：

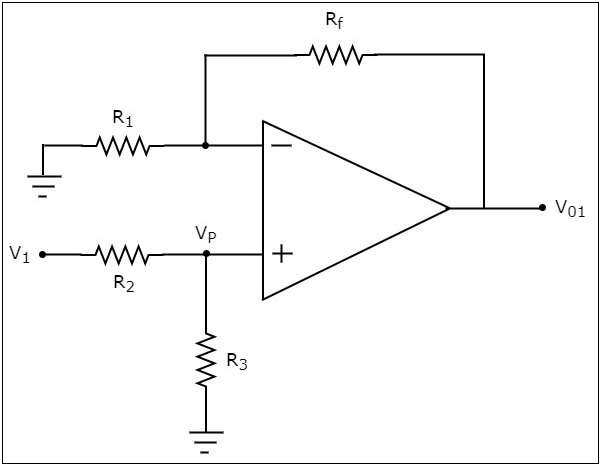
現在，使用分壓原理計算運放非反相輸入端的電壓。

$$=>V_{p}=V_{1}\left(\frac{R_3}{R_2+R_3}\right)$$

現在，上述電路看起來像一個具有輸入電壓 $V_{p}$ 的非反相放大器。因此，上述電路的輸出電壓 $V_{01}$ 將為

$$V_{01}=V_{p}\left(1+\frac{R_f}{R_1}\right)$$

將 $V_{p}$ 的值代入上述方程，我們得到僅考慮 $V_{1}$ 時得到的輸出電壓 $V_{01}$，如下所示：

$$V_{01}=V_{1}\left(\frac{R_3}{R_2+R_3}\right)\left(1+\frac{R_f}{R_1}\right)$$

步驟 2

在此步驟中，讓我們透過僅考慮 $V_{2}$ 來找到輸出電壓 $V_{02}$。與上述步驟類似，透過將其短路來消除 $V_{1}$。修改後的電路圖如下所示。

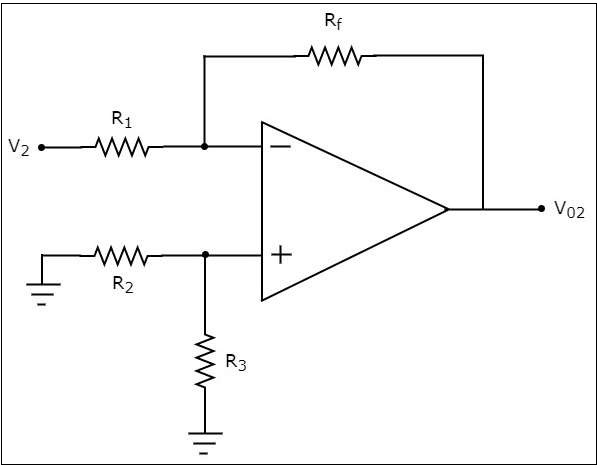
您可以觀察到，運放非反相輸入端的電壓將為零伏。這意味著，上述電路只是一個反相運放。因此，上述電路的輸出電壓 $V_{02}$ 將為：

$$V_{02}=\left(-\frac{R_f}{R_1}\right)V_{2}$$

步驟 3

在此步驟中，我們將透過將步驟 1 和步驟 2 中獲得的輸出電壓相加來獲得減法器電路的輸出電壓 $V_{0}$。在數學上，它可以寫成

$$V_{0}=V_{01}+V_{02}$$

將 $V_{01}$ 和 $V_{02}$ 的值代入上述方程，我們得到：

$$V_{0}=V_{1}\left(\frac{R_3}{R_2+R_3}\right)\left(1+\frac{R_f}{R_1}\right)+\left(-\frac{R_f}{R_1}\right)V_{2}$$

$$=>V_{0}=V_{1}\left(\frac{R_3}{R_2+R_3}\right)\left(1+\frac{R_f}{R_1}\right)-\left(\frac{R_f}{R_1}\right)V_{2}$$

如果 $R_{f}=R_{1}=R_{2}=R_{3}=R$，則輸出電壓 $V_{0}$ 將為

$$V_{0}=V_{1}\left(\frac{R}{R+R}\right)\left(1+\frac{R}{R}\right)-\left(\frac{R}{R}\right)V_{2}$$

$$=>V_{0}=V_{1}\left(\frac{R}{2R}\right)(2)-(1)V_{2}$$

$$V_{0}=V_{1}-V_{2}$$

因此，上面討論的基於運放的減法器電路將產生一個輸出，該輸出是兩個輸入電壓 $V_{1}$ 和 $V_{2}$ 的差，前提是電路中所有電阻的值都相同。

微分器和積分器

執行數學運算（如微分和積分）的電子電路分別稱為微分器和積分器。

本章詳細討論了基於運放的微分器和積分器。請注意，這些也屬於運放的線性應用。

微分器

微分器是一種電子電路，其輸出等於其輸入的一階導數。本節詳細討論了基於運放的微分器。

基於運放的微分器產生一個輸出，該輸出等於施加到其反相輸入端的輸入電壓的微分。基於運放的微分器的電路圖如下所示：

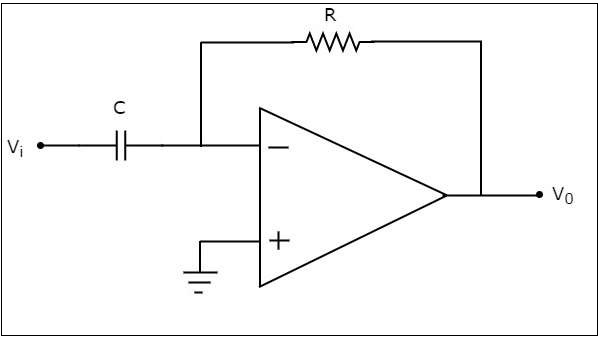
在上圖電路中，運放的非反相輸入端連線到地。這意味著在非反相輸入端施加了零伏電壓。

根據虛短路概念，運放反相輸入端的電壓將等於其非反相輸入端存在的電壓。因此，運放反相輸入端的電壓將為零伏。

反相輸入端節點的節點方程為：

$$C\frac{\text{d}(0-V_{i})}{\text{d}t}+\frac{0-V_0}{R}=0$$

$$=>-C\frac{\text{d}V_{i}}{\text{d}t}=\frac{V_0}{R}$$

$$=>V_{0}=-RC\frac{\text{d}V_{i}}{\text{d}t}$$

如果 $RC=1\sec$，則輸出電壓 $V_{0}$ 將為：

$$V_{0}=-\frac{\text{d}V_{i}}{\text{d}t}$$

因此，上面所示的基於運放的微分器電路將產生一個輸出，該輸出是輸入電壓 $V_{i}$ 的微分，前提是電阻和電容的阻抗大小互為倒數。

請注意，輸出電壓 $V_{0}$ 具有負號，這表明輸入和輸出之間存在 180⁰ 的相位差。

積分器

積分器是一種電子電路，其輸出是施加輸入的積分。本節討論基於運放的積分器。

基於運放的積分器產生一個輸出，該輸出是施加到其反相輸入端的輸入電壓的積分。基於運放的積分器的電路圖如下所示：

在上圖所示的電路中，運放的非反相輸入端連線到地。這意味著在非反相輸入端施加了零伏電壓。

根據虛短路概念，運放反相輸入端的電壓將等於其非反相輸入端存在的電壓。因此，運放反相輸入端的電壓將為零伏。

反相輸入端的節點方程為：

$$\frac{0-V_i}{R}+C\frac{\text{d}(0-V_{0})}{\text{d}t}=0$$

$$=>\frac{-V_i}{R}=C\frac{\text{d}V_{0}}{\text{d}t}$$

$$=>\frac{\text{d}V_{0}}{\text{d}t}=-\frac{V_i}{RC}$$

$$=>{d}V_{0}=\left(-\frac{V_i}{RC}\right){\text{d}t}$$

對上述方程的兩邊進行積分，我們得到：

$$\int{d}V_{0}=\int\left(-\frac{V_i}{RC}\right){\text{d}t}$$

$$=>V_{0}=-\frac{1}{RC}\int V_{t}{\text{d}t}$$

如果 $RC=1\sec$，則輸出電壓 $V_{0}$ 將為：

$$V_{0}=-\int V_{i}{\text{d}t}$$

因此，上面討論的基於運放的積分器電路將產生一個輸出，該輸出是輸入電壓 $V_{i}$ 的積分，前提是電阻和電容的阻抗大小互為倒數。

注意 - 輸出電壓 $V_{0}$ 帶有負號，這表明輸入和輸出之間存在 180⁰ 的相位差。

電量轉換器

電壓和電流是基本的電學量。根據需要，它們可以相互轉換。電壓到電流轉換器和電流到電壓轉換器是兩種有助於這種轉換的電路。這些也是運放的線性應用。本章將詳細討論它們。

電壓到電流轉換器

電壓到電流轉換器或V到I轉換器是一種電子電路，它以電流作為輸入，併產生電壓作為輸出。本節討論基於運放的電壓到電流轉換器。

基於運放的電壓到電流轉換器在電壓施加到其同相端時產生輸出電流。基於運放的電壓到電流轉換器的電路圖如下所示。

在上圖所示的電路中，輸入電壓 $V_{i}$ 施加到運放的同相輸入端。根據虛短概念，運放的反相輸入端的電壓將等於其同相輸入端的電壓。因此，運放的反相輸入端的電壓將為 $V_{i}$。

反相輸入端節點的節點方程為：

$$\frac{V_i}{R_1}-I_{0}=0$$

$$=>I_{0}=\frac{V_t}{R_1}$$

因此，電壓到電流轉換器的輸出電流 $I_{0}$ 等於其輸入電壓 $V_{i}$ 與電阻 $R_{1}$ 的比值。

我們可以將上述方程改寫為：

$$\frac{I_0}{V_i}=\frac{1}{R_1}$$

上述方程表示輸出電流 $I_{0}$ 與輸入電壓 $V_{i}$ 的比值，它等於電阻 $R_{1}$ 的倒數。輸出電流 $I_{0}$ 與輸入電壓 $V_{i}$ 的比值稱為跨導。

我們知道，電路輸出與輸入的比值稱為增益。因此，電壓到電流轉換器的增益就是跨導，它等於電阻 $R_{1}$ 的倒數。

電流到電壓轉換器

電流到電壓轉換器或I到V轉換器是一種電子電路，它以電流作為輸入，併產生電壓作為輸出。本節討論基於運放的電流到電壓轉換器。

基於運放的電流到電壓轉換器在電流施加到其反相端時產生輸出電壓。基於運放的電流到電壓轉換器的電路圖如下所示。

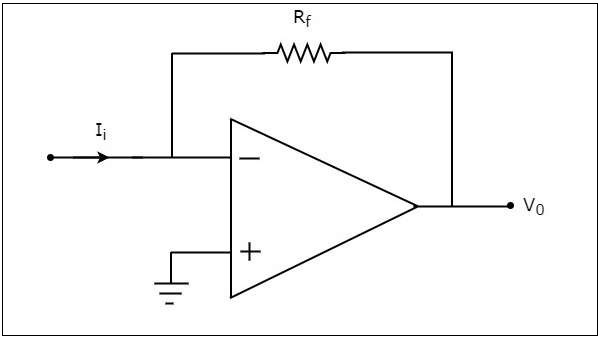
在上圖所示的電路中，運放的同相輸入端連線到地。這意味著在其同相輸入端施加了零伏特。

根據虛短概念，運放的反相輸入端的電壓將等於其同相輸入端的電壓。因此，運放的反相輸入端的電壓將為零伏特。

反相輸入端節點的節點方程為：

$$-I_{i}+\frac{0-V_0}{R_f}=0$$

$$-I_{i}=\frac{V_0}{R_f}$$

$$V_{0}=-R_{t}I_{i}$$

因此，電流到電壓轉換器的輸出電壓 $V_{0}$ 等於反饋電阻 $R_{f}$ 和輸入電流 $I_{t}$ 的（負）乘積。觀察到輸出電壓 $V_{0}$ 帶有負號，這表明輸入電流和輸出電壓之間存在 180⁰ 的相位差。

我們可以將上述方程改寫為：

$$\frac{V_0}{I_i}=-R_{f}$$

上述方程表示輸出電壓 $V_{0}$ 與輸入電流 $I_{i}$ 的比值，它等於反饋電阻 $R_{f}$ 的負值。輸出電壓 $V_{0}$ 與輸入電流 $I_{i}$ 的比值稱為跨阻。

我們知道，電路輸出與輸入的比值稱為增益。因此，電流到電壓轉換器的增益就是其跨阻，它等於（負）反饋電阻 $R_{f}$。

比較器

比較器是一種電子電路，它比較施加到其上的兩個輸入，併產生一個輸出。比較器的輸出值指示哪個輸入更大或更小。請注意，比較器屬於積體電路的非線性應用。

運放有兩個輸入端，因此基於運放的比較器比較施加到其上的兩個輸入，並將比較結果作為輸出。本章討論基於運放的比較器。

比較器的型別

比較器有兩種型別：反相和同相。本節將詳細討論這兩種型別。

反相比較器

反相比較器是一種基於運放的比較器，其參考電壓施加到其同相端，輸入電壓施加到其反相端。這種比較器被稱為反相比較器，因為要比較的輸入電壓施加到運放的反相端。

反相比較器的電路圖如下所示。

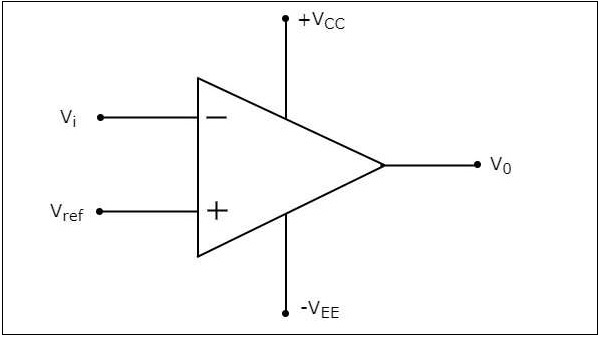
反相比較器的工作原理非常簡單。它根據輸入電壓 $V_{i}$ 和參考電壓 $V_{ref}$ 的值，在輸出端產生兩個值之一，$+V_{sat}$ 和 $-V_{sat}$。

當輸入 $V_{i}$ 電壓大於參考電壓 $V_{ref}$ 時，反相比較器的輸出值為 $-V_{sat}$。
當輸入 $V_{i}$ 小於參考電壓 $V_{ref}$ 時，反相比較器的輸出值為 $+V_{sat}$。

示例

讓我們繪製反相比較器的輸出波形，當正弦輸入訊號和零伏特的參考電壓分別施加到其反相端和同相端時。

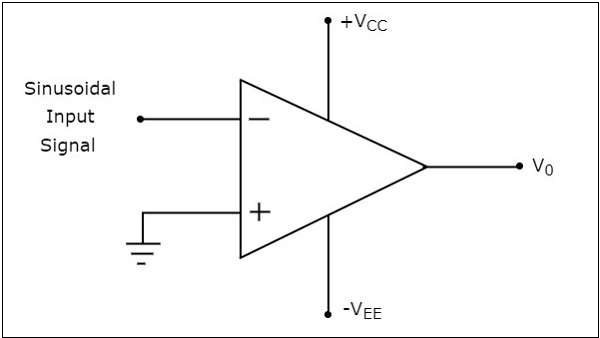
下面討論上圖所示的反相比較器的工作原理：

在正弦輸入訊號的正半週期期間，運放反相端存在的電壓大於零伏特。因此，在正弦輸入訊號的正半週期期間，反相比較器的輸出值將等於 $-V_{sat}$。
類似地，在正弦輸入訊號的負半週期期間，運放反相端存在的電壓小於零伏特。因此，在正弦輸入訊號的負半週期期間，反相比較器的輸出值將等於 $+V_{sat}$。

下圖顯示了當參考電壓為零伏特時，反相比較器的輸入和輸出波形。

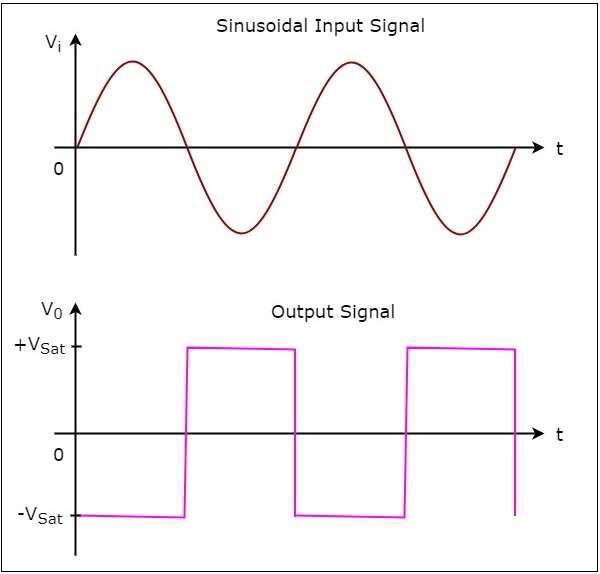
在上圖中，我們可以觀察到，每當正弦輸入訊號過零時，輸出都會從 $-V_{sat}$ 轉換到 $+V_{sat}$ 或從 $+V_{sat}$ 轉換到 $-V_{sat}$。換句話說，當輸入過零時，輸出會改變其值。因此，上述電路也稱為反相過零檢測器。

同相比較器

同相比較器是一種基於運放的比較器，其參考電壓施加到其反相端，輸入電壓施加到其同相端。這種基於運放的比較器被稱為同相比較器，因為要比較的輸入電壓施加到運放的同相端。

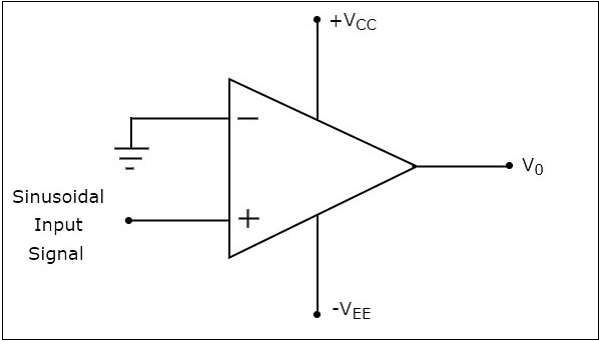
同相比較器的電路圖如下所示。

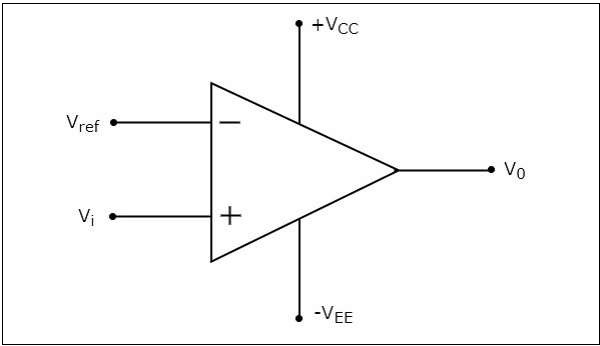
同相比較器的工作原理非常簡單。它根據輸入電壓 $V_{t}$ 和參考電壓 $+V_{ref}$ 的值，在輸出端產生兩個值之一，$+V_{sat}$ 和 $-V_{sat}$。

當輸入電壓 $V_{i}$ 大於參考電壓 $+V_{ref}$ 時，同相比較器的輸出值為 $+V_{sat}$。
當輸入電壓 $V_{i}$ 小於參考電壓 $+V_{ref}$ 時，同相比較器的輸出值為 $-V_{sat}$。

示例

讓我們繪製同相比較器的輸出波形，當正弦輸入訊號和零伏特的參考電壓分別施加到運放的同相端和反相端時。

下面解釋同相比較器的工作原理：

在正弦輸入訊號的正半週期期間，運放同相端存在的電壓大於零伏特。因此，在正弦輸入訊號的正半週期期間，同相比較器的輸出值將等於 $+V_{sat}$。
類似地，在正弦輸入訊號的負半週期期間，運放同相端存在的電壓小於零伏特。因此，在正弦輸入訊號的負半週期期間，同相比較器的輸出值將等於 $-V_{sat}$。

下圖顯示了當參考電壓為零伏特時，同相比較器的輸入和輸出波形。

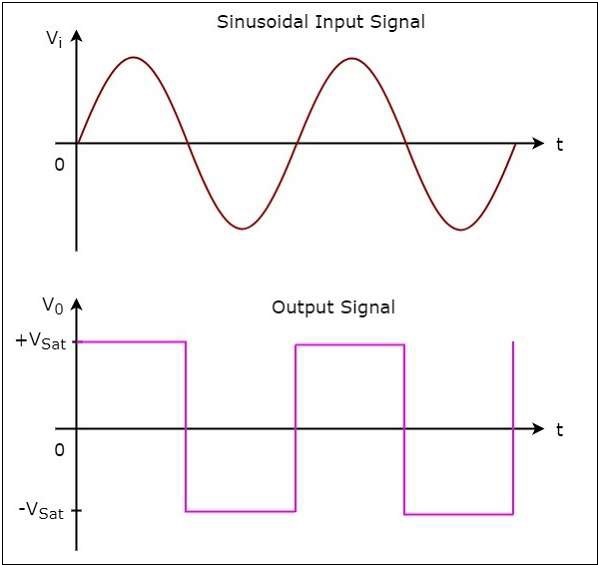
從上圖可以看出，每當正弦輸入訊號過零時，輸出都會從 $+V_{sat}$ 轉換到 $-V_{sat}$ 或從 $-V_{sat}$ 轉換到 $+V_{sat}$。這意味著，當輸入過零時，輸出會改變其值。因此，上述電路也稱為同相過零檢測器。

對數和反對數放大器

執行對數和反對數（指數）等數學運算並進行放大的電子電路分別稱為對數放大器和反對數放大器。

本章將詳細討論對數放大器和反對數放大器。請注意，這些放大器屬於非線性應用。

對數放大器

對數放大器或對數放大器是一種電子電路，它產生與施加的輸入的對數成正比的輸出。本節將詳細討論基於運放的對數放大器。

基於運放的對數放大器在輸出端產生一個電壓，該電壓與施加到連線到其反相端的電阻上的電壓的對數成正比。基於運放的對數放大器的電路圖如下所示：

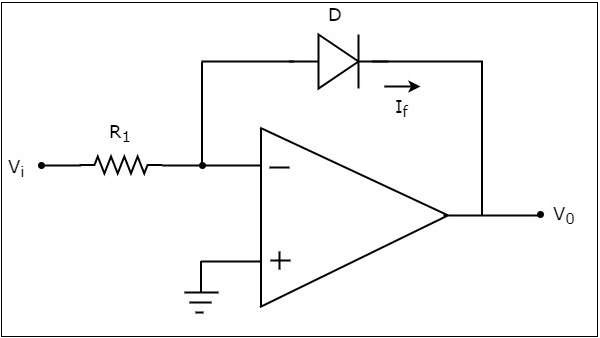
在上圖電路中，運放的同相輸入端連線到地。這意味著在運放的同相輸入端施加了零伏特。

根據虛短概念，運算放大器的反相輸入端電壓等於其同相輸入端電壓。因此，反相輸入端電壓將為零伏。

反相輸入端節點的節點方程為：

$$\frac{0-V_i}{R_1}+I_{f}=0$$

$$=>I_{f}=\frac{V_i}{R_1}......公式1$$

以下是二極體正向偏置時電流方程：

$$I_{f}=I_{s} e^{(\frac{V_f}{nV_T})} ......公式2$$

其中，

$I_{s}$ 是二極體的飽和電流，

$V_{f}$ 是二極體正向偏置時的壓降，

$V_{T}$ 是二極體的熱等效電壓。

運算放大器反饋環路的KVL方程為：

$$0-V_{f}-V_{0}=0$$

$$=>V_{f}=-V_{0}$$

將$V_{f}$的值代入公式2，得到：

$$I_{f}=I_{s} e^{\left(\frac{-V_0}{nV_T}\right)} ......公式3$$

觀察公式1和公式3的左側項相同。因此，將這兩個公式的右側項等同起來，如下所示：

$$\frac{V_i}{R_1}=I_{s}e^{\left(\frac{-V_0}{nV_T}\right)}$$

$$\frac{V_i}{R_1I_s}= e^{\left(\frac{-V_0}{nV_T}\right)}$$

在兩邊應用自然對數，得到：

$$In\left(\frac{V_i}{R_1I_s}\right)= \frac{-V_0}{nV_T}$$

$$V_{0}=-{nV_T}In\left(\frac{V_i}{R_1I_s}\right)$$

注意，在上式中，引數n，${V_T}$和$I_{s}$是常數。因此，對於固定電阻值$R_{1}$，輸出電壓$V_{0}$將與輸入電壓$V_{i}$的自然對數成正比。

因此，上述基於運算放大器的對數放大器電路將在${R_1I_s}=1V$時產生與輸入電壓${V_T}$的自然對數成正比的輸出。

觀察到輸出電壓$V_{0}$帶有一個負號，這表明輸入和輸出之間存在180⁰的相位差。

反對數放大器

反對數放大器是一種電子電路，它產生的輸出與施加的輸入的反對數成正比。本節詳細討論了基於運算放大器的反對數放大器。

基於運算放大器的反對數放大器在輸出端產生一個電壓，該電壓與施加到連線到其反相輸入端的二極體的電壓的反對數成正比。

基於運算放大器的反對數放大器的電路圖如下所示：

在上圖所示的電路中，運算放大器的同相輸入端連線到地。這意味著零伏被施加到其同相輸入端。

根據虛短概念，運算放大器的反相輸入端電壓等於其同相輸入端電壓。因此，其反相輸入端電壓將為零伏。

反相輸入端節點的節點方程為：

$$-I_{f}+\frac{0-V_0}{R_f}=0$$

$$=>-\frac{V_0}{R_f}=I_{f}$$

$$=>V_{0}=-R_{f}I_{f}.........公式4$$

我們知道，二極體正向偏置時流過二極體的電流方程如下所示：

$$I_{f}=I_{s} e^{\left(\frac{V_f}{nV_T}\right)}$$

將$I_{f}$的值代入公式4，得到

$$V_{0}=-R_{f}\left \{{I_{s} e^{\left(\frac{V_f}{nV_T}\right)}}\right \}$$

$$V_{0}=-R_{f}{I_{s} e^{\left(\frac{V_f}{nV_T}\right)}}......公式5$$

運算放大器反相輸入端的輸入側的KVL方程為

$$V_{i}-V_{f}=0$$

$$V_{f}=V_{i}$$

將𝑉𝑓的值代入公式5，得到：

$$V_{0}=-R_{f}{I_{s} e^{\left(\frac{V_i}{nV_T}\right)}}$$

注意，在上式中，引數n，${V_T}$和$I_{s}$是常數。因此，對於固定反饋電阻${R_f}$，輸出電壓${V_0}$將與輸入電壓${V_i}$的反自然對數（指數）成正比。

因此，上述基於運算放大器的反對數放大器電路將在${R_fI_s}= 1V$時產生與輸入電壓${V_i}$的反自然對數（指數）成正比的輸出。觀察到輸出電壓${V_0}$帶有一個負號，這表明輸入和輸出之間存在180⁰的相位差。

整流器

交流電和直流電是在學習電荷流動時遇到的兩個常見術語。交流電（AC）具有持續改變其狀態的特性。例如，如果我們考慮正弦波，則電流在正半週期內沿一個方向流動，在負半週期內沿相反方向流動。另一方面，直流電（DC）僅沿一個方向流動。

當施加交流訊號時，產生直流訊號或脈衝直流訊號的電子電路稱為整流器。本章詳細討論了基於運算放大器的整流器。

整流器的型別

整流器分為兩種型別：半波整流器和全波整流器。本節詳細討論這兩種型別。

半波整流器

半波整流器是一種整流器，它在輸入的一個半週期內在輸出端產生正半週期，在輸入的另一個半週期內輸出為零。

半波整流器的電路圖如下所示。

觀察到，上面所示的半波整流器電路圖看起來像一個反相放大器，另外還有兩個二極體D₁和D₂。

下面解釋上面所示的半波整流器電路的工作原理

對於正弦輸入的正半週期，運算放大器的輸出將為負。因此，二極體D₁將被正向偏置。
當二極體D₁正向偏置時，運算放大器的輸出電壓將為-0.7 V。因此，二極體D₂將被反向偏置。因此，上述電路的輸出電壓為零伏。
因此，對於正弦輸入的正半週期，半波整流器沒有（零）輸出。
對於正弦輸入的負半週期，運算放大器的輸出將為正。因此，二極體D₁和D₂將分別被反向偏置和正向偏置。因此，上述電路的輸出電壓將為：

$$V_0=-\left(\frac{R_f}{R_1}\right)V_1$$

因此，半波整流器的輸出將是正弦輸入負半週期的正半週期。

波形

半波整流器的輸入和輸出波形如下所示

從上圖可以看出，我們討論的半波整流器電路圖將為正弦輸入的負半週期產生正半週期，併為正弦輸入的正半週期產生零輸出

全波整流器

全波整流器在輸入的兩個半週期內都在輸出端產生正半週期。

電路圖如下所示：

上述電路圖由兩個運算放大器、兩個二極體D₁和D₂以及五個電阻R₁到R₅組成。下面解釋上面所示的全波整流器電路的工作原理：

對於正弦輸入的正半週期，第一個運算放大器的輸出將為負。因此，二極體D₁和D₂將分別被正向偏置和反向偏置。
然後，第一個運算放大器的輸出電壓將為：

$$V_{01}=-\left(\frac{R_2}{R_1}\right)V_i$$

觀察到第一個運算放大器的輸出連線到電阻R₄，該電阻連線到第二個運算放大器的反相輸入端。第二個運算放大器的同相輸入端電壓為0 V。因此，第二個運算放大器與電阻R₄和R₄一起充當反相放大器。
第二個運算放大器的輸出電壓將為

$$V_0=-\left(\frac{R_5}{R_4}\right)V_{01}$$

代入上述方程中的$V_{01}$的值，得到：

$$=>V_{0}=-\left(\frac{R_5}{R_4}\right)\left \{ -\left(\frac{R_2}{R_1}\right)V_{i} \right \}$$

$$=>V_{0}=\left(\frac{R_2R_5}{R_1R_4}\right)V_{i}$$
因此，全波整流器的輸出將是正弦輸入正半週期的正半週期。在這種情況下，輸出的增益為$\frac{R_2R_5}{R_1R_4}$。如果我們考慮$R_{1}=R_{2}=R_{4}=R_{5}=R$，則輸出的增益將為1。
對於正弦輸入的負半週期，第一個運算放大器的輸出將為正。因此，二極體D₁和D₂將分別被反向偏置和正向偏置。
第一個運算放大器的輸出電壓將為：

$$V_{01}=-\left(\frac{R_3}{R_1}\right)V_{i}$$

第一個運算放大器的輸出直接連線到第二個運算放大器的同相輸入端。現在，第二個運算放大器與電阻R₄和R₅一起充當同相放大器。

第二個運算放大器的輸出電壓將為：

$$V_{0}=\left(1+\frac{R_5}{R_4}\right)V_{01}$$

代入上述方程中的$V_{01}$的值，得到

$$=>V_{0}=\left(1+\frac{R_5}{R_4}\right) \left\{-\left(\frac{R_3}{R_1}\right)V_{i}\right \} $$

$$=>V_{0}=-\left(\frac{R_3}{R_1}\right)\left(1+\frac{R_5}{R_4}\right)V_{i}$$
因此，全波整流器的輸出也將是正弦輸入負半週期的正半週期。在這種情況下，輸出增益的大小為$\left(\frac{R_3}{R_1}\right)\left(1+\frac{R_5}{R_4}\right)$。如果我們考慮$R_{1}=2R_{3}=R_{4}=R_{5}=R$，則輸出的增益將為1。

輸入和輸出波形如下所示

如上圖所示，我們考慮的全波整流器電路圖將僅為正弦輸入的正負半週期都產生正半週期。

削波器

波形整形電路是能夠根據輸入波形產生所需輸出波形的電子電路。這些電路主要執行兩個功能：

衰減輸入波形
改變輸入波形的直流電平。

波形整形電路主要分為兩種型別：削波器和鉗位器。本章將詳細介紹削波器。

基於運放的削波器

削波器是一種電子電路，它透過去除輸入訊號中高於或低於參考值的某一部分來產生輸出。也就是說，除了被削波的部分之外，削波器的輸出與輸入相同。因此，削波器輸出的峰峰值始終小於輸入訊號的峰峰值。

削波器主要優點是可以消除交流訊號幅度中不需要的噪聲。

根據削波輸入訊號的部分，可以將削波器分為以下兩種型別：

正削波器
負削波器

下面將詳細介紹這兩種型別：

正削波器

正削波器是一種只削波輸入訊號正半部分（或部分）的削波器。

正削波器的電路圖如下所示：

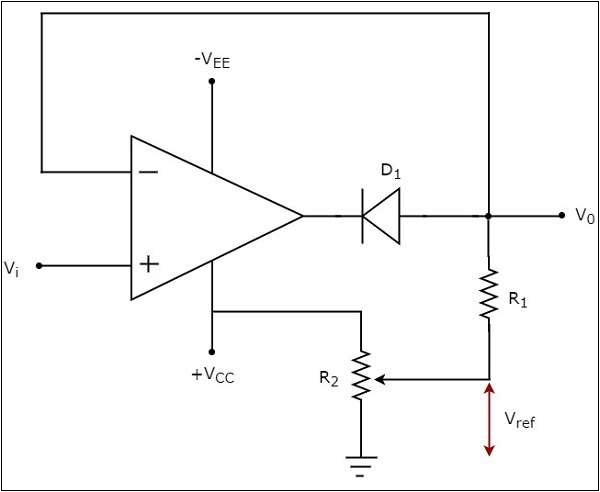
在上圖所示的電路中，正弦電壓訊號$V_{i}$被施加到運放的同相端。參考電壓$V_{ref}$的值可以透過改變電阻$R_{2}$來選擇。

上面所示電路的工作原理如下：

如果輸入電壓$V_i$的值小於參考電壓$V_{ref}$的值，則二極體D₁導通。此時，上述電路表現為電壓跟隨器。因此，當$V_{i}$ < $V_{ref}$時，上述電路的輸出電壓$V_{0}$與輸入電壓$V_{i}$相同。
如果輸入電壓$V_{i}$的值大於參考電壓$V_{ref}$的值，則二極體D₁截止。由於反饋路徑斷開，運放現在處於開環狀態。因此，當$V_{i}$ > $V_{ref}$時，上述電路的輸出電壓$V_{0}$將等於參考電壓$V_{ref}$的值。

對於正參考電壓$V_{ref}$，正削波器的輸入波形和相應的輸出波形如下所示：

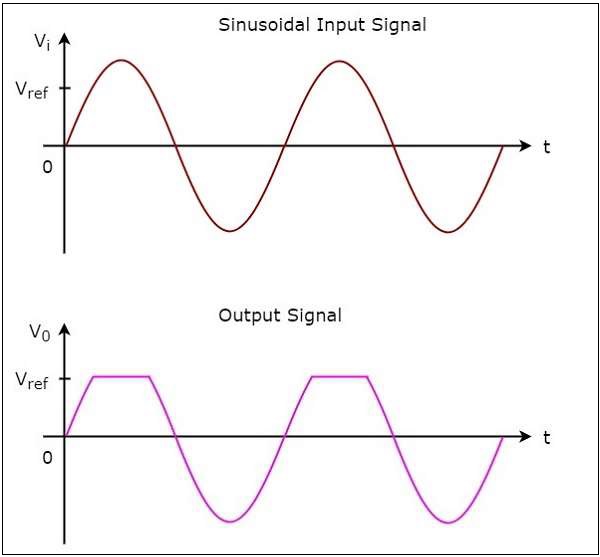
負削波器

負削波器是一種只削波輸入訊號負半部分（或部分）的削波器。可以透過在正削波器的電路中反轉二極體並取參考電壓的反極性來獲得負削波器的電路。

負削波器的電路圖如下所示：

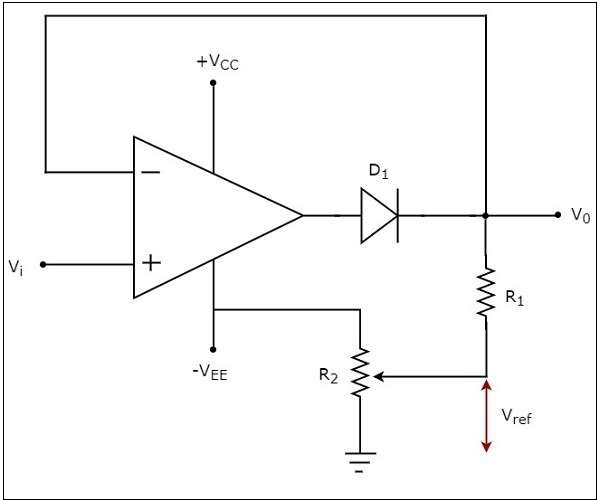
在上圖所示的電路中，正弦電壓訊號$V_{i}$被施加到運放的同相端。參考電壓$V_{ref}$的值可以透過改變電阻$R_{2}$來選擇。

負削波器電路的工作原理如下：

如果輸入電壓$V_{i}$的值大於參考電壓$V_{ref}$的值，則二極體D₁導通。此時，上述電路表現為電壓跟隨器。因此，當$V_{i}$> $V_{ref}$時，上述電路的輸出電壓$V_{0}$與輸入電壓$V_{i}$相同。

如果輸入電壓$V_{i}$的值小於參考電壓的值，則二極體D₁截止。由於反饋路徑斷開，運放現在處於開環狀態。因此，當$V_{i}$ < $V_{ref}$時，上述電路的輸出電壓$V_{0}$將等於參考電壓$V_{ref}$的值。

對於負參考電壓$V_{ref}$，負削波器的輸入波形和相應的輸出波形如下所示：

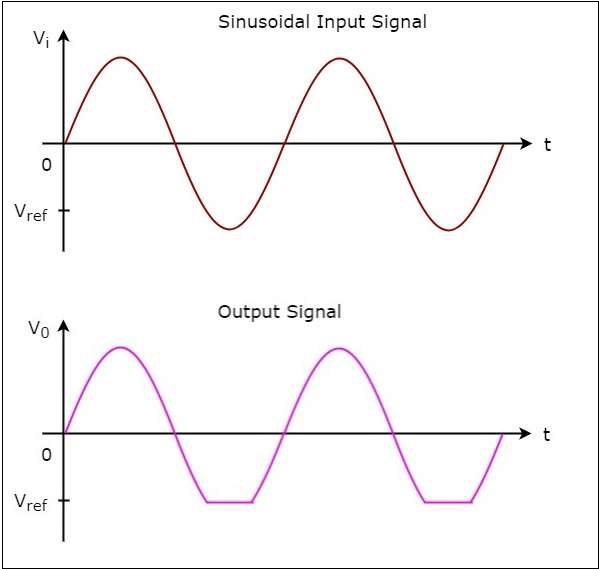
鉗位器

在上一章中，我們討論了削波器。現在，讓我們討論另一種型別的波形整形電路，即鉗位器。

基於運放的鉗位器

鉗位器是一種電子電路，它產生的輸出與輸入相似，但直流電平發生了偏移。換句話說，鉗位器的輸出是輸入的精確複製。因此，鉗位器輸出的峰峰值始終等於輸入的峰峰值。

鉗位器用於在輸出端引入或恢復輸入訊號的直流電平。根據輸入訊號的直流偏移，基於運放的鉗位器有兩種型別。

正鉗位器
負鉗位器

本節將詳細討論這兩種型別的鉗位器。

正鉗位器

正鉗位器是一種鉗位電路，它以使輸入訊號在垂直方向上發生正直流偏移的方式產生輸出。

電路圖如下所示：

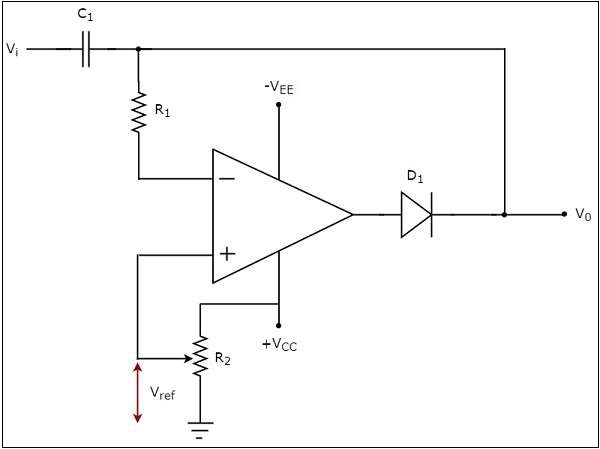
在上圖所示的電路中，正弦電壓訊號$V_{i}$透過由電容$C_{1}$和電阻$R_{1}$組成的網路施加到運放的反相端。也就是說，交流電壓訊號被施加到運放的反相端。

直流參考電壓$V_{ref}$被施加到運放的同相端。參考電壓$V_{ref}$的值可以透過改變電阻$R_{2}$來選擇。在這種情況下，我們將得到一個正值的參考電壓$V_{ref}$。

上述電路產生的輸出是正弦電壓訊號$V_{i}$和參考電壓$V_{ref}$的組合（疊加）。也就是說，鉗位電路以使正弦電壓訊號$V_{i}$在垂直方向上向上偏移參考電壓$V_{ref}$的值的方式產生輸出。

正鉗位器的輸入波形和相應的輸出波形如下所示：

從上圖可以看出，正鉗位器在輸出端使施加的輸入波形垂直向上偏移。偏移量將取決於直流參考電壓的值。

負鉗位器

負鉗位器是一種鉗位電路，它以使輸入訊號在垂直方向上發生負直流偏移的方式產生輸出。

電路圖如下所示：

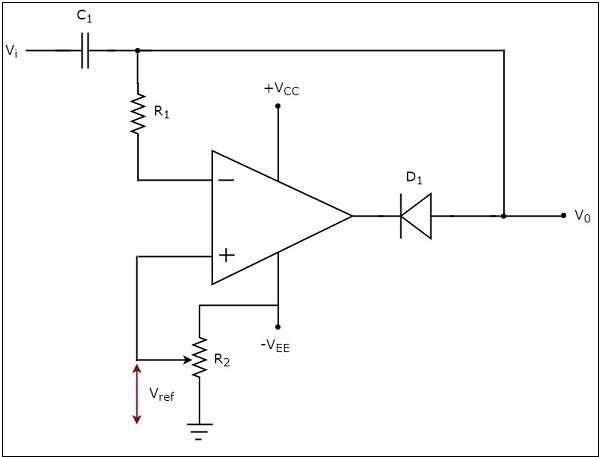
在上圖所示的電路中，正弦電壓訊號$V_{i}$透過由電容C₁和電阻$R_{1}$組成的網路施加到運放的反相端。也就是說，交流電壓訊號被施加到運放的反相端。

直流參考電壓$V_{ref}$被施加到運放的同相端。參考電壓$V_{ref}$的值可以透過改變電阻$R_{2}$來選擇。在這種情況下，我們將得到一個負值的參考電壓$V_{ref}$。

上述電路產生的輸出是正弦電壓訊號$V_{i}$和參考電壓$V_{ref}$的組合（疊加）。也就是說，鉗位電路以使正弦電壓訊號$V_{i}$在垂直方向上向下偏移參考電壓$V_{ref}$的值的方式產生輸出。

負鉗位器的輸入波形和相應的輸出波形如下所示：

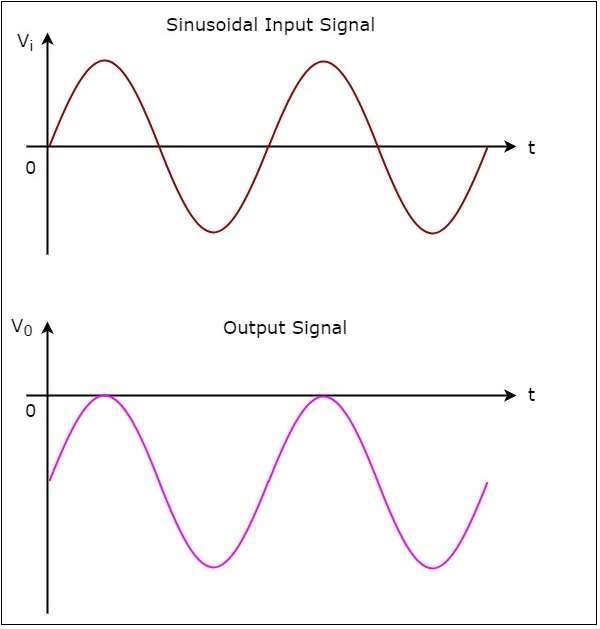
從輸出可以看出，負鉗位器在輸出端使施加的輸入波形垂直向下偏移。偏移量將取決於直流參考電壓的值。

有源濾波器

濾波器是一種允許某些頻率成分透過並/或抑制其他頻率成分的電子電路。您可能在網路理論教程中遇到過濾波器。它們是被動的，並且是包含無源元件（如電阻、電容和/或電感）的電子電路或網路。

本章將詳細討論有源濾波器。

有源濾波器的型別

有源濾波器是包含有源元件（如運放）以及無源元件（如電阻和電容）的電子電路。

根據它們允許和/或抑制的頻率範圍，有源濾波器主要分為以下四種類型：

有源低通濾波器
有源高通濾波器
有源帶通濾波器
有源帶阻濾波器

有源低通濾波器

如果一個有源濾波器只允許（透過）低頻成分並抑制（阻擋）所有其他高頻成分，則稱為有源低通濾波器。

有源低通濾波器的電路圖如下所示：

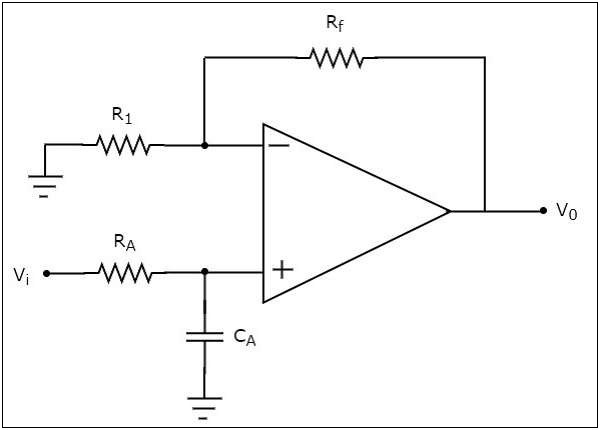
我們知道，連線到運放同相端的電網路是一個無源低通濾波器。因此，運放同相端的輸入是無源低通濾波器的輸出。

觀察到上述電路類似於同相放大器。它將無源低通濾波器的輸出作為運放同相端的輸入。因此，它產生的輸出是其同相端輸入的$\left(1+\frac{R_f}{R_1}\right)$倍。

我們可以適當地選擇$R_{f}$和$R_{1}$的值以獲得輸出端的所需增益。例如，如果我們將$R_{f}$和$R_{1}$的電阻值分別視為零歐姆和無窮大歐姆，則上述電路將產生一個單位增益的低通濾波器輸出。

有源高通濾波器

如果一個有源濾波器只允許（透過）高頻成分並抑制（阻擋）所有其他低頻成分，則稱為有源高通濾波器。

有源高通濾波器的電路圖如下所示：

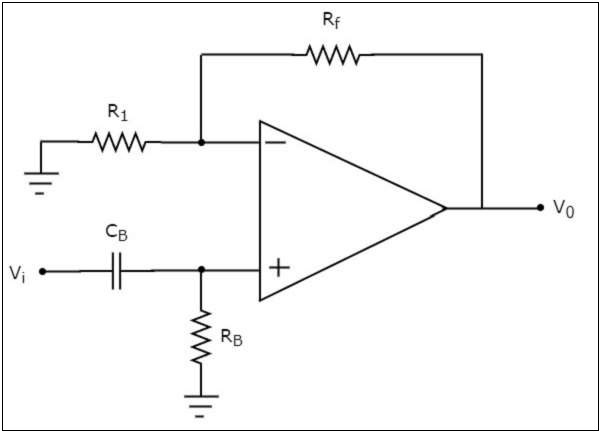
我們知道，連線到運放同相端的電網路是一個無源高通濾波器。因此，運放同相端的輸入是無源高通濾波器的輸出。

現在，上述電路類似於同相放大器。它將無源高通濾波器的輸出作為運放同相端的輸入。因此，它產生的輸出是其同相端輸入的$\left(1+\frac{R_f}{R_1}\right)$倍。

我們可以適當地選擇$R_f$和$R_1$的值以獲得輸出端的所需增益。例如，如果我們將$R_{f}$和$R_{1}$的電阻值分別視為零歐姆和無窮大歐姆，則上述電路將產生一個單位增益的高通濾波器輸出。

有源帶通濾波器

如果一個有源濾波器只允許（透過）一個頻帶，則稱為有源帶通濾波器。通常，該頻帶位於低頻範圍和高頻範圍之間。因此，有源帶通濾波器抑制（阻擋）低頻和高頻成分。

有源帶通濾波器的電路圖如下所示：

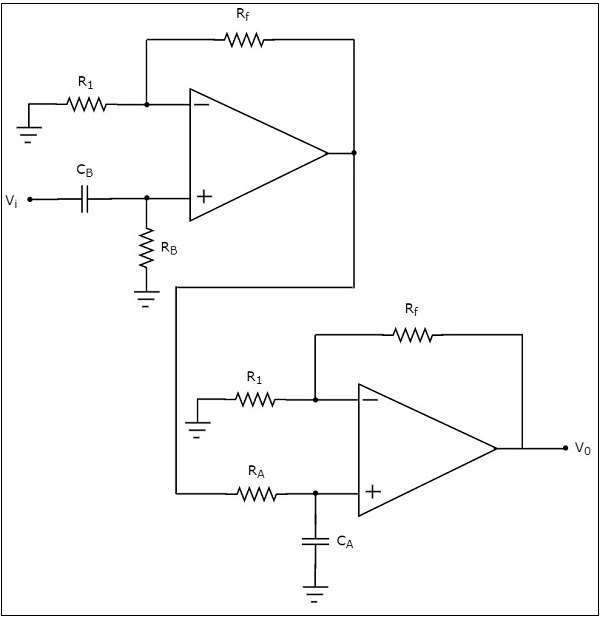
觀察到有源帶通濾波器的電路圖中有兩部分：第一部分是有源高通濾波器，第二部分是有源低通濾波器。

有源高通濾波器的輸出作為有源低通濾波器的輸入。也就是說，為了獲得只包含特定頻帶的輸出，有源高通濾波器和有源低通濾波器是級聯的。

第一級存在的**主動高通濾波器**允許頻率高於主動帶通濾波器的**下截止頻率**。因此，我們必須適當地選擇$R_{B}$和$C_{B}$的值，以獲得主動帶通濾波器所需的**下截止頻率**。

類似地，第二級存在的**主動低通濾波器**允許頻率小於主動帶通濾波器的高截止頻率。因此，我們必須適當地選擇$R_{A}$和$C_{A}$的值，以獲得主動帶通濾波器所需的**高截止頻率**。

因此，上面討論的圖中的電路將產生一個主動帶通濾波器輸出。

有源帶阻濾波器

如果一個有源濾波器抑制（阻擋）特定頻段的頻率，則稱為**主動帶阻濾波器**。通常，此頻段位於低頻範圍和高頻範圍之間。因此，主動帶阻濾波器允許（透過）低頻和高頻分量。

主動帶阻濾波器的**框圖**如下所示：

觀察到，主動帶阻濾波器的框圖在其第一級包含兩個模組：一個主動低通濾波器和一個主動高通濾波器。這兩個模組的輸出作為輸入應用於第二級存在的模組。因此，**加法放大器**產生一個輸出，該輸出是主動低通濾波器和主動高通濾波器輸出之和的放大版本。

因此，當我們選擇低通濾波器的截止頻率小於高通濾波器的截止頻率時，上述框圖的輸出將是**主動帶阻濾波器的輸出**。

主動帶阻濾波器的**電路圖**如下所示：

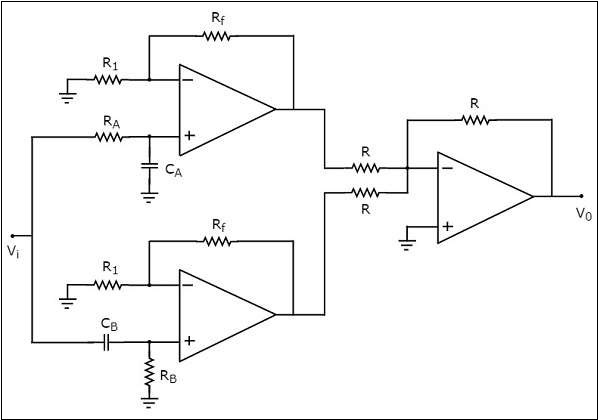
我們已經看到了主動低通濾波器、主動高通濾波器和加法放大器的電路圖。觀察到，我們透過在主動帶阻濾波器的框圖中用相應的電路圖替換模組，得到了上述主動帶阻濾波器的**電路圖**。

正弦波振盪器

振盪器是一種產生週期性訊號的電子電路。如果振盪器產生正弦振盪，則稱為**正弦振盪器**。它將來自直流電源的輸入能量轉換為週期性訊號的交流輸出能量。此週期性訊號將具有特定的頻率和幅度。

正弦振盪器的**框圖**如下所示：

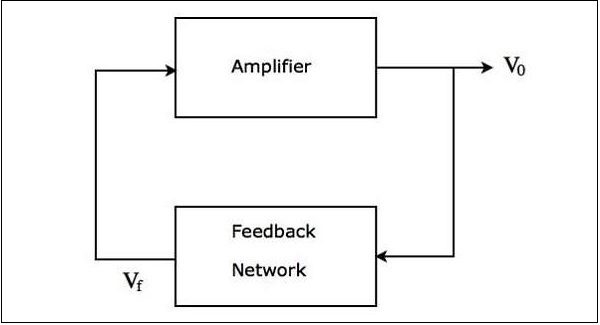
上圖主要包含**兩個模組**：一個放大器和一個反饋網路。反饋網路將放大器輸出的一部分作為輸入，併產生電壓訊號。此電壓訊號作為輸入應用於放大器。

當滿足以下**兩個條件**時，上面所示的正弦振盪器框圖將產生正弦振盪：

上述正弦振盪器框圖的**環路增益**$A_{v}\beta$必須大於或等於**1**。這裡，$A_{v}$和$\beta$分別是放大器的增益和反饋網路的增益。
上述正弦振盪器框圖環路的總**相移**必須為**0⁰**或**360⁰**。

上述兩個條件一起被稱為**巴克豪森準則**。

基於運放的振盪器

有**兩種**型別的基於運放的振盪器。

RC移相振盪器
維恩電橋振盪器

本節將詳細討論它們。

RC移相振盪器

基於運放的振盪器，它藉助反相放大器和反饋網路在輸出端產生正弦電壓訊號，被稱為**RC移相振盪器**。此反饋網路由三個級聯的RC網路組成。

**電路圖**如下所示：

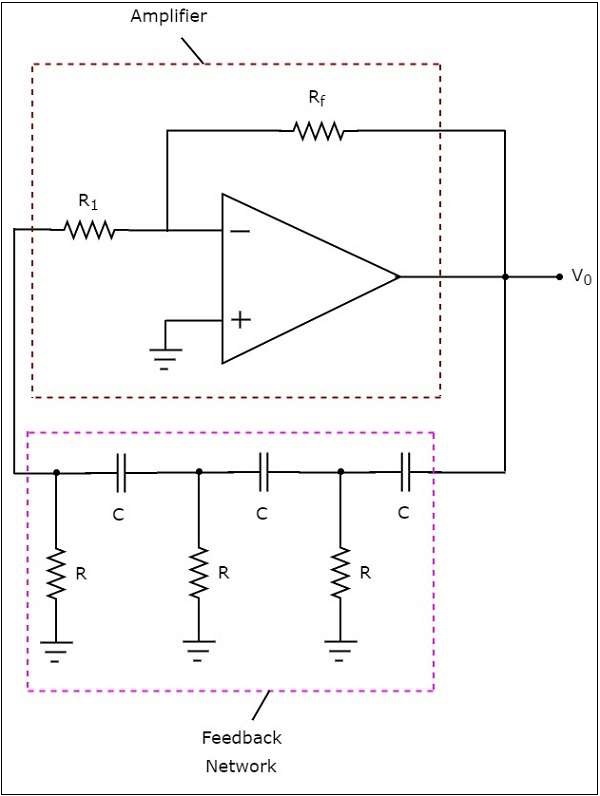
在上述電路中，運放工作在**反相模式**。因此，它提供180⁰的相移。上述電路中存在的反饋網路也提供180⁰的相移，因為每個RC網路提供60⁰的相移。因此，上述電路在某個頻率下提供360⁰的總相移。

RC移相振盪器的**輸出頻率**為：

$$f=\frac{1}{2\Pi RC\sqrt[]{6}}$$

反相放大器的**增益$A_{v}$**應大於或等於-29，

$$i.e.,-\frac{R_f}{R_1}\geq-29$$

$$=>\frac{R_f}{R_1}\geq-29$$

$$=>R_{f}\geq29R_{1}$$

因此，為了在RC移相振盪器的輸出端產生持續振盪，我們應該將反饋電阻$R_{f}$的值考慮為電阻$R_{1}$值的至少29倍。

維恩電橋振盪器

基於運放的振盪器，它藉助同相放大器和反饋網路在輸出端產生正弦電壓訊號，被稱為**維恩電橋振盪器**。

**電路圖**如下所示：

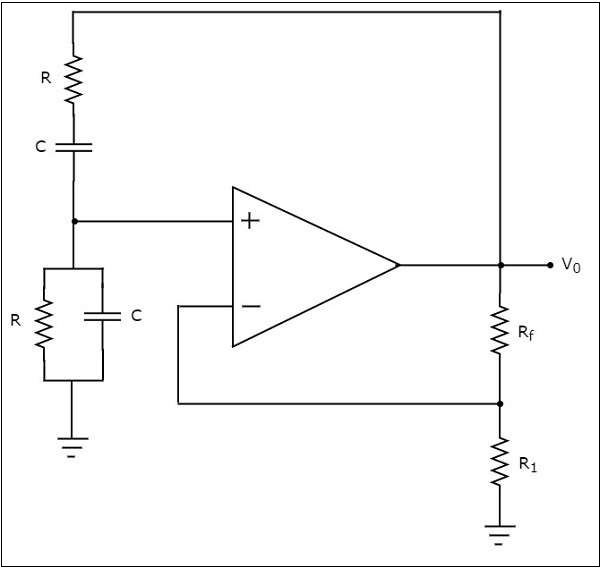
在上面所示的維恩電橋振盪器電路中，運放工作在**同相模式**。因此，它提供00的相移。所以，上述電路中存在的反饋網路不應該提供任何相移。

如果反饋網路提供一些相移，則我們必須**平衡電橋**，以使不存在任何相移。因此，上述電路在某個頻率下提供0⁰的總相移。

維恩電橋振盪器的**輸出頻率**為

$$f=\frac{1}{2\Pi RC}$$

同相放大器的**增益$A_{v}$**應大於或等於3

$$i.e.,1+\frac{R_f}{R_1}\geq3$$

$$=>\frac{R_f}{R_1}\geq2$$

$$=>R_{f}\geq2R_{1}$$

因此，為了在維恩電橋振盪器的輸出端產生持續振盪，我們應該將反饋電阻$R_{f}$的值考慮為電阻$R_{1}$值的至少兩倍。

波形發生器

**波形發生器**是一種電子電路，它產生標準波形。有兩種型別的基於運放的波形發生器：

方波發生器
三角波發生器

本章將詳細討論這些基於運放的波形發生器。

方波發生器

**方波發生器**是一種產生方波的電子電路。本節討論基於運放的方波發生器。

基於運放的方波發生器的**電路圖**如下所示

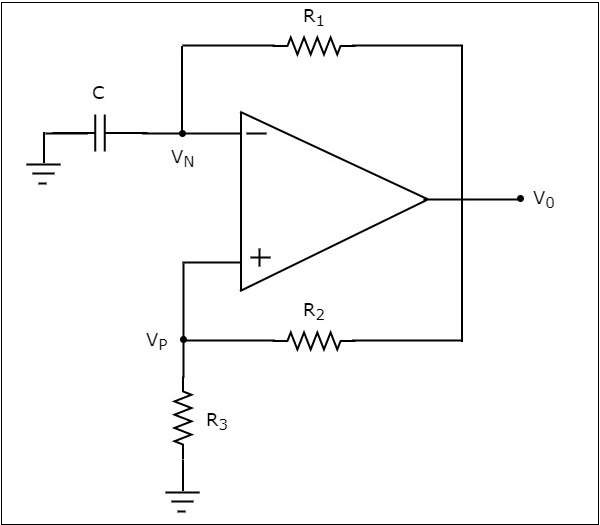
觀察到，在上面所示的電路圖中，電阻$R_{1}$連線在運放的反相輸入端與其輸出之間。因此，電阻$R_{1}$用於**負反饋**。類似地，電阻$R_{2}$連線在運放的同相輸入端與其輸出之間。因此，電阻$R_{2}$用於**正反饋**路徑。

電容器C連線在運放的反相輸入端和地之間。因此，**電容器C兩端的電壓**將是運放此反相輸入端的輸入電壓。類似地，電阻$R_{3}$連線在運放的同相輸入端和地之間。因此，**電阻$R_{3}$兩端的電壓**將是運放此同相輸入端的輸入電壓。

下面解釋**方波發生器的操作**：

假設最初電容器中**沒有電荷**。然後，運放反相輸入端存在的電壓為零伏。但是，運放同相輸入端存在一些偏移電壓。由於此原因，上述電路輸出端存在的值將為$+V_{sat}$。
現在，電容器C開始透過電阻$R_{1}$**充電**。當電容器C兩端的電壓達到略大於電阻$R_{3}$兩端的電壓（正值）時，上述電路輸出端存在的值將變為$-V_{sat}$。
當上述電路的輸出為$-V_{sat}$時，電容器C開始透過電阻$R_{1}$**放電**。當電容器C兩端的電壓達到略小於（更負）電阻$R_{3}$兩端的電壓（負值）時，上述電路輸出端存在的值將變為$+V_{sat}$。

因此，上面圖中所示的電路將在輸出端產生一個**方波**，如下所示：

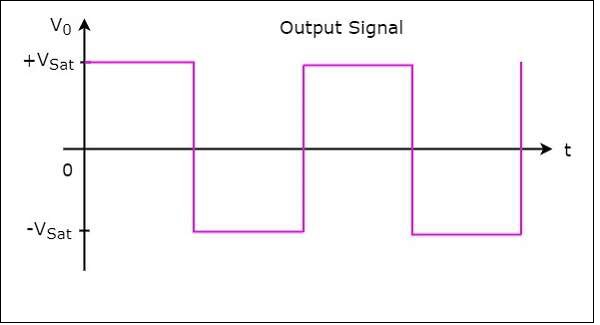
從上圖我們可以觀察到，方波發生器的輸出將具有兩個值之一：$+V_{sat}$和$-V_{sat}$。因此，輸出在某個持續時間內保持一個值，然後過渡到另一個值並在那裡保持某個持續時間。就這樣持續下去。

三角波發生器

三角波發生器是一種產生三角波的電子電路。**框圖**如下所示：

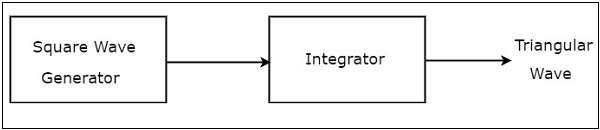
三角波發生器的框圖主要包含兩個模組：一個方波發生器和一個積分器。這兩個模組是**級聯**的。這意味著方波發生器的輸出作為積分器的輸入。請注意，方波的積分不過是三角波。

基於運放的三角波發生器的**電路圖**如下所示：

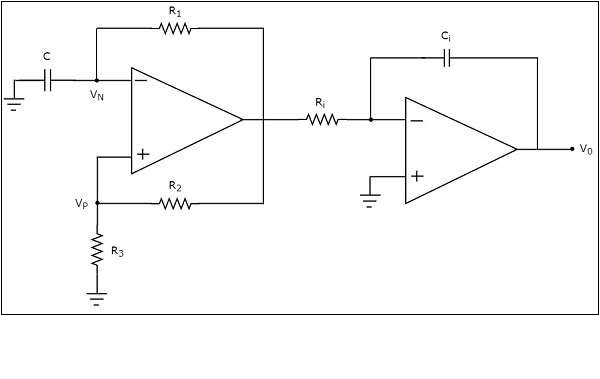
我們已經看到了方波發生器和積分器的電路圖。觀察到，我們透過在三角波發生器的框圖中用相應的電路圖替換模組，得到了上面基於運放的三角波發生器的**電路圖**。

555定時器

**555定時器**IC的名字來源於其分壓網路中使用的三個$5K\Omega$電阻。此IC可用於產生精確的時間延遲和振盪。本章將詳細介紹555定時器。

引腳圖和功能圖

在本節中，首先讓我們討論555定時器IC的引腳圖，然後討論其功能圖。

引腳圖

555定時器IC是一個8引腳迷你雙列直插封裝（DIP）。**引腳圖**如下所示：

從上圖可以看出每個引腳的意義不言而喻。此555定時器IC可以使用+5V至+18V的直流電源供電。它主要用於產生**非正弦**波形，如方波、斜坡波、脈衝等

功能圖

顯示555定時器內部細節的圖形表示稱為功能圖。

**功能圖**如下所示：

觀察到，555定時器的功能圖包含一個分壓網路、兩個比較器、一個SR觸發器、兩個電晶體和一個反相器。本節將詳細討論每個模組或元件的目的：

分壓網路

分壓網路由三個串聯連線在電源電壓$V_{cc}$和地之間的$5K\Omega$電阻組成。
如果只有一個$5K\Omega$電阻，則此網路在一點和地之間提供$\frac{V_{cc} }{3}$的電壓。類似地，如果只有兩個$5K\Omega$電阻，則它在一點和地之間提供$\frac{2V_{cc} }{3}$的電壓。

比較器

555定時器IC的功能框圖由兩個比較器組成：一個上限比較器（UC）和一個下限比較器（LC）。
回顧一下，比較器比較施加在其上的兩個輸入併產生一個輸出。
如果運放的同相端電壓大於其反相端電壓，則比較器的輸出將為$+V_{sat}$。在數字表示中，這可以視為邏輯高（'1'）。
如果運放的同相端電壓小於或等於其反相端電壓，則比較器的輸出將為$-V_{sat}$。在數字表示中，這可以視為邏輯低（'0'）。

SR觸發器

回顧一下，SR觸發器以正時鐘沿或負時鐘沿工作。它有兩個輸入：S和R，以及兩個輸出：Q(t)和Q(t)'。輸出Q(t)和Q(t)'互為補碼。
下表顯示了SR觸發器的狀態表

S	R	Q(t+1)
0	0	Q(t)
0	1	0
1	0	1
1	1	-

這裡，Q(t)和Q(t+1)分別表示當前狀態和下一狀態。因此，根據輸入條件，當施加時鐘訊號的正（負）沿時，SR觸發器可用於三種功能之一，例如保持、復位和置位。
下限比較器（LC）和上限比較器（UC）的輸出作為SR觸發器的輸入，如555定時器IC的功能框圖所示。

電晶體和反相器

555定時器IC的功能框圖包含一個npn電晶體$Q_{1}$和一個pnp電晶體$Q_{2}$。如果npn電晶體$Q_{1}$的基極到發射極電壓為正且大於導通電壓，則它將導通。否則，它將截止。
pnp電晶體$Q_{2}$用作緩衝器，以隔離復位輸入與SR觸發器和npn電晶體$Q_{1}$。
555定時器IC的功能框圖中使用的反相器不僅執行反相操作，而且還放大功率電平。

555定時器IC可用於單穩態工作，以在輸出端產生脈衝。類似地，它可用於非穩態工作，以在輸出端產生方波。

鎖相環IC

鎖相環(PLL)是線性系統中至關重要的模組之一。它在通訊系統（如雷達、衛星、調頻等）中很有用。

本章詳細討論了PLL和IC 565的框圖。

PLL的框圖

鎖相環（PLL）主要由以下三個模組組成：

相位檢測器
有源低通濾波器
壓控振盪器（VCO）

PLL的框圖如下所示：

相位檢測器的輸出作為有源低通濾波器的輸入。類似地，有源低通濾波器的輸出作為VCO的輸入。

PLL的工作原理如下：

相位檢測器產生一個直流電壓，該電壓與頻率為$f_{in}$的輸入訊號和頻率為$f_{out}$的反饋（輸出）訊號之間的相位差成正比。
相位檢測器是一個乘法器，在其輸出端產生兩個頻率分量：頻率$f_{in}$和$f_{out}$的和以及頻率$f_{in}$和$f_{out}$的差。
有源低通濾波器在其輸出端產生一個直流電壓，在消除相位檢測器輸出端存在的高頻分量後。它還可以放大訊號。
VCO在沒有輸入施加到它時產生一個具有特定頻率的訊號。可以透過向其施加直流電壓將其頻率偏移到任一側。因此，頻率偏差與低通濾波器輸出端存在的直流電壓成正比。

上述操作持續進行，直到VCO頻率等於輸入訊號頻率。根據應用型別，我們可以使用有源低通濾波器的輸出或VCO的輸出。PLLs用於許多應用，例如調頻解調器、時鐘發生器等。

PLL以以下三種模式之一工作：

自由執行模式
捕獲模式
鎖定模式

最初，當沒有輸入施加到PLL時，PLL以自由執行模式工作。當向PLL施加具有某個頻率的輸入訊號時，VCO的輸出訊號頻率將開始變化。在此階段，據說PLL處於捕獲模式。VCO的輸出訊號頻率將持續變化，直到它等於輸入訊號頻率。現在，據說PLL處於鎖定模式。

IC 565

IC 565是最常用的鎖相環IC。它是一個14引腳雙列直插封裝（DIP）。IC 565的引腳圖如下所示：

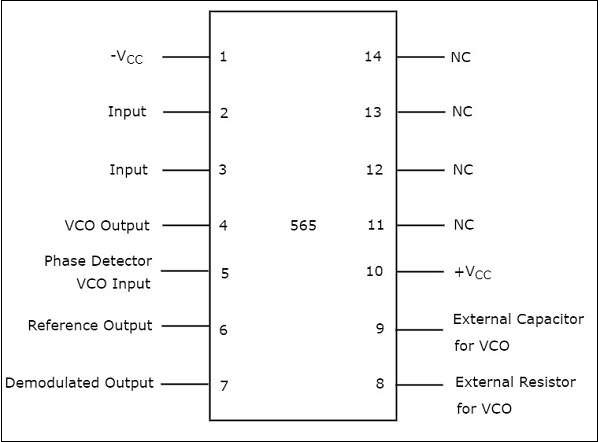
每個引腳的用途從上圖中不言而喻。在14個引腳中，只有10個引腳（引腳編號1到10）用於PLL的操作。因此，其餘4個引腳（引腳編號11到14）標記為NC（無連線）。

當引腳2和3接地時，VCO在IC 565的引腳4處產生輸出。在數學上，我們可以將VCO的輸出頻率$f_{out}$寫成。

$$f_{out}=\frac{0.25}{R_VC_V}$$

其中，

$R_{V}$是連線到引腳8的外部電阻

$C_{V}$是連線到引腳9的外部電容

透過選擇合適的$R_{V}$和$C_{V}$值，我們可以固定（確定）VCO的輸出頻率$f_{out}$。
引腳4和5需要用外部導線短路，以便將VCO的輸出作為相位檢測器的一個輸入。
IC 565具有$3.6K\Omega$的內部電阻。需要在引腳7和10之間連線一個電容C，以與該內部電阻形成低通濾波器。

請注意，根據要求，我們必須正確配置IC 565的引腳。

穩壓器

穩壓器的功能是無論輸入電壓波動和（或）負載電流變化如何，都能在輸出端保持恆定的直流電壓。換句話說，穩壓器產生一個穩定的直流輸出電壓。

穩壓器也以積體電路（IC）的形式提供。這些被稱為穩壓器IC。

穩壓器的型別

穩壓器有兩種型別：

固定穩壓器
可調穩壓器

本章將逐一討論這兩種型別的穩壓器。

固定穩壓器

固定穩壓器產生固定的直流輸出電壓，該電壓可以是正電壓或負電壓。換句話說，一些固定穩壓器產生正固定直流電壓值，而另一些則產生負固定直流電壓值。

78xx穩壓器IC產生正固定直流電壓值，而79xx穩壓器IC產生負固定直流電壓值。

使用78xx和79xx穩壓器IC時，需要注意以下幾點：

“xx”對應於一個兩位數字，表示穩壓器IC產生的電壓量（幅值）。
78xx和79xx穩壓器IC都各有3個引腳，第三個引腳用於從它們收集輸出。
這兩種IC的第一和第二個引腳的用途不同：
- 78xx穩壓器IC的第一和第二個引腳分別用於連線輸入和接地。
- 79xx穩壓器IC的第一和第二個引腳分別用於連線接地和輸入。

示例

7805穩壓器IC產生+5伏的直流電壓。
7905穩壓器IC產生-5伏的直流電壓。

下圖顯示瞭如何透過使用具有必要連線的正固定穩壓器在輸出端產生正固定電壓。

在上圖中，該圖顯示了一個正固定穩壓器，輸入電容C_i用於防止不需要的振盪，輸出電容C₀用作線路濾波器以改善瞬態響應。

注意：透過使用具有適當連線的負固定穩壓器，可以在輸出端獲得負固定電壓。

可調穩壓器

可調穩壓器產生直流輸出電壓，該電壓可以調整到某個電壓範圍內的任何其他值。因此，可調穩壓器也稱為可變穩壓器。

可調穩壓器的直流輸出電壓值可以是正電壓或負電壓。

LM317穩壓器IC

LM317穩壓器IC可用於產生所需的可用電壓範圍內的正固定直流電壓值。

LM317穩壓器IC有3個引腳。第一個引腳用於調節輸出電壓，第二個引腳用於收集輸出，第三個引腳用於連線輸入。

可調引腳（端子）配備了一個可變電阻，允許輸出在較寬的範圍內變化。

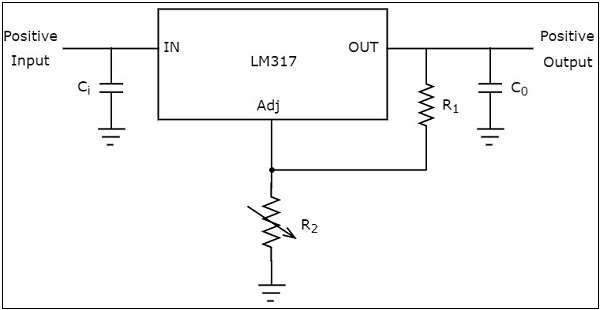
上圖顯示了一個非穩壓電源驅動一個常用的LM 317穩壓器IC。該IC可以在1.25 V至37 V的可調輸出範圍內提供1.5A的負載電流。

資料轉換器

所有現實世界的量都是模擬的。我們可以用模擬訊號來表示這些量。模擬訊號是一個隨時間變化的訊號，在給定的時間段內具有任意數量的值（變化）。

與此相反，數字訊號會突然從一個電平變到另一個電平，並且在給定的時間段內僅具有有限數量的值（變化）。

本章討論了資料轉換器的型別及其規格。

資料轉換器的型別

可以使用模擬訊號工作的電子電路稱為類比電路。類似地，可以使用數字訊號工作的電子電路稱為數位電路。資料轉換器是一種將一種形式的資料轉換為另一種形式的電子電路。

資料轉換器有兩種型別：

模數轉換器
數模轉換器

如果我們想將類比電路的輸出作為數位電路的輸入，則必須在它們之間放置一個介面電路。將模擬訊號轉換為數字訊號的此介面電路稱為模數轉換器。

類似地，如果我們想將數位電路的輸出作為類比電路的輸入，則必須在它們之間放置一個介面電路。將數字訊號轉換為模擬訊號的此介面電路稱為數模轉換器。

請注意，某些模數轉換器可能需要數模轉換器作為其操作的內部模組。

規格

以下是與資料轉換相關的規格：

解析度
轉換時間

解析度

解析度是模擬輸入電壓需要變化的最小量，才能在二進位制（數字）輸出中表示。它取決於數字輸出中使用的位數。

在數學上，解析度可以表示為

$$Resolution=\frac{1}{2^{N}}$$

其中，“N”是數字輸出中存在的位數。

從上述公式可以看出，解析度和位數之間存在反比關係。因此，隨著位數的增加，解析度降低，反之亦然。

解析度也可以定義為可以用二進位制表示的最大模擬輸入電壓與等效二進位制數之比。

在數學上，解析度可以表示為

$$Resolution=\frac{V_{FS}}{2^{N}-1}$$

其中，

$V_{FS}$是滿量程輸入電壓或最大模擬輸入電壓，

“N”是數字輸出中存在的位數。

轉換時間

資料轉換器將一種形式的資料（資訊）轉換為另一種形式的等效資料所需的時間稱為**轉換時間**。由於我們有兩種型別的資料轉換器，因此有兩種型別的轉換時間，如下所示

模數轉換時間
數模轉換時間

模數轉換器 (ADC) 將模擬輸入電壓轉換為其等效二進位制（數字）輸出所需的時間稱為**模數轉換時間**。它取決於數字輸出中使用的位數。

數模轉換器 (DAC) 將二進位制（數字）輸入轉換為其等效模擬輸出電壓所需的時間稱為**數模轉換時間**。它取決於二進位制（數字）輸入中存在的位數。

數模轉換器

**數模轉換器 (DAC)** 將數字輸入訊號轉換為模擬輸出訊號。數字訊號用二進位制程式碼表示，二進位制程式碼是 0 和 1 的組合。本章詳細介紹數模轉換器。

DAC 的**框圖**如下所示：

數模轉換器 (DAC) 由多個二進位制輸入和一個輸出組成。通常，DAC 的**二進位制輸入數**將是 2 的冪。

DAC 的型別

DAC 有**兩種型別**

加權電阻 DAC
R-2R 梯形 DAC

本節將詳細討論這兩種型別的 DAC：

加權電阻 DAC

加權電阻 DAC 透過在反相加法器電路中使用**二進位制加權電阻**產生一個與數字（二進位制）輸入幾乎相等的模擬輸出。簡而言之，二進位制加權電阻 DAC 稱為加權電阻 DAC。

3 位二進位制加權電阻 DAC 的**電路圖**如下所示：

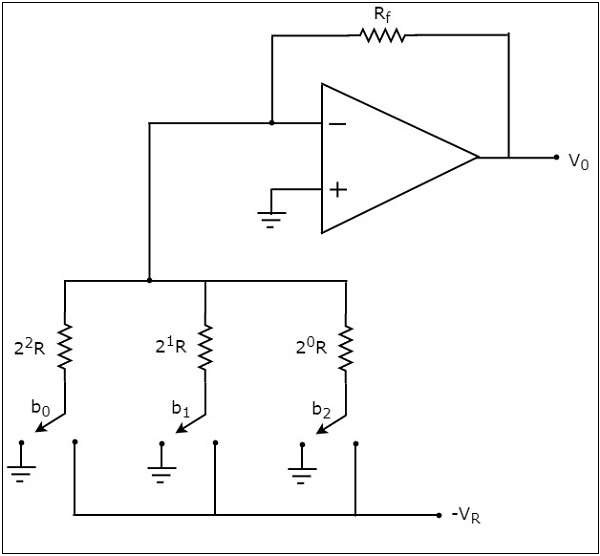
回想一下，二進位制數的位只能具有兩個值之一，即 0 或 1。假設**3 位二進位制輸入**為 $b_{2}b_{1}b_{0}$。這裡，位 $b_{2}$ 和 $b_{0}$ 分別表示**最高有效位 (MSB) 和最低有效位 (LSB)**。

上圖所示的**數字開關**將在相應的輸入位等於 '0' 時連線到地。類似地，上圖所示的數字開關將在相應的輸入位等於 '1' 時連線到負參考電壓 $-V_{R}$。

在上圖電路中，運算放大器的同相輸入端連線到地。這意味著在運算放大器的同相輸入端施加了 0 伏電壓。

根據**虛短概念**，運算放大器的反相輸入端的電壓與同相輸入端的電壓相同。因此，反相輸入端節點的電壓將為 0 伏。

反相輸入端節點的**節點方程**為

$$\frac{0+V_{R}b_{2}}{2^{0}R}+\frac{0+V_{R}b_{1}}{2^{1}R}+\frac{0+V_{R}b_{0}}{2^{2}R}+\frac{0-V_{0}}{R_{f}}=0$$

$$=>\frac{V_{0}}{R_{f}}=\frac{V_{R}b_{2}}{2^{0}R}+\frac{V_{R}b_{1}}{2^{1}R}+\frac{V_{R}b_{0}}{2^{2}R}$$

$$=>V_{0}=\frac{V_{R}R_{f}}{R}\left \{\frac{b_{2}}{2^{0}}+\frac{b_{1}}{2^{1}}+\frac{b_{0}}{2^{2}}\right \}$$

將 $R=2R_{f}$ 代入上述方程。

$$=>V_{0}=\frac{V_{R}R_{f}}{2R_{f}}\left \{\frac{b_{2}}{2^{0}}+\frac{b_{1}}{2^{1}}+\frac{b_{0}}{2^{2}}\right \}$$

$$=>V_{0}=\frac{V_{R}}{2}\left \{\frac{b_{2}}{2^{0}}+\frac{b_{1}}{2^{1}}+\frac{b_{0}}{2^{2}}\right \}$$

上述方程表示 3 位二進位制加權電阻 DAC 的**輸出電壓方程**。由於二進位制（數字）輸入中的位數為 3，因此對於固定的參考電壓 $V_{R}$，透過將二進位制輸入從 000 更改為 111，我們將得到 7 個可能的輸出電壓值。

我們可以根據 3 位二進位制加權電阻 DAC 的輸出電壓方程，寫出 N 位二進位制加權電阻 DAC 的**廣義輸出電壓方程**，如下所示。

$$=>V_{0}=\frac{V_{R}}{2}\left \{ \frac{b_{N-1}}{2^{0}}+ \frac{b_{N-2}}{2^{1}}+....+\frac{b_{0}}{2^{N-1}} \right \}$$

二進位制加權電阻 DAC 的**缺點**如下：

隨著數字輸入中存在的位數增加，對應於 LSB 和 MSB 的電阻值之間的差異也會增加。
隨著數字輸入中存在的位數增加，設計更精確的電阻變得困難。

R-2R 梯形 DAC

R-2R 梯形 DAC 克服了二進位制加權電阻 DAC 的缺點。顧名思義，R-2R 梯形 DAC 透過在反相加法器電路中使用**R-2R 梯形網路**產生一個與數字（二進位制）輸入幾乎相等的模擬輸出。

3 位 R-2R 梯形 DAC 的**電路圖**如下所示：

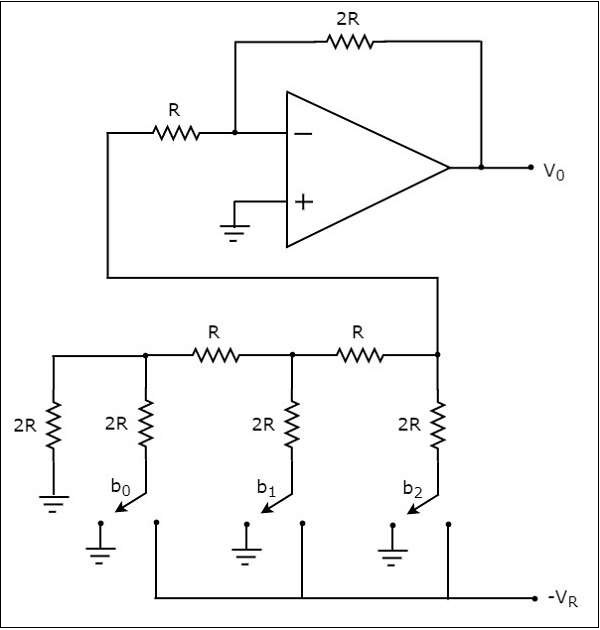
回想一下，二進位制數的位只能具有兩個值之一，即 0 或 1。假設**3 位二進位制輸入**為 $b_{2}b_{1}b_{0}$。這裡，位 $b_{2}$ 和 $b_{0}$ 分別表示最高有效位 (MSB) 和最低有效位 (LSB)。

上圖所示的數字開關將在相應的輸入位等於 '0' 時連線到地。類似地，上圖所示的數字開關將在相應的輸入位等於 '1' 時連線到負參考電壓 $-V_{R}$。

很難得到 R-2R 梯形 DAC 的廣義輸出電壓方程。但是，我們可以很容易地找到 R-2R 梯形 DAC 對於單個二進位制輸入組合的模擬輸出電壓值。

R-2R 梯形 DAC 的**優點**如下：

R-2R 梯形 DAC 僅包含兩個電阻值：R 和 2R。因此，選擇和設計更精確的電阻很容易。
如果數字輸入中存在更多位，則必須額外包含所需的 R-2R 部分。

由於上述優點，R-2R 梯形 DAC 比二進位制加權電阻 DAC 更受歡迎。

DAC示例問題

在上一章中，我們討論了兩種型別的 DAC。本章討論了一個基於 R-2R 梯形 DAC 的示例問題。

示例

讓我們找到當二進位制輸入 $b_{2}b_{1}b_{0}$ = 100 時，R-2R 梯形 DAC 的模擬輸出電壓值。

電路圖及其簡化

當二進位制輸入 $b_{2}b_{1}b_{0}$ = 100 應用於 3 位 R-2R 梯形 DAC 時，其**電路圖**如下所示：

在上圖電路中，相對於地，存在**A 點**左側電阻的串聯和並聯組合。因此，我們可以用一個電阻來代替整個電阻網路，該電阻的電阻值為 $2R\Omega$。

**簡化的電路圖**如下所示：

我們可以使用戴維南等效電路來替換連線到相對於地**B 點**左側的網路部分。**修改後的電路圖**如下所示：

在上圖電路中，存在兩個電阻的串聯組合。將此組合替換為單個電阻。簡化後的最終**電路圖**如下所示：

現在，上圖電路圖看起來像一個**反相放大器**。它具有 $-\frac{V_{R}}{2}$ 伏的輸入電壓、$2R\Omega$ 的輸入電阻和 $2R\Omega$ 的反饋電阻。

上圖所示電路的**輸出電壓**為：

$$V_{0}=-\frac{2R}{2R}\left(-\frac{V_{R}}{2}\right)$$

$$V_{0}=\frac{V_{R}}{2}$$

因此，對於二進位制輸入 $b_{2}b_{1}b_{0}$ = 100，3 位 R-2R 梯形 DAC 的**輸出電壓**為 $\frac{V_{R}}{2}$ 伏。

直達型ADC

模數轉換器 **(ADC)** 將模擬訊號轉換為數字訊號。數字訊號用二進位制程式碼表示，二進位制程式碼是 0 和 1 的組合。

ADC 的**框圖**如下所示：

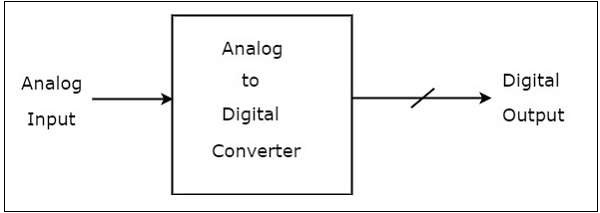
觀察上圖所示的圖，模數轉換器 **(ADC)** 由一個模擬輸入和多個二進位制輸出組成。通常，ADC 的二進位制輸出數將是 2 的冪。

ADC 有**兩種型別**：直接型 ADC 和間接型 ADC。本章詳細討論直接型 ADC。

如果 ADC 透過利用內部生成的等效數字（二進位制）程式碼與模擬輸入進行比較來直接執行模數轉換，則稱為**直接型 ADC**。

以下是直接型 ADC 的**示例**：

計數器型 ADC
逐次逼近型 ADC
閃速型 ADC

本節將詳細討論這些直接型 ADC。

計數器型 ADC

**計數器型 ADC** 透過在內部使用計數器操作產生一個近似等於模擬輸入的數字輸出。

計數器型 ADC 的**框圖**如下所示：

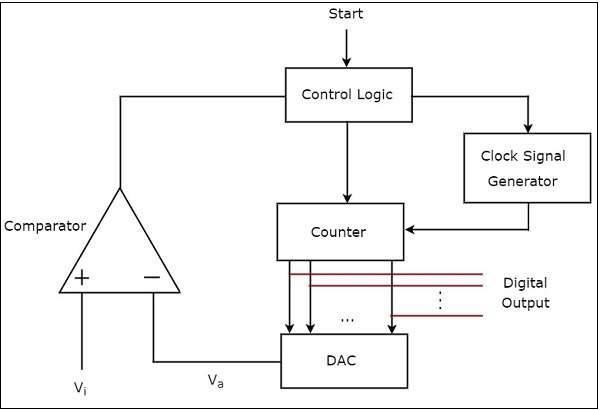
計數器型 ADC 主要由 5 個模組組成：時鐘訊號發生器、計數器、DAC、比較器和控制邏輯。

計數器型 ADC 的**工作原理**如下：

當**控制邏輯**收到啟動命令訊號時，它會重置計數器並使能時鐘訊號發生器，以便向計數器傳送時鐘脈衝。
**計數器**對於每個時鐘脈衝都會遞增 1，其值將為二進位制（數字）格式。計數器的此輸出用作 DAC 的輸入。
**DAC** 將接收到的二進位制（數字）輸入（即計數器的輸出）轉換為模擬輸出。比較器將此模擬值 $V_{a}$ 與外部模擬輸入值 $V_{i}$ 進行比較。
只要 𝑉𝑖 大於 $V_{a}$，**比較器的輸出**將為**'1'**。只要控制邏輯從比較器的輸出接收 '1'，上述兩步中提到的操作就會繼續。
當 $V_{i}$ 小於或等於 $V_{a}$ 時，**比較器的輸出**將為**'0'**。因此，控制邏輯從比較器的輸出接收 '0'。然後，控制邏輯停用時鐘訊號發生器，使其不會向計數器傳送任何時鐘脈衝。
此時，計數器的輸出將顯示為**數字輸出**。它幾乎等效於相應的外部模擬輸入值 $V_{i}$。

逐次逼近型 ADC

逐次逼近型ADC透過內部使用逐次逼近技術，產生一個與模擬輸入近似相等的數字輸出。

逐次逼近型ADC的框圖如下所示：

逐次逼近型ADC主要由5個模組組成：時鐘訊號發生器、逐次逼近暫存器（SAR）、DAC、比較器和控制邏輯。

工作原理如下：

當收到開始命令訊號時，控制邏輯會復位SAR的所有位，並使能時鐘訊號發生器，以便向SAR傳送時鐘脈衝。
基於比較器的輸出，SAR中的二進位制（數字）資料將在每個時鐘脈衝時更新。SAR的輸出作為DAC的輸入。
DAC將接收到的數字輸入（即SAR的輸出）轉換為模擬輸出。比較器將此模擬值$V_{a}$與外部模擬輸入值$V_{i}$進行比較。
只要$V_{i}$大於$V_{a}$，比較器的輸出將為‘1’。類似地，當$V_{i}$小於或等於$V_{a}$時，比較器的輸出將為‘0’。
上述步驟中提到的操作將持續進行，直到數字輸出有效。

當數字輸出幾乎等效於相應的外部模擬輸入值$V_{i}$時，它將是有效的。

閃速型 ADC

閃速型ADC能夠在瞬間為相應的模擬輸入產生一個等效的數字輸出。因此，閃速型ADC是最快的ADC。

3位閃速型ADC的電路圖如下所示：

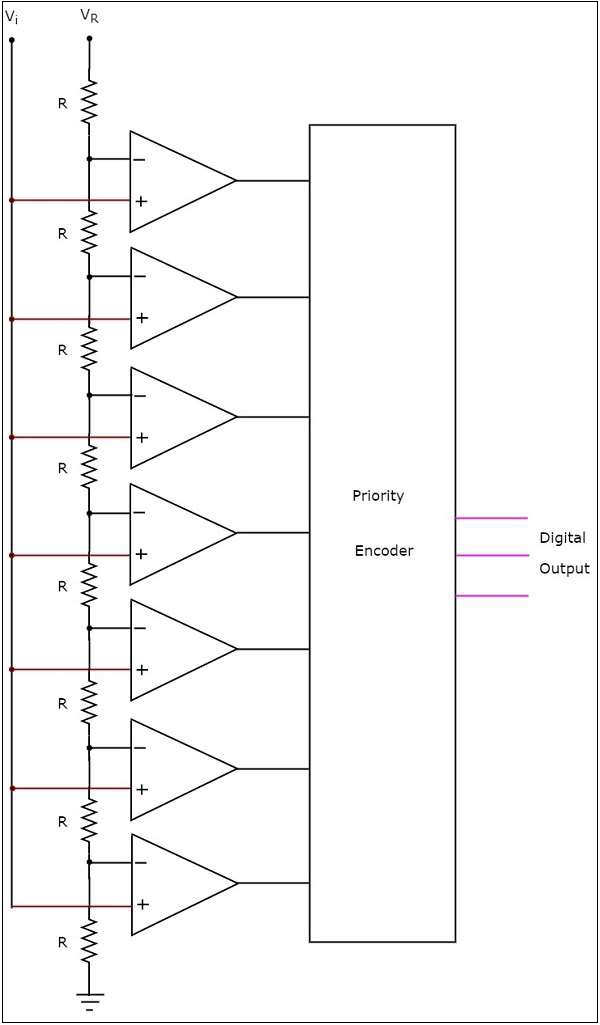
3位閃速型ADC由分壓網路、7個比較器和一個優先編碼器組成。

3位閃速型ADC的工作原理如下。

分壓網路包含8個等值的電阻。參考電壓$V_{R}$施加在整個網路上，相對於地。從下到上，每個電阻兩端的電壓降相對於地將是$\frac{V_{R}}{8}$的整數倍（從1到8）。
外部輸入電壓$V_{i}$施加到所有比較器的同相端。從下到上，每個電阻兩端的電壓降相對於地施加到從下到上的比較器的反相端。
在同一時刻，所有比較器將外部輸入電壓與各自另一輸入端存在的電壓降進行比較。這意味著，每個比較器並行地進行比較操作。
只要$V_{i}$大於各自另一輸入端存在的電壓降，比較器的輸出將為‘1’。類似地，當$V_{i}$小於或等於各自另一輸入端存在的電壓降時，比較器的輸出將為‘0’。
所有比較器的輸出都連線到優先編碼器的輸入。該優先編碼器產生一個二進位制程式碼（數字輸出），該程式碼對應於具有‘1’的最高優先順序輸入。
因此，優先編碼器的輸出就是外部模擬輸入電壓$V_{i}$的二進位制等效值（數字輸出）。

閃速型ADC用於需要將模擬輸入轉換為數字資料的速度非常快的應用場合。

間接型ADC

在上一章中，我們討論了什麼是ADC以及直接型ADC的示例。本章討論間接型ADC。

如果ADC透過間接方法執行模擬到數字轉換，則稱為間接型ADC。通常，它首先將模擬輸入轉換為時間的線性函式（或頻率），然後產生數字（二進位制）輸出。

雙積分ADC是間接型ADC的最佳示例。本章將詳細討論它。

雙積分ADC

顧名思義，雙積分ADC透過使用兩種（雙）斜率技術，為相應的模擬輸入產生一個等效的數字輸出。

雙積分ADC的框圖如下所示：

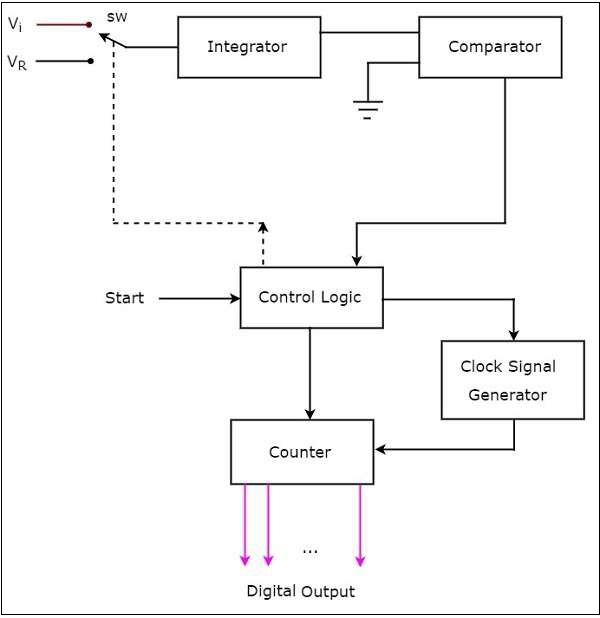
雙積分ADC主要由5個模組組成：積分器、比較器、時鐘訊號發生器、控制邏輯和計數器。

工作原理如下：

當收到開始命令訊號時，控制邏輯會復位計數器並使能時鐘訊號發生器，以便向計數器傳送時鐘脈衝。
當收到開始命令訊號時，控制邏輯將開關sw切換到連線到外部模擬輸入電壓$V_{i}$。此輸入電壓施加到積分器。
積分器的輸出連線到比較器的兩個輸入之一，比較器的另一個輸入連線到地。
比較器將積分器的輸出與零伏（地）進行比較，併產生一個輸出，該輸出被應用於控制邏輯。
計數器在每個時鐘脈衝時加1，其值將以二進位制（數字）格式表示。當它在達到最大計數值後加1時，它會向控制邏輯產生溢位訊號。此時，計數器所有位都將為零。
現在，控制邏輯將開關sw切換到連線到負參考電壓$-V_{ref}$。此負參考電壓施加到積分器。它去除儲存在電容中的電荷，直到其變為零。
此時，比較器的兩個輸入都為零伏。因此，比較器向控制邏輯傳送訊號。現在，控制邏輯停用時鐘訊號發生器並保持（儲存）計數器值。計數器值與外部模擬輸入電壓成正比。
此時，計數器的輸出將顯示為**數字輸出**。它幾乎等效於相應的外部模擬輸入值 $V_{i}$。

雙積分ADC用於將模擬輸入轉換為等效數字（二進位制）資料時，精度非常重要的應用場合。

列印頁面