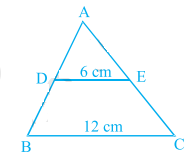
在下圖中，如果\( \mathrm{DE} \| \mathrm{BC} \)，求 ar (ADE) 和 ar (DECB) 的比值。
"

已知

\( \mathrm{DE} \| \mathrm{BC} \)

要求

我們必須找到 ar (ADE) 和 ar (DECB) 的比值。

解答

在△ABC 和△ADE 中，

∠ABC = ∠ADE (同位角)

∠ACB = ∠AED (同位角)

∠A = ∠A

因此，根據 AA 相似性，

△ABC ~ △AED

這意味著，

$\frac{\operatorname{ar}(\triangle A D E)}{\operatorname{ar}(\triangle A B C)}=(\frac{DE}{BC})^2$

$=\frac{(6)^{2}}{(12)^{2}}$

$=(\frac{1}{2})^{2}$

$=\frac{1}{4}$

設 ar (△ADE) = k

這意味著，

ar (△ABC) = 4k

ar (DECB) = ar(ABC) - ar(ADE)

= 4k - k

= 3k

因此，

ar(ADE) : ar(DECB) = k : 3k

$=1: 3$

ar (ADE) 和 ar (DECB) 的比值為 1:3。

Tutorialspoint

更新於：2022年10月10日

246 次瀏覽

開啟你的職業生涯

完成課程獲得認證

開始學習