數字通訊 - 線路編碼

---

---

線路編碼是在傳輸線上進行數字訊號資料傳輸時使用的程式碼。選擇此編碼過程是為了避免訊號重疊和失真，例如符號間干擾。

線路編碼的特性

以下是線路編碼的特性 -

• 由於編碼是為了在單個訊號上傳輸更多位元，因此使用的頻寬大大降低。

• 對於給定的頻寬，功率得到有效利用。

• 錯誤機率大大降低。

• 執行錯誤檢測，並且雙極性也具有校正功能。

• 功率密度更有利。

• 定時內容充足。

• 避免長串的1和0以保持透明度。

線路編碼的型別

線路編碼有 3 種類型

• 單極性
• 極性
• 雙極性

單極性訊號

單極性訊號也稱為開關鍵控或簡稱OOK。

脈衝的存在表示1，脈衝的不存在表示0。

單極性訊號有兩種變體 -

• 不歸零 (NRZ)
• 歸零 (RZ)

單極性不歸零 (NRZ)

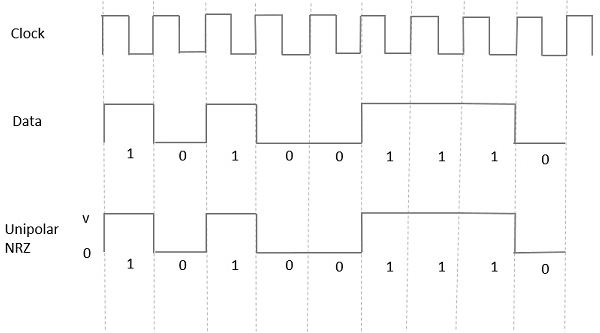
在這種型別的單極性訊號中，資料中的高電平由稱為標記的正脈衝表示，其持續時間T₀等於符號位元持續時間。資料輸入中的低電平沒有脈衝。

下圖清楚地描繪了這一點。

優點

單極性 NRZ 的優點是 -

• 它很簡單。
• 需要較少的頻寬。

缺點

單極性 NRZ 的缺點是 -

• 沒有執行錯誤校正。

• 低頻分量的存在可能會導致訊號下降。

• 沒有時鐘。

• 可能會發生同步丟失（尤其是在長串的1和0的情況下）。

單極性歸零 (RZ)

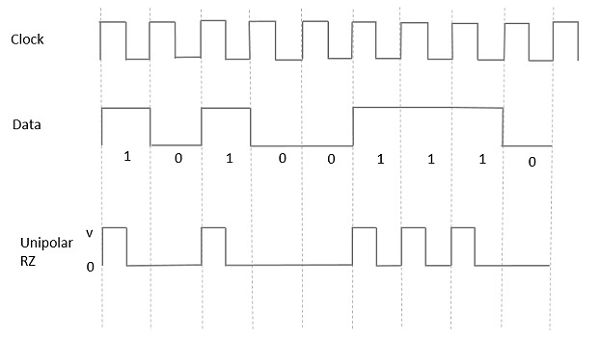
在這種型別的單極性訊號中，儘管資料中的高電平由標記脈衝表示，但其持續時間T₀小於符號位元持續時間。位元持續時間的一半保持高電平，但它立即返回到零，並在位元持續時間的剩餘一半顯示脈衝不存在。

藉助下圖可以清楚地理解這一點。

優點

單極性 RZ 的優點是 -

• 它很簡單。
• 位於符號速率處的譜線可用作時鐘。

缺點

單極性 RZ 的缺點是 -

• 沒有錯誤校正。
• 佔用單極性 NRZ 兩倍的頻寬。
• 在訊號在 0 Hz 處非零的地方會引起訊號下降。

極性訊號

極性訊號有兩種方法。他們是 -

• 極性 NRZ
• 極性 RZ

極性 NRZ

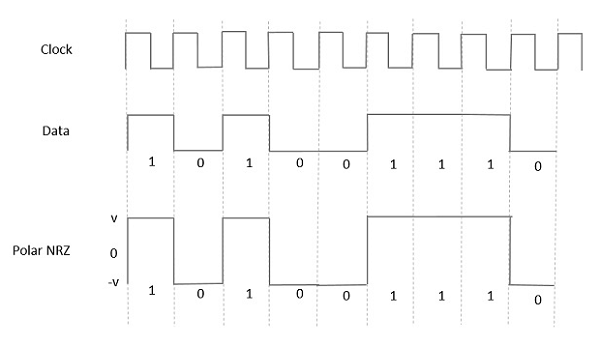
在這種型別的極性訊號中，資料中的高電平由正脈衝表示，而資料中的低電平由負脈衝表示。下圖很好地描繪了這一點。

優點

極性 NRZ 的優點是 -

• 它很簡單。
• 不存在低頻分量。

缺點

極性 NRZ 的缺點是 -

• 沒有錯誤校正。

• 沒有時鐘。

• 在訊號在0 Hz處非零的地方會引起訊號下降。

極性 RZ

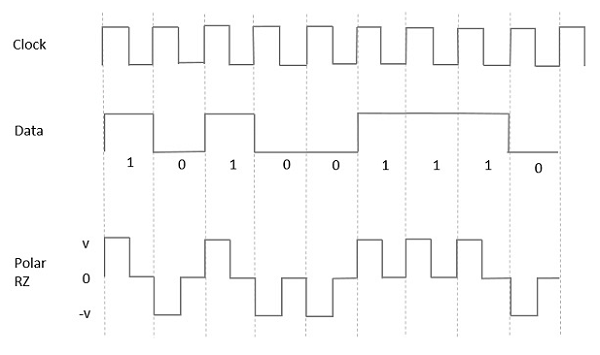
在這種型別的極性訊號中，儘管資料中的高電平由標記脈衝表示，但其持續時間T₀小於符號位元持續時間。位元持續時間的一半保持高電平，但它立即返回到零，並在位元持續時間的剩餘一半顯示脈衝不存在。

但是，對於低輸入，負脈衝表示資料，零電平在位元持續時間的另一半保持相同。下圖清楚地描繪了這一點。

優點

極性 RZ 的優點是 -

• 它很簡單。
• 不存在低頻分量。

缺點

極性 RZ 的缺點是 -

• 沒有錯誤校正。

• 沒有時鐘。

• 佔用極性 NRZ 兩倍的頻寬。

• 在訊號在0 Hz處非零的地方會引起訊號下降。

雙極性訊號

這是一種編碼技術，它具有三個電壓電平，即+、-和0。這種訊號稱為雙二進位制訊號。

這種型別的一個示例是交替標記反轉 (AMI)。對於1，電壓電平從 + 變換到 – 或從 – 變換到 +，交替的1具有相同的極性。0將具有零電壓電平。

即使在這種方法中，我們也有兩種型別。

• 雙極性 NRZ
• 雙極性 RZ

從迄今為止討論的模型中，我們瞭解了 NRZ 和 RZ 之間的區別。它在這裡也以同樣的方式進行。下圖清楚地描繪了這一點。

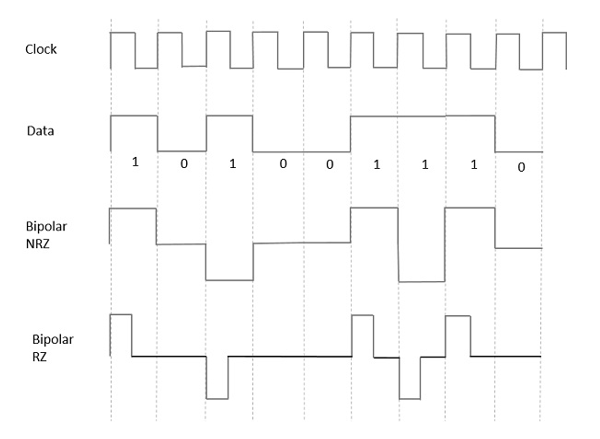
上圖同時顯示了雙極性 NRZ 和 RZ 波形。在 NRZ 型別中，脈衝持續時間和符號位元持續時間相等，而在 RZ 型別中，脈衝持續時間是符號位元持續時間的一半。

優點

以下是優點 -

• 它很簡單。

• 不存在低頻分量。

• 佔用比單極性和極性 NRZ 方案更低的頻寬。

• 此技術適用於透過交流耦合線路傳輸，因為這裡不會發生訊號下降。

• 它具有單錯誤檢測功能。

缺點

以下是缺點 -

• 沒有時鐘。
• 長串資料會導致同步丟失。

功率譜密度

描述訊號功率如何在頻域中分佈在各個頻率上的函式稱為功率譜密度 (PSD)。

PSD 是自相關（觀測值之間的相似性）的傅立葉變換。它採用矩形脈衝的形式。

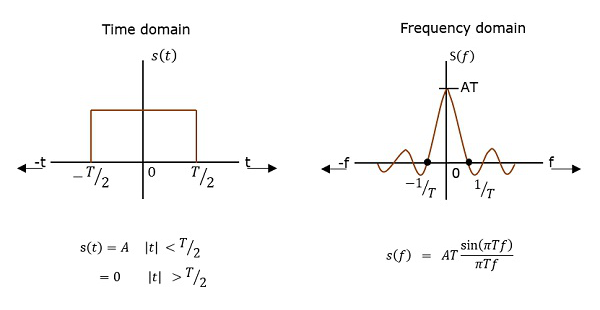
PSD 推導

根據愛因斯坦-維納-辛欽定理，如果知道隨機過程的自相關函式或功率譜密度，則可以精確地找到另一個。

因此，為了推匯出功率譜密度，我們將使用功率訊號 $x(t)$ 的時間自相關 $(R_x(\tau))$，如下所示。

$R_x(\tau) = \lim_{T_p \rightarrow \infty}\frac{1}{T_p}\int_{\frac{{-T_p}}{2}}^{\frac{T_p}{2}}x(t)x(t + \tau)dt$

由於 $x(t)$ 由脈衝組成，因此 $R_x(\tau)$ 可以寫成

$R_x(\tau) = \frac{1}{T}\displaystyle\sum\limits_{n = -\infty}^\infty R_n\delta(\tau - nT)$

其中 $R_n = \lim_{N \rightarrow \infty}\frac{1}{N}\sum_ka_ka_{k + n}$

瞭解到對於實訊號 $R_n = R_{-n}$，我們有

$S_x(w) = \frac{1}{T}(R_0 + 2\displaystyle\sum\limits_{n = 1}^\infty R_n \cos nwT)$

由於脈衝濾波器的頻譜為 $(w) \leftrightarrow f(t)$，我們有

$s_y(w) = \mid F(w) \mid^2S_x(w)$

$= \frac{\mid F(w) \mid^2}{T}(\displaystyle\sum\limits_{n = -\infty}^\infty R_ne^{-jnwT_{b}})$

$= \frac{\mid F(w) \mid^2}{T}(R_0 + 2\displaystyle\sum\limits_{n = 1}^\infty R_n \cos nwT)$

因此，我們得到了功率譜密度的方程。使用它，我們可以找到各種線路編碼的 PSD。