
數字通訊 - 差錯控制編碼
噪聲或錯誤是訊號中的主要問題,它會干擾通訊系統的可靠性。差錯控制編碼是用於控制錯誤發生的編碼過程。這些技術有助於錯誤檢測和錯誤糾正。
根據應用的數學原理,存在許多不同的糾錯碼。但是,歷史上,這些程式碼已被分為線性分組碼和卷積碼。
線性分組碼
線上性分組碼中,奇偶校驗位和訊息位具有線性組合,這意味著生成的碼字是任意兩個碼字的線性組合。
讓我們考慮一些資料塊,每個資料塊包含k位。這些位與每個資料塊包含n位的塊對映。這裡n大於k。傳送器新增冗餘位,即(n-k)位。比率k/n是位元速率。它用r表示,r的值為r < 1。
這裡新增的(n-k)位是奇偶校驗位。奇偶校驗位有助於錯誤檢測和錯誤糾正,以及定位資料。在傳輸的資料中,碼字的最左邊的位對應於訊息位,碼字的最右邊的位對應於奇偶校驗位。
系統碼
任何線性分組碼都可以是系統碼,直到它被改變。因此,未更改的分組碼稱為系統碼。
以下是根據其分配的碼字結構表示。
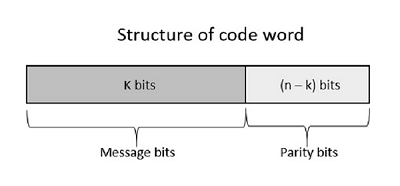
如果訊息沒有被改變,則稱為系統碼。這意味著資料的加密不應更改資料。
卷積碼
到目前為止,線上性碼中,我們已經討論了首選系統未更改的碼。在這裡,如果傳輸總共n位資料,則k位是訊息位,(n-k)位是奇偶校驗位。
在編碼過程中,奇偶校驗位從整個資料中減去,並且訊息位被編碼。現在,奇偶校驗位再次被新增,並且整個資料再次被編碼。
下圖給出了用於資訊傳輸的資料塊和資料流的示例。

上述整個過程是繁瑣的,存在缺點。當系統繁忙時,緩衝區的分配是一個主要問題。
卷積碼消除了此缺點。其中整個資料流被分配符號,然後傳輸。由於資料是位流,因此無需緩衝區進行儲存。
漢明碼
碼字的線性特性是兩個碼字的和也是一個碼字。漢明碼是一種線性糾錯碼,它可以檢測最多兩位錯誤,或者可以糾正一位錯誤而無需檢測未糾正的錯誤。
使用漢明碼時,使用額外的奇偶校驗位來識別單位元錯誤。要從一種位元模式轉換到另一種位元模式,需要更改資料中的少量位。此類位的數量可以稱為漢明距離。如果奇偶校驗的距離為 2,則可以檢測到一位翻轉。但這無法糾正。此外,任何兩位翻轉都無法檢測到。
然而,漢明碼比前面討論的錯誤檢測和糾正程式更好。
BCH 碼
BCH 碼以發明者Bose、Chaudari 和Hocquenghem 的名字命名。在 BCH 碼設計過程中,可以控制要糾正的符號數量,因此可以進行多位元糾正。BCH 碼是糾錯碼中的一種強大技術。
對於任何正整數m ≥ 3和t < 2m-1,都存在 BCH 二元碼。以下是此類程式碼的引數。
塊長度n = 2m-1
奇偶校驗位數n - k ≤ mt
最小距離dmin ≥ 2t + 1
此程式碼可以稱為t 錯糾正 BCH 碼。
迴圈碼
碼字的迴圈特性是碼字的任何迴圈移位也是一個碼字。迴圈碼遵循此迴圈特性。
對於線性碼C,如果每個碼字,即C = (C1, C2, ...... Cn)來自 C 的分量進行迴圈右移,則它成為一個碼字。此右移等於n-1次迴圈左移。因此,它在任何移位下都是不變的。因此,線性碼C,因為它在任何移位下都是不變的,可以稱為迴圈碼。
迴圈碼用於糾錯。它們主要用於糾正雙重錯誤和突發錯誤。
因此,這些是在接收器處要檢測的一些糾錯碼。這些程式碼可防止錯誤的引入並干擾通訊。它們還可以防止訊號被不需要的接收器竊聽。有一類信令技術可以實現這一點,這將在下一章中討論。