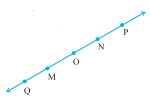
考慮如下線段 \( \overline{\mathrm{MN}} \) 的圖形。根據給定圖形，判斷下列語句的真假。
(a) \( \mathrm{Q}\)
解題步驟
我們需要判斷給定語句的真假。
解答
(a) 我們可以觀察到點 \( \mathrm{Q}, \mathrm{M}, \mathrm{O}, \mathrm{N}, \mathrm{P} \) 都線上段 \( \mathrm{MN} \) 上。
該語句為真。
(b) 我們可以觀察到 \( \mathrm{M}, \mathrm{O}, \mathrm{N} \) 是線段 \( \overline{\mathrm{MN}} \) 上的點。
該語句為真。
(c) 我們可以觀察到 \( \mathrm{M} \) 和 \( \mathrm{N} \) 是線段 \( \overline{\mathrm{MN}} \) 的端點。
該語句為真。
(d) 我們可以觀察到 \( \mathrm{O} \) 和 \( \mathrm{P} \) 是線段 \( \overline{\mathrm{OP}} \) 的端點。
該語句為假。
(e) 我們可以觀察到 \( M \) 不是線段 \( \overline{\mathrm{QO}} \) 的端點之一。
線段 \( \overline{\mathrm{QO}} \) 的端點是 Q 和 O。
該語句為假。
(f) 我們可以觀察到點 \( \mathrm{M} \) 不在射線 \( \overrightarrow{\mathrm{OP}} \) 上。
該語句為假。
(g) 射線 \( \overrightarrow{\mathrm{OP}} \) 的起點是點 O
射線 \( \overrightarrow{\mathrm{QP}} \) 的起點是點 Q
該語句為真。
(h) 射線 \( \overrightarrow{\mathrm{OP}} \) 的起點是點 O
射線 \( \overrightarrow{\mathrm{OM}} \) 的起點是點 O，但方向與上述射線相反。
該語句為假。
(i) 射線 \( \overrightarrow{\mathrm{OP}} \) 的起點是點 O
射線 \( \overrightarrow{\mathrm{OM}} \) 的起點是點 O，但方向與上述射線相反。
該語句為假。
(j) 我們可以觀察到 \( \mathrm{O} \) 是 \( \overrightarrow{\mathrm{OP}} \) 的起點。
該語句為假。
(k) 我們可以觀察到 \( \mathrm{N} \) 是 \( \overrightarrow{\mathrm{NP}} \) 的起點，\( \mathrm{N} \) 也是 \( \overrightarrow{\mathrm{NM}} \) 的起點。
該語句為真。
- 相關文章
- 判斷下列語句的真假。並說明理由。點 \( \mathrm{A}(4,3), \mathrm{B}(6,4), \mathrm{C}(5,-6) \) 和 \( \mathrm{D}(-3,5) \) 是平行四邊形的頂點。
- 判斷下列語句的真假。並說明理由。點 \( \mathrm{A}(3,1), \mathrm{B}(12,-2) \) 和 \( \mathrm{C}(0,2) \) 不能構成三角形的頂點。
- 判斷下列語句的真假。並說明理由。點 \( \mathrm{A}(2,7) \) 位於連線點 \( P(6,5) \) 和 \( Q(0,-4) \) 的線段的垂直平分線上。
- 判斷下列語句的真假：π 是一個無理數。
- 畫一個草圖，並在下列每種情況下進行適當的標記：(a) 點 \( P \) 線上段 \( \overline{\mathrm{AB}} \) 上。(b) \( \overline{\mathrm{XY}} \) 和 \( \overline{\mathrm{PQ}} \) 相交於點 \( \mathrm{M} \)。(c) 直線 \( l \) 包含 \( \bar{E} \) 和 \( \bar{F} \)，但不包含 \( \bar{D} \)。(d) \( \overline{\mathrm{OP}} \) 和 \( \overline{\mathrm{OQ}} \) 相交於點 \( O \)。
- 如果 \( \mathrm{B} \) 是 \( \overline{\mathrm{AC}} \) 的中點，\( \mathrm{C} \) 是 \( \overline{\mathrm{BD}} \) 的中點，其中 \( \mathrm{A}, \mathrm{B}, \mathrm{C}, \mathrm{D} \) 在一條直線上，為什麼 \( \mathrm{AB}=\mathrm{CD} \)？
- 指出下列哪些是三角形。\( \overline{AB}=7 \mathrm{~cm}, \overline{BC}=8 \mathrm{~cm}, \quad \overline{AC}=7 \mathrm{~cm} \)
- 判斷下列語句的真假。並說明理由。頂點為 \( \mathrm{A}(-2,0), \mathrm{B}(2,0) \) 和 \( \mathrm{C}(0,2) \) 的 \( \triangle \mathrm{ABC} \) 與頂點為 \( D(-4,0) E(4,0) \) 和 \( F(0,4) \) 的 \( \triangle \mathrm{DEF} \) 相似。
- 設 \( \overline{\mathrm{PQ}} \) 垂直於線段 \( \overline{\mathrm{XY}} \)。設 \( \overline{\mathrm{PQ}} \) 和 \( \overline{\mathrm{XY}} \) 相交於點 \( \mathrm{A} \)。\( \angle \mathrm{PAY} \) 的度數是多少？
- 給定一條線段 \( \overline{\mathrm{AB}} \)（長度未知），構造 \( \overline{\mathrm{PQ}} \)，使得 \( \overline{\mathrm{PQ}} \) 的長度是 \( \overline{\mathrm{AB}} \) 的兩倍。
- 判斷下列語句的真假。並說明理由。一個圓的圓心在原點，點 \( P(5,0) \) 在圓上。點 \( \mathrm{Q}(6,8) \) 在圓外。
- 已知 \( \overline{\mathrm{AB}} \) 長度為 \( 7.3 \mathrm{~cm} \)，\( \overline{\mathrm{CD}} \) 長度為 \( 3.4 \mathrm{~cm} \)，構造一條線段 \( \overline{XY} \)，使得 \( \overline{XY} \) 的長度等於 \( \overline{\mathrm{AB}} \) 和 \( \overline{\mathrm{CD}} \) 長度的差。透過測量進行驗證。
- 畫一條線段 \( \overline{\mathrm{PQ}} \)。不用測量 \( \overline{\mathrm{PQ}} \)，構造 \( \overline{\mathrm{PQ}} \) 的副本。
- 判斷下列語句的真假。並說明理由。每個二次方程恰好有一個根。
- 已知 \( \overline{\mathrm{AB}} \) 長度為 \( 3.9 \mathrm{~cm} \)，構造 \( \overline{\mathrm{PQ}} \)，使得 \( \overline{\mathrm{PQ}} \) 的長度是 \( \overline{\mathrm{AB}} \) 的兩倍。透過測量進行驗證。（提示：構造 \( \overline{\mathrm{PX}} \)，使得 \( \overline{\mathrm{PX}} \) 的長度等於 \( \overline{\mathrm{AB}} \) 的長度；然後擷取 \( \overline{\mathrm{XQ}} \)，使得 \( \overline{\mathrm{XQ}} \) 的長度也等於 \( \overline{\mathrm{AB}} \) 的長度。）
資料結構
網路
關係資料庫管理系統 (RDBMS)
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C語言程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理學
化學
生物學
數學
英語
經濟學
心理學
社會學
時尚研究
法學研究