• Compiler Design Video Tutorials

編譯器設計 - 語法分析

上一頁
下一頁

語法分析或解析是編譯器的第二階段。本章我們將學習構建解析器中使用的基本概念。

我們已經看到，詞法分析器可以藉助正則表示式和模式規則來識別標記。但是，由於正則表示式的侷限性，詞法分析器無法檢查給定句子的語法。正則表示式無法檢查平衡標記，例如括號。因此，此階段使用上下文無關文法 (CFG)，它由下推自動機識別。

另一方面，CFG 是正則文法的超集，如下圖所示

Relation of CFG and Regular Grammar

這意味著每個正則文法也是上下文無關的，但存在一些問題超出了正則文法的範圍。CFG 是描述程式語言語法的有用工具。

上下文無關文法

在本節中，我們將首先了解上下文無關文法的定義，並介紹在解析技術中使用的術語。

上下文無關文法有四個組成部分

  • 一組非終結符 (V)。非終結符是表示字串集的語法變數。非終結符定義有助於定義由文法生成的語言的字串集。

  • 一組標記，稱為終結符 (Σ)。終結符是從中形成字串的基本符號。

  • 一組產生式 (P)。文法的產生式指定了如何組合終結符和非終結符以形成字串。每個產生式由一個稱為產生式左邊的非終結符、一個箭頭和一個標記和/或非終結符序列組成，稱為產生式的右邊。

  • 其中一個非終結符被指定為起始符號 (S)；從這裡開始產生式。

透過重複用該非終結符的產生式右邊替換一個非終結符（最初是起始符號），從起始符號匯出字串。

示例

我們以迴文語言問題為例，它無法用正則表示式來描述。也就是說，L = { w | w = wR } 不是正則語言。但它可以用 CFG 來描述，如下所示

G = ( V, Σ, P, S )

其中

V = { Q, Z, N }
Σ = { 0, 1 }
P = { Q → Z | Q → N | Q → ℇ | Z → 0Q0 | N → 1Q1 }
S = { Q }

此文法描述了迴文語言，例如：1001、11100111、00100、1010101、11111 等。

語法分析器

語法分析器或解析器以標記流的形式接收來自詞法分析器的輸入。解析器根據產生式規則分析原始碼（標記流），以檢測程式碼中的任何錯誤。此階段的輸出是語法樹。

Syntax Analyzer

這樣，解析器完成了兩個任務，即解析程式碼，查詢錯誤並生成語法樹作為該階段的輸出。

即使程式中存在一些錯誤，也希望解析器解析整個程式碼。解析器使用錯誤恢復策略，我們將在本章後面學習。

推導

推導基本上是一系列產生式規則，用於獲取輸入字串。在解析過程中，我們對輸入的一些句子式進行兩個決定

  • 決定要替換哪個非終結符。
  • 決定用哪個產生式規則來替換非終結符。

為了決定用哪個產生式規則替換哪個非終結符，我們可以有兩個選擇。

最左推導

如果從左到右掃描和替換輸入的句子式，則稱為最左推導。透過最左推導匯出的句子式稱為左句子式。

最右推導

如果我們從右到左用產生式規則掃描和替換輸入，則稱為最右推導。從最右推導匯出的句子式稱為右句子式。

示例

產生式規則

E → E + E
E → E * E
E → id

輸入字串：id + id * id

最左推導是

E → E * E
E → E + E * E
E → id + E * E
E → id + id * E
E → id + id * id

請注意，總是首先處理最左邊非終結符。

最右推導是

E → E + E
E → E + E * E
E → E + E * id
E → E + id * id
E → id + id * id

語法樹

語法樹是推導的圖形描述。方便檢視如何從起始符號匯出字串。推導的起始符號成為語法樹的根。讓我們透過上一個主題中的一個示例來看一下。

我們採用 a + b * c 的最左推導

最左推導是

E → E * E
E → E + E * E
E → id + E * E
E → id + id * E
E → id + id * id

步驟 1

E → E * EParse Tree Construction

步驟 2

E → E + E * EParse Tree Construction

步驟 3

E → id + E * EParse Tree Construction

步驟 4

E → id + id * E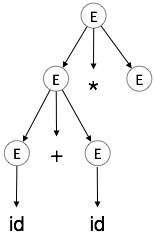Parse Tree Construction

步驟 5

E → id + id * id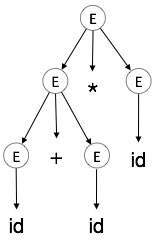Parse Tree Construction

在語法樹中

  • 所有葉子節點都是終結符。
  • 所有內部節點都是非終結符。
  • 中序遍歷給出原始輸入字串。

語法樹描述了運算子的結合性和優先順序。最深的子樹首先被遍歷，因此該子樹中的運算子優先於父節點中的運算子。

二義性

如果文法 G 對至少一個字串具有多個語法樹（左推導或右推導），則稱該文法為二義性的。

示例

E → E + E
E → E – E
E → id

對於字串 id + id – id，上述文法生成兩棵語法樹

Parse Tree Construction

由二義性文法生成的語言被稱為固有二義性。文法中的二義性對於編譯器構造不利。沒有方法可以自動檢測和消除二義性，但可以透過重寫整個文法而不含二義性，或者透過設定和遵循結合性和優先順序約束來消除二義性。

結合性

如果一個運算元兩側都有運算子，則運算子獲取此運算元的哪一側由這些運算子的結合性決定。如果運算為左結合性，則運算元將被左運算子獲取；如果運算為右結合性，則右運算子將獲取運算元。

示例

加法、乘法、減法和除法等運算子是左結合的。如果表示式包含

id op id op id

它將被計算為

(id op id) op id

例如，(id + id) + id

指數運算等運算子是右結合的，即同一表示式中的計算順序將為

id op (id op id)

例如，id ^ (id ^ id)

優先順序

如果兩個不同的運算子共享一個共同的運算元，則運算子的優先順序決定哪個運算子將獲取運算元。也就是說，2+3*4 可以有兩個不同的語法樹，一個對應於 (2+3)*4，另一個對應於 2+(3*4)。透過設定運算子之間的優先順序，可以很容易地解決這個問題。在前面的示例中，數學上 *（乘法）優先於 +（加法），因此表示式 2+3*4 將始終解釋為

2 + (3 * 4)

這些方法降低了語言或其文法中出現二義性的可能性。

左遞迴

如果文法有任何非終結符“A”，其推導包含“A”本身作為最左邊的符號，則該文法成為左遞迴。左遞迴文法被認為是自頂向下解析器的一個問題情況。自頂向下解析器從起始符號開始解析，起始符號本身是非終結符。因此，當解析器在其推導中遇到相同的非終結符時，它很難判斷何時停止解析左非終結符，並且它會進入無限迴圈。

示例

(1) A => Aα | β

(2) S => Aα | β 
    A => Sd

(1) 是直接左遞迴的示例，其中 A 是任何非終結符，α 表示非終結符的字串。

(2) 是間接左遞迴的示例。

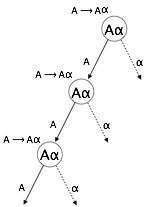
Left Recursion

自頂向下解析器將首先解析 A，這反過來將產生包含 A 本身的字串，並且解析器可能會永遠迴圈。

消除左遞迴

消除左遞迴的一種方法是使用以下技術

產生式

A => Aα | β

轉換為以下產生式

A => βA'
A'=> αA' | ε

這不會影響從文法匯出的字串，但它消除了直接左遞迴。

第二種方法是使用以下演算法，該演算法應消除所有直接和間接左遞迴。

START

Arrange non-terminals in some order like A1, A2, A3,…, An

   for each i from 1 to n
      {
      for each j from 1 to i-1
         {
         replace each production of form Ai ⟹Aj𝜸
         with Ai ⟹ δ1𝜸  | δ2𝜸 | δ3𝜸 |…| 𝜸 
         where Aj ⟹ δ1 | δ2|…| δn  are current Aj productions
         }
      }
   eliminate immediate left-recursion
   
END

示例

產生式集

S => Aα | β 
A => Sd

應用上述演算法後，應該變成

S => Aα | β 
A => Aαd | βd

然後，使用第一種技術消除直接左遞迴。

A  => βdA'
A' => αdA' | ε

現在沒有產生式具有直接或間接左遞迴。

左因子化

如果多個文法產生式規則具有共同的字首字串，則自頂向下解析器無法選擇應該使用哪個產生式來解析手中的字串。

示例

如果自頂向下解析器遇到類似這樣的產生式

A ⟹ αβ | α𝜸 | …

那麼它無法確定要遵循哪個產生式來解析字串，因為這兩個產生式都是從相同的終結符（或非終結符）開始的。為了消除這種混淆，我們使用一種稱為左因子化的技術。

左因子化轉換文法使其對自頂向下解析器有用。在這種技術中，我們為每個公共字首建立一個產生式，其餘的推導由新的產生式新增。

示例

上述產生式可以寫成

A => αA'
A'=> β | 𝜸 | …

現在解析器每個字首只有一個產生式，這使得決策更容易。

FIRST 集和 FOLLOW 集

解析表構造的重要部分是建立 FIRST 集和 FOLLOW 集。這些集合可以提供推導中任何終結符的實際位置。這是為了建立解析表，其中決定用某個產生式規則替換 T[A, t] = α。

FIRST 集

此集合用於確定非終結符在首位推匯出的終結符是什麼。例如：

α → t β

α在首位推匯出t（終結符）。因此，t ∈ FIRST(α)。

計算First集合的演算法

檢視FIRST(α)集合的定義

  • 如果α是終結符，則FIRST(α) = { α }。
  • 如果α是非終結符且α → ℇ是一個產生式，則FIRST(α) = { ℇ }。
  • 如果α是非終結符且α → 𝜸1 𝜸2 𝜸3 … 𝜸n，並且任何FIRST(𝜸)包含t，則t在FIRST(α)中。

First集合可以看作

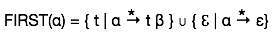
Follow集合

同樣地，我們計算在產生式規則中緊跟非終結符α之後的終結符是什麼。我們不考慮非終結符可以生成什麼，而是檢視緊跟非終結符產生式之後的下一個終結符是什麼。

計算Follow集合的演算法

  • 如果α是開始符號，則FOLLOW(α) = $

  • 如果α是非終結符，並且有產生式α → AB，則FIRST(B)（除了ℇ）在FOLLOW(A)中。

  • 如果α是非終結符，並且有產生式α → AB，其中B≠ℇ，則FOLLOW(A)在FOLLOW(α)中。

Follow集合可以看作：FOLLOW(α) = { t | S *αt*}

語法分析器的侷限性

語法分析器以標記的形式從詞法分析器接收輸入。詞法分析器負責語法分析器提供的標記的有效性。語法分析器有以下缺點：

  • 它無法確定標記是否有效；
  • 它無法確定標記是否在使用前已宣告；
  • 它無法確定標記是否在使用前已初始化；
  • 它無法確定對標記型別執行的操作是否有效。

這些任務由語義分析器完成，我們將在語義分析中學習。

列印頁面
上一頁
下一頁
廣告