編譯器設計 - 快速指南

編譯器設計 - 概述

計算機是軟體和硬體的平衡組合。硬體只是一塊機械裝置，其功能由相容的軟體控制。硬體以電子電荷的形式理解指令，這對應於軟體程式設計中的二進位制語言。二進位制語言只有兩個字母，0 和 1。為了發出指令，硬體程式碼必須以二進位制格式編寫，這僅僅是一系列的 1 和 0。對於計算機程式設計師來說，編寫這樣的程式碼將是一項困難且繁瑣的任務，這就是我們擁有編譯器來編寫此類程式碼的原因。

語言處理系統

我們已經瞭解到任何計算機系統都是由硬體和軟體組成的。硬體理解一種人類無法理解的語言。因此，我們用高階語言編寫程式，這更容易讓我們理解和記憶。然後，這些程式被輸入到一系列工具和作業系統元件中，以獲得機器可以使用的所需程式碼。這被稱為語言處理系統。

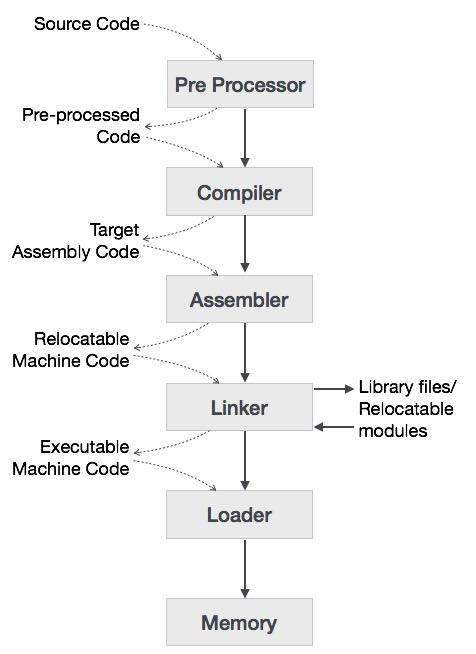
高階語言在各個階段轉換為二進位制語言。**編譯器**是一個將高階語言轉換為組合語言的程式。類似地，**彙編器**是一個將組合語言轉換為機器級語言的程式。

讓我們首先了解一下使用 C 編譯器在主機上如何執行程式。

使用者用 C 語言（高階語言）編寫程式。
C 編譯器編譯程式並將其轉換為彙編程式（低階語言）。
然後，彙編器將彙編程式轉換為機器程式碼（目標檔案）。
連結器工具用於將程式的所有部分連結在一起以執行（可執行機器程式碼）。
載入器將它們全部載入到記憶體中，然後執行程式。

在直接深入編譯器的概念之前，我們應該瞭解一些其他與編譯器緊密相關的工具。

預處理器

預處理器通常被認為是編譯器的一部分，它是一個為編譯器生成輸入的工具。它處理宏處理、增強、檔案包含、語言擴充套件等。

直譯器

直譯器與編譯器類似，將高階語言轉換為低階機器語言。它們之間的區別在於讀取原始碼或輸入的方式。編譯器一次讀取整個原始碼，建立標記，檢查語義，生成中間程式碼，執行整個程式，並且可能涉及多個遍。相反，直譯器從輸入中讀取一個語句，將其轉換為中間程式碼，執行它，然後依次獲取下一個語句。如果發生錯誤，直譯器將停止執行並報告它。而編譯器即使遇到多個錯誤也會讀取整個程式。

彙編器

彙編器將組合語言程式轉換為機器程式碼。彙編器的輸出稱為目標檔案，其中包含機器指令的組合以及將這些指令放置在記憶體中所需的資料。

連結器

連結器是一個計算機程式，它將各種目標檔案連結和合並在一起以生成可執行檔案。所有這些檔案可能都由單獨的彙編器編譯。連結器的主要任務是在程式中搜索和定位引用的模組/例程，並確定載入這些程式碼的記憶體位置，使程式指令具有絕對引用。

載入器

載入器是作業系統的一部分，負責將可執行檔案載入到記憶體中並執行它們。它計算程式的大小（指令和資料）併為其建立記憶體空間。它初始化各種暫存器以啟動執行。

交叉編譯器

在平臺 (A) 上執行並能夠為平臺 (B) 生成可執行程式碼的編譯器稱為交叉編譯器。

源到源編譯器

一個編譯器，它獲取一種程式語言的原始碼並將其轉換為另一種程式語言的原始碼，稱為源到源編譯器。

編譯器架構

根據編譯方式，編譯器可以大致分為兩個階段。

分析階段

稱為編譯器的前端，編譯器的**分析**階段讀取源程式，將其劃分為核心部分，然後檢查詞法、語法和語義錯誤。分析階段生成源程式的中間表示和符號表，這些都應作為輸入提供給綜合階段。

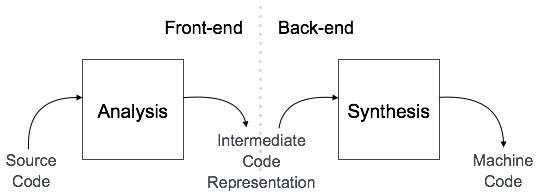
Analysis and Synthesis phase of compiler

綜合階段

稱為編譯器的後端，**綜合**階段在中間源程式碼表示和符號表的幫助下生成目標程式。

編譯器可以有多個階段和遍。

**遍**：遍是指編譯器遍歷整個程式。
**階段**：編譯器的階段是一個可區分的階段，它接收來自前一階段的輸入，進行處理併產生可以作為下一階段輸入的輸出。一個遍可以有多個階段。

編譯器的階段

編譯過程是一系列不同階段的序列。每個階段都接收來自其前一階段的輸入，有其自己的源程式表示，並將輸出提供給編譯器的下一階段。讓我們瞭解一下編譯器的階段。

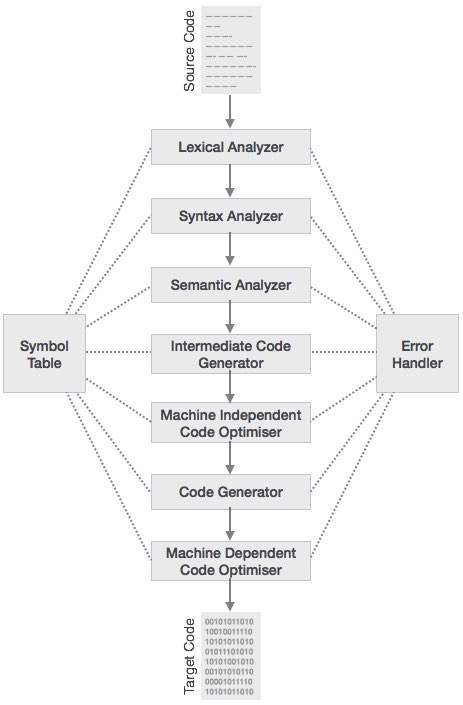
詞法分析

掃描程式的第一階段充當文字掃描程式。此階段掃描原始碼作為字元流，並將其轉換為有意義的詞素。詞法分析器以標記的形式表示這些詞素，例如

<token-name, attribute-value>

語法分析

下一階段稱為語法分析或**解析**。它以詞法分析生成的標記作為輸入，並生成語法樹（或語法樹）。在此階段，標記排列根據原始碼語法進行檢查，即解析器檢查標記構成的表示式在語法上是否正確。

語義分析

語義分析檢查構建的語法樹是否遵循語言規則。例如，值的賦值是在相容的資料型別之間，以及將字串新增到整數。此外，語義分析器跟蹤識別符號、其型別和表示式；識別符號是否在使用前宣告等。語義分析器產生帶註釋的語法樹作為輸出。

中間程式碼生成

語義分析後，編譯器為目標機器生成原始碼的中間程式碼。它表示某個抽象機的程式。它位於高階語言和機器語言之間。應以易於轉換為目標機器程式碼的方式生成此中間程式碼。

程式碼最佳化

下一階段對中間程式碼進行程式碼最佳化。最佳化可以理解為去除不必要的程式碼行，並安排語句的順序以加快程式執行速度，而不會浪費資源（CPU、記憶體）。

程式碼生成

在此階段，程式碼生成器獲取中間程式碼的最佳化表示，並將其對映到目標機器語言。程式碼生成器將中間程式碼轉換為（通常）可重定位機器程式碼的序列。機器程式碼指令序列執行與中間程式碼相同的任務。

符號表

它是在編譯器的所有階段都維護的一種資料結構。所有識別符號名稱及其型別都儲存在此處。符號表使編譯器能夠更輕鬆地快速搜尋識別符號記錄並檢索它。符號表也用於作用域管理。

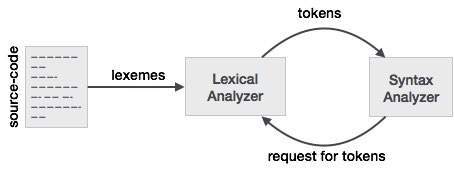
編譯器設計 - 詞法分析

詞法分析是編譯器的第一個階段。它接收來自以句子形式編寫的語言預處理器的修改後的原始碼。詞法分析器透過刪除原始碼中的任何空格或註釋，將這些語法分解成一系列標記。

如果詞法分析器發現標記無效，它會生成錯誤。詞法分析器與語法分析器緊密配合。它從原始碼讀取字元流，檢查合法標記，並在語法分析器需要時將資料傳遞給它。

標記

詞素被稱為標記中字元（字母數字）的序列。每個詞素被識別為有效標記都有一些預定義的規則。這些規則由語法規則透過模式定義。模式解釋了什麼可以是標記，這些模式透過正則表示式定義。

在程式語言中，關鍵字、常量、識別符號、字串、數字、運算子和標點符號可以被視為標記。

例如，在 C 語言中，變數宣告行

int value = 100;

包含標記

int (keyword), value (identifier), = (operator), 100 (constant) and ; (symbol).

標記規範

讓我們瞭解一下語言理論如何處理以下術語

字母表

任何有限的符號集 {0,1} 都是一組二進位制字母表，{0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F} 是一組十六進位制字母表，{a-z, A-Z} 是一組英語字母表。

字串

任何有限的字母（字元）序列稱為字串。字串的長度是字母出現的總數，例如，字串 tutorialspoint 的長度為 14，表示為 |tutorialspoint| = 14。沒有字母的字串，即長度為零的字串稱為空字串，表示為 ε（epsilon）。

特殊符號

一個典型的高階語言包含以下符號：

算術符號	加法(+)、減法(-)、模數(%)、乘法(*)、除法(/)
標點符號	逗號(,)、分號(;)、點(.)、箭頭(->)
賦值	=
特殊賦值	+=, /=, *=, -=
比較	==, !=, <, <=, >, >=
預處理器	#
位置說明符	&
邏輯	&, &&, \|, \|\|, !
移位運算子	>>, >>>, <<, <<<

語言

語言被認為是某些有限字母集上字串的有限集。計算機語言被認為是有限集，並且可以在它們上執行數學集運算。有限語言可以透過正則表示式來描述。

正則表示式

詞法分析器只需要掃描和識別屬於手頭語言的有限集的有效字串/標記/詞素。它搜尋語言規則定義的模式。

正則表示式能夠透過為有限符號字串定義模式來表達有限語言。由正則表示式定義的語法稱為**正則語法**。由正則語法定義的語言稱為**正則語言**。

正則表示式是指定模式的重要表示法。每個模式匹配一組字串，因此正則表示式充當一組字串的名稱。程式語言的標記可以用正則語言來描述。正則表示式的規範是一個遞迴定義的例子。正則語言易於理解並且具有高效的實現。

正則表示式遵循許多代數定律，這些定律可用於將正則表示式操作成等價的形式。

運算

語言的各種運算有

兩個語言 L 和 M 的並集寫成

L U M = {s | s 屬於 L 或 s 屬於 M}
兩個語言 L 和 M 的連線寫成

LM = {st | s 屬於 L 且 t 屬於 M}
語言 L 的 Kleene 閉包寫成

L* = 語言 L 的零次或多次出現。

表示法

如果 r 和 s 是表示語言 L(r) 和 L(s) 的正則表示式，則

並集：(r)|(s) 是表示 L(r) U L(s) 的正則表示式
連線：(r)(s) 是表示 L(r)L(s) 的正則表示式
Kleene 閉包：(r)* 是表示 (L(r))* 的正則表示式
(r) 是表示 L(r) 的正則表示式

優先順序和結合性

*, 連線(.) 和 | (管道符號) 都是左結合的
* 具有最高優先順序
連線(.) 具有第二高優先順序。
| (管道符號) 具有最低優先順序。

用正則表示式表示語言的有效標記

如果 x 是正則表示式，則

x* 表示 x 的零次或多次出現。

即，它可以生成 { e, x, xx, xxx, xxxx, … }
x+ 表示 x 的一次或多次出現。

即，它可以生成 { x, xx, xxx, xxxx … } 或 x.x*
x? 表示 x 的最多一次出現

即，它可以生成 {x} 或 {e}。

[a-z] 是英語語言的所有小寫字母。

[A-Z] 是英語語言的所有大寫字母。

[0-9] 是數學中使用的所有自然數字。

用正則表示式表示符號的出現

letter = [a – z] 或 [A – Z]

digit = 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 或 [0-9]

sign = [ + | - ]

用正則表示式表示語言標記

Decimal = (sign)^?(digit)⁺

Identifier = (letter)(letter | digit)*

詞法分析器唯一剩下的問題是如何驗證用於指定語言關鍵字模式的正則表示式的有效性。一個被廣泛接受的解決方案是使用有限自動機進行驗證。

有限自動機

有限自動機是一種狀態機，它以符號字串作為輸入並相應地改變其狀態。有限自動機是正則表示式的識別器。當一個正則表示式字串被輸入到有限自動機時，它會為每個字元改變其狀態。如果輸入字串被成功處理並且自動機到達其最終狀態，則它被接受，即剛剛輸入的字串被認為是當前語言的有效標記。

有限自動機的數學模型由以下部分組成

有限的狀態集 (Q)
有限的輸入符號集 (Σ)
一個起始狀態 (q0)
最終狀態集 (qf)
轉移函式 (δ)

轉移函式 (δ) 將有限的狀態集 (Q) 對映到有限的輸入符號集 (Σ)，Q × Σ ➔ Q

有限自動機的構造

設 L(r) 是被某個有限自動機 (FA) 識別的正則語言。

狀態：FA 的狀態用圓圈表示。狀態名稱寫在圓圈內。
起始狀態：自動機開始執行的狀態稱為起始狀態。起始狀態有一個指向它的箭頭。
中間狀態：所有中間狀態至少有兩個箭頭；一個指向它，另一個從它指向出去。
最終狀態：如果輸入字串被成功解析，則預期自動機將處於此狀態。最終狀態用雙圓圈表示。它可以有任意奇數個指向它的箭頭和偶數個從它指向出去的箭頭。奇數箭頭的數量比偶數箭頭多一個，即奇數 = 偶數 + 1。
轉移：當在輸入中找到所需的符號時，就會發生從一個狀態到另一個狀態的轉移。在轉移時，自動機可以移動到下一個狀態或保持在同一狀態。從一個狀態到另一個狀態的移動用有向箭頭表示，其中箭頭指向目標狀態。如果自動機保持在同一狀態，則繪製一個從狀態指向自身的箭頭。

示例：我們假設 FA 接受任何以數字 1 結尾的三位二進位制值。FA = {Q(q₀, q_f), Σ(0,1), q₀, q_f, δ}

最長匹配規則

當詞法分析器讀取原始碼時，它逐個掃描程式碼；當遇到空格、運算子符號或特殊符號時，它會確定一個單詞已完成。

例如

int intvalue;

在掃描到“int”之前的兩個詞法單元時，詞法分析器無法確定它是一個關鍵字int還是識別符號 int 值的開頭。

最長匹配規則規定，應根據所有可用標記中最長的匹配來確定掃描到的詞法單元。

詞法分析器還遵循規則優先順序，其中語言的保留字（例如，關鍵字）優先於使用者輸入。也就是說，如果詞法分析器找到與任何現有保留字匹配的詞法單元，它應該生成錯誤。

編譯器設計 - 語法分析

語法分析或解析是編譯器的第二階段。在本章中，我們將學習構建解析器中使用的基本概念。

我們已經看到，詞法分析器可以在正則表示式和模式規則的幫助下識別標記。但是，由於正則表示式的侷限性，詞法分析器無法檢查給定句子的語法。正則表示式無法檢查平衡標記，例如括號。因此，此階段使用上下文無關文法 (CFG)，它由下推自動機識別。

另一方面，CFG 是正則文法的超集，如下所示

這意味著每個正則文法也是上下文無關的，但存在一些正則文法無法解決的問題。CFG 是描述程式語言語法的有用工具。

上下文無關文法

在本節中，我們將首先了解上下文無關文法的定義，並介紹解析技術中使用的術語。

上下文無關文法有四個組成部分

一組非終結符 (V)。非終結符是表示字串集的語法變數。非終結符定義了幫助定義由文法生成的語言的字串集。
一組標記，稱為終結符 (Σ)。終結符是從中形成字串的基本符號。
一組產生式 (P)。文法的產生式指定了如何組合終結符和非終結符以形成字串。每個產生式都包含一個稱為產生式左側的非終結符、一個箭頭以及一系列標記和/或非終結符，稱為產生式的右側。
其中一個非終結符被指定為起始符號 (S)；從這裡開始產生。

透過重複地用產生式的右側替換一個非終結符（最初是起始符號），可以從起始符號推匯出字串，用於該非終結符。

示例

我們以迴文語言的問題為例，它不能用正則表示式來描述。也就是說，L = { w | w = w^R } 不是正則語言。但它可以用 CFG 來描述，如下所示

G = ( V, Σ, P, S )

其中

V = { Q, Z, N }
Σ = { 0, 1 }
P = { Q → Z | Q → N | Q → ℇ | Z → 0Q0 | N → 1Q1 }
S = { Q }

此文法描述了迴文語言，例如：1001、11100111、00100、1010101、11111 等。

語法分析器

語法分析器或解析器以標記流的形式獲取來自詞法分析器的輸入。解析器根據產生式規則分析原始碼（標記流），以檢測程式碼中的任何錯誤。此階段的輸出是語法樹。

這樣，解析器完成了兩項任務，即解析程式碼，查詢錯誤並將語法樹作為該階段的輸出。

即使程式中存在一些錯誤，也期望解析器解析整個程式碼。解析器使用錯誤恢復策略，我們將在本章後面學習這些策略。

推導

推導基本上是一系列產生式規則，用於獲取輸入字串。在解析過程中，我們對輸入的一些句子形式做出兩個決定

確定要替換的非終結符。
確定用於替換非終結符的產生式規則。

為了確定用產生式規則替換哪個非終結符，我們可以有兩個選擇。

最左推導

如果掃描輸入的句子形式並從左到右替換，則稱為最左推導。由最左推導推匯出的句子形式稱為最左句子形式。

最右推導

如果我們從右到左使用產生式規則掃描和替換輸入，則稱為最右推導。由最右推導推匯出的句子形式稱為最右句子形式。

示例

產生式規則

E → E + E
E → E * E
E → id

輸入字串：id + id * id

最左推導為

E → E * E
E → E + E * E
E → id + E * E
E → id + id * E
E → id + id * id

請注意，始終首先處理最左側的非終結符。

最右推導為

E → E + E
E → E + E * E
E → E + E * id
E → E + id * id
E → id + id * id

語法樹

語法樹是推導的圖形表示。它方便於檢視如何從起始符號推匯出字串。推導的起始符號成為語法樹的根。讓我們透過上一個主題中的一個示例來了解這一點。

我們採用 a + b * c 的最左推導

最左推導為

E → E * E
E → E + E * E
E → id + E * E
E → id + id * E
E → id + id * id

步驟 1

E → E * E

步驟 2

E → E + E * E

步驟 3

E → id + E * E

步驟 4

E → id + id * E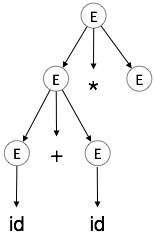

步驟 5

E → id + id * id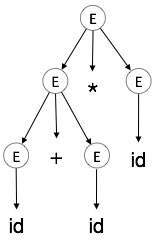

在語法樹中

所有葉子節點都是終結符。
所有內部節點都是非終結符。
中序遍歷給出原始輸入字串。

語法樹描述了運算子的結合性和優先順序。最深的子樹首先被遍歷，因此該子樹中的運算子優先於父節點中的運算子。

解析型別

語法分析器遵循透過上下文無關文法定義的產生式規則。產生式規則的實現方式（推導）將解析分為兩種型別：自頂向下解析和自底向上解析。

自頂向下解析

當解析器從起始符號開始構建語法樹，然後嘗試將起始符號轉換為輸入時，稱為自頂向下解析。

遞迴下降解析：它是自頂向下解析的一種常見形式。它被稱為遞迴，因為它使用遞迴過程來處理輸入。遞迴下降解析存在回溯問題。
回溯：這意味著，如果一個產生式的推導失敗，語法分析器會使用相同產生式的不同規則重新開始該過程。這種技術可能會多次處理輸入字串以確定正確的產生式。

自底向上分析

顧名思義，自底向上分析從輸入符號開始，嘗試構建語法樹直至開始符號。

示例

輸入字串：a + b * c

產生式規則

S → E
E → E + T
E → E * T
E → T
T → id

讓我們開始自底向上分析

a + b * c

讀取輸入並檢查是否有任何產生式與輸入匹配

a + b * c
T + b * c
E + b * c
E + T * c
E * c
E * T
E
S

二義性

如果一個語法 G 對於至少一個字串具有多個語法樹（左推導或右推導），則稱該語法 G 是二義性的。

示例

E → E + E
E → E – E
E → id

對於字串 id + id – id，上述語法生成兩棵語法樹

由二義性語法生成的語言被稱為固有二義性。語法中的二義性對於編譯器構造不利。沒有方法可以自動檢測和消除二義性，但可以透過以下兩種方法之一消除：重寫整個語法以消除二義性，或設定並遵循結合性和優先順序約束。

結合性

如果一個運算元兩側都有運算子，則運算子作用於該運算元的哪一側由這些運算子的結合性決定。如果運算子是左結合的，則運算元將被左側運算子獲取；如果運算子是右結合的，則右側運算子將獲取運算元。

示例

加法、乘法、減法和除法等運算子是左結合的。如果表示式包含

id op id op id

它將被評估為

(id op id) op id

例如，(id + id) + id

像冪運算這樣的運算子是右結合的，即在同一表示式中的計算順序將是

id op (id op id)

例如，id ^ (id ^ id)

優先順序

如果兩個不同的運算子共享一個共同的運算元，則運算子的優先順序決定哪個運算子將獲取該運算元。也就是說，2+3*4 可以有兩個不同的語法樹，一個對應於 (2+3)*4，另一個對應於 2+(3*4)。透過設定運算子之間的優先順序，可以很容易地解決這個問題。如前例所示，在數學上 *（乘法）優先於 +（加法），因此表示式 2+3*4 將始終解釋為

2 + (3 * 4)

這些方法降低了語言或其語法中出現二義性的可能性。

左遞迴

如果一個語法存在任何非終結符 'A'，其推導包含 'A' 本身作為最左邊的符號，則該語法成為左遞迴的。左遞迴語法被認為是自頂向下分析器存在問題的情況。自頂向下分析器從開始符號開始進行分析，開始符號本身是非終結符。因此，當分析器在其推導中遇到相同的非終結符時，它很難判斷何時停止分析左非終結符，從而陷入無限迴圈。

示例

(1) A => Aα | β

(2) S => Aα | β 
    A => Sd

(1) 是直接左遞迴的一個例子，其中 A 是任何非終結符，α 表示非終結符的字串。

(2) 是間接左遞迴的一個例子。

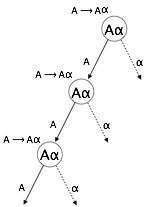
自頂向下分析器將首先分析 A，這反過來將產生一個包含 A 本身的字串，並且分析器可能會永遠陷入迴圈。

消除左遞迴

消除左遞迴的一種方法是使用以下技術

產生式

A => Aα | β

轉換為以下產生式

A => βA’
A => αA’ | ε

這不會影響從語法中推匯出的字串，但它消除了直接左遞迴。

第二種方法是使用以下演算法，該演算法應該消除所有直接和間接左遞迴。

Algorithm
START
Arrange non-terminals in some order like A1, A2, A3,…, An
for each i from 1 to n
{
for each j from 1 to i-1
   {
   replace each production of form Ai⟹Aj𝜸
   with Ai ⟹ δ1𝜸  | δ2𝜸 | δ3𝜸 |…| 𝜸 
   where Aj ⟹ δ1 | δ2|…| δn  are current Aj productions
}
   }
   eliminate immediate left-recursion
END

示例

產生式集

S => Aα | β 
A => Sd

應用上述演算法後，應該變為

S => Aα | β 
A => Aαd | βd

然後，使用第一種技術消除直接左遞迴。

A => βdA’
A => αdA’ | ε

現在，沒有一個產生式具有直接或間接左遞迴。

左因子化

如果多個語法產生式規則具有相同的公共字首字串，則自頂向下分析器無法選擇應該使用哪個產生式來分析手頭的字串。

示例

如果自頂向下分析器遇到如下產生式

A ⟹ αβ | α𝜸 | …

那麼它無法確定要遵循哪個產生式來分析字串，因為兩個產生式都從相同的終結符（或非終結符）開始。為了消除這種混淆，我們使用一種稱為左因子化的技術。

左因子化轉換語法以使其對自頂向下分析器有用。在這種技術中，我們為每個公共字首建立一個產生式，其餘的推導由新的產生式新增。

示例

上述產生式可以寫成

A => αA’
A’=> β | 𝜸 | …

現在，分析器每個字首只有一個產生式，這使得決策更容易。

FIRST 集和 FOLLOW 集

分析表構建的重要部分是建立 FIRST 集和 FOLLOW 集。這些集合可以提供任何終結符在推導中的實際位置。這是為了建立分析表，其中 T[A, t] = α 的替換決策與某個產生式規則相關聯。

FIRST 集

建立此集合是為了瞭解非終結符在第一個位置推匯出的什麼終結符符號。例如，

α → t β

即 α 在第一個位置推匯出 t（終結符）。因此，t ∈ FIRST(α)。

計算 FIRST 集的演算法

檢視 FIRST(α) 集的定義

如果 α 是終結符，則 FIRST(α) = { α }。
如果 α 是非終結符，並且 α → ℇ 是一個產生式，則 FIRST(α) = { ℇ }。
如果 α 是非終結符，並且 α → 𝜸1 𝜸2 𝜸3 … 𝜸n 且任何 FIRST(𝜸) 包含 t，則 t 在 FIRST(α) 中。

FIRST 集可以看作：FIRST(α) = { t | α →^* t β } ∪ { ℇ | α →^* ε}

FOLLOW 集

同樣，我們計算在產生式規則中緊隨非終結符 α 之後的什麼終結符符號。我們不考慮非終結符可以生成什麼，而是檢視緊隨非終結符的產生式之後的下一個終結符符號是什麼。

計算 FOLLOW 集的演算法

如果 α 是開始符號，則 FOLLOW() = $
如果 α 是非終結符，並且有一個產生式 α → AB，則 FIRST(B) 在 FOLLOW(A) 中，除了 ℇ。
如果 α 是非終結符，並且有一個產生式 α → AB，其中 B ℇ，則 FOLLOW(A) 在 FOLLOW(α) 中。

FOLLOW 集可以看作：FOLLOW(α) = { t | S *αt*}

錯誤恢復策略

分析器應該能夠檢測並報告程式中的任何錯誤。預期的是，當遇到錯誤時，分析器應該能夠處理它並繼續分析其餘的輸入。大多數情況下，期望分析器檢查錯誤，但錯誤可能在編譯過程的各個階段遇到。程式在各個階段可能出現以下幾種錯誤

詞法：某些識別符號的名稱輸入錯誤
語法：缺少分號或括號不匹配
語義：不相容的值賦值
邏輯：程式碼不可達，無限迴圈

分析器中可以實現四種常見的錯誤恢復策略來處理程式碼中的錯誤。

恐慌模式

當分析器在語句中的任何位置遇到錯誤時，它會忽略語句的其餘部分，不處理從錯誤輸入到分隔符（如分號）的輸入。這是最簡單的錯誤恢復方法，並且還可以防止分析器陷入無限迴圈。

語句模式

當分析器遇到錯誤時，它會嘗試採取糾正措施，以便語句的其餘輸入允許分析器繼續解析。例如，插入缺少的分號，用分號替換逗號等。分析器設計人員必須在這裡小心，因為一個錯誤的更正可能會導致無限迴圈。

錯誤產生式

編譯器設計人員知道程式碼中可能出現一些常見的錯誤。此外，設計人員可以建立增強的語法以供使用，作為在遇到這些錯誤時生成錯誤構造的產生式。

全域性校正

分析器將手頭的程式視為一個整體，並嘗試弄清楚程式的意圖，並嘗試找到一個最接近的無錯誤匹配。當輸入（語句）X 錯誤時，它會為某個最接近的無錯誤語句 Y 建立語法樹。這可以讓分析器對原始碼進行最小更改，但由於該策略的複雜性（時間和空間），它尚未在實踐中實現。

抽象語法樹

語法樹表示不容易被編譯器解析，因為它們包含比實際需要的更多細節。以下面的語法樹為例

如果仔細觀察，我們會發現大多數葉子節點都是其父節點的單個子節點。此資訊可以在將其饋送到下一階段之前消除。透過隱藏額外資訊，我們可以獲得如下所示的樹

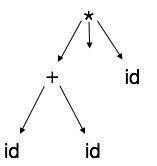
抽象樹可以表示為

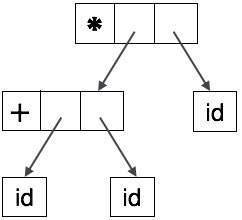
AST 是編譯器中重要的資料結構，包含最少的不必要資訊。AST 比語法樹更緊湊，並且可以很容易地被編譯器使用。

語法分析器的侷限性

語法分析器以標記的形式從詞法分析器接收其輸入。詞法分析器負責語法分析器提供的標記的有效性。語法分析器具有以下缺點

它無法確定標記是否有效，
它無法確定標記是否在使用前已宣告，
它無法確定標記是否在使用前已初始化，
它無法確定對標記型別執行的操作是否有效。

這些任務由語義分析器完成，我們將在語義分析中學習。

編譯器設計 - 語義分析

我們已經瞭解了分析器如何在語法分析階段構建語法樹。在該階段構建的普通語法樹通常對編譯器沒有用，因為它不包含任何關於如何評估樹的資訊。上下文無關語法的產生式，它構成了語言的規則，不包含如何解釋它們。

例如

E → E + T

上述 CFG 產生式沒有與其關聯的語義規則，它不能幫助理解產生式。

語義

語言的語義為其結構（如標記和語法結構）提供含義。語義有助於解釋符號、它們的型別以及它們彼此之間的關係。語義分析判斷源程式中構建的語法結構是否有意義。

CFG + semantic rules = Syntax Directed Definitions

例如

int a = “value”;

不應該在詞法和語法分析階段發出錯誤，因為它在詞法上和結構上都是正確的，但它應該生成語義錯誤，因為賦值的型別不同。這些規則由語言的語法設定，並在語義分析中進行評估。語義分析中應執行以下任務

作用域解析
型別檢查
陣列邊界檢查

語義錯誤

我們之前提到了一些語義分析器預期要識別的語義錯誤。

型別不匹配
未宣告的變數
保留識別符號誤用。
在一個作用域內多次宣告變數。
訪問超出作用域的變數。
實際引數和形式引數不匹配。

屬性文法

屬性文法是上下文無關文法的特殊形式，其中一些附加資訊（屬性）被附加到一個或多個非終結符上，以提供上下文相關的資訊。每個屬性都有明確定義的值域，例如整數、浮點數、字元、字串和表示式。

屬性文法是為上下文無關文法提供語義的一種方法，它可以幫助指定程式語言的語法和語義。屬性文法（當被視為語法樹時）可以在樹的節點之間傳遞值或資訊。

示例

E → E + T { E.value = E.value + T.value }

CFG 的右部包含指定如何解釋文法的語義規則。在這裡，非終結符 E 和 T 的值相加，結果複製到非終結符 E。

語義屬性可以在解析時從其域中分配其值，並在賦值或條件時進行評估。根據屬性獲取值的方式，可以將其大致分為兩類：綜合屬性和繼承屬性。

綜合屬性

這些屬性從其子節點的屬性值獲取值。為了說明，假設以下產生式

S → ABC

如果 S 從其子節點 (A,B,C) 獲取值，則稱其為綜合屬性，因為 ABC 的值被綜合到 S 中。

就像我們之前的例子 (E → E + T) 一樣，父節點 E 從其子節點獲取其值。綜合屬性永遠不會從其父節點或任何兄弟節點獲取值。

繼承屬性

與綜合屬性相反，繼承屬性可以從父節點和/或兄弟節點獲取值。就像以下產生式一樣，

S → ABC

A 可以從 S、B 和 C 獲取值。B 可以從 S、A 和 C 獲取值。同樣，C 可以從 S、A 和 B 獲取值。

擴充套件：當非終結符根據語法規則擴充套件為終結符時

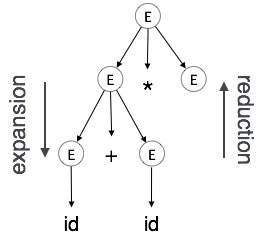
歸約：當終結符根據語法規則歸約為其對應的非終結符時。語法樹自頂向下、從左到右解析。每當發生歸約時，我們都會應用其相應的語義規則（動作）。

語義分析使用語法制導翻譯來執行上述任務。

語義分析器從其前一階段（語法分析）接收 AST（抽象語法樹）。

語義分析器將屬性資訊附加到 AST，這些資訊稱為帶屬性的 AST。

屬性是兩個元組值，<屬性名稱，屬性值>

例如

int value  = 5;
<type, “integer”>
<presentvalue, “5”>

對於每個產生式，我們都附加一個語義規則。

S 屬性 SDT

如果 SDT 僅使用綜合屬性，則稱為 S 屬性 SDT。這些屬性使用 S 屬性 SDT 進行評估，這些 SDT 的語義操作寫在產生式（右側）之後。

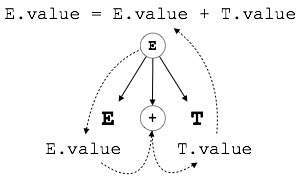
如上所示，S 屬性 SDT 中的屬性在自底向上解析中進行評估，因為父節點的值取決於子節點的值。

L 屬性 SDT

這種形式的 SDT 使用綜合屬性和繼承屬性，但不能從右側兄弟節點獲取值。

在 L 屬性 SDT 中，非終結符可以從其父節點、子節點和兄弟節點獲取值。就像以下產生式一樣

S → ABC

S 可以從 A、B 和 C 獲取值（綜合）。A 只能從 S 獲取值。B 可以從 S 和 A 獲取值。C 可以從 S、A 和 B 獲取值。沒有非終結符可以從其右側的兄弟節點獲取值。

L 屬性 SDT 中的屬性以深度優先和從左到右的解析方式進行評估。

我們可以得出結論，如果一個定義是 S 屬性的，那麼它也是 L 屬性的，因為 L 屬性定義包含 S 屬性定義。

編譯器設計 - 解析器

在上一章中，我們瞭解瞭解析中涉及的基本概念。在本章中，我們將學習可用的各種解析器構造方法。

根據語法樹的構建方式，可以將解析定義為自頂向下或自底向上。

自頂向下解析

我們在上一章中瞭解到，自頂向下解析技術解析輸入，並從根節點開始構建語法樹，逐漸向下移動到葉子節點。自頂向下解析的型別如下所示

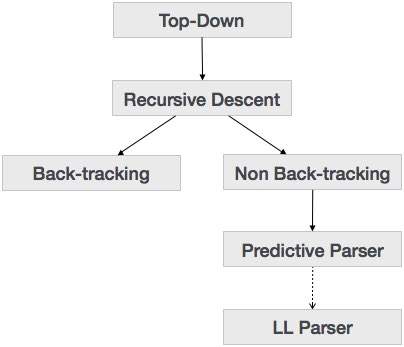
遞迴下降解析

遞迴下降是一種自頂向下的解析技術，它從頂部構建語法樹，並且輸入從左到右讀取。它對每個終結符和非終結符實體使用過程。這種解析技術遞迴地解析輸入以生成語法樹，這可能需要也可能不需要回溯。但與其相關的語法（如果未進行左因子化）無法避免回溯。一種不需要任何回溯的遞迴下降解析形式稱為預測分析。

這種解析技術被認為是遞迴的，因為它使用本質上是遞迴的上下文無關語法。

回溯

自頂向下的解析器從根節點（開始符號）開始，並將輸入字串與產生式規則匹配以替換它們（如果匹配）。要了解這一點，請以以下 CFG 示例為例

S → rXd | rZd
X → oa | ea
Z → ai

對於輸入字串：read，自頂向下的解析器將表現如下

它將從產生式規則中的 S 開始，並將它的匯出與輸入的最左側字母（即“r”）匹配。S 的產生式 (S → rXd) 與它匹配。因此，自頂向下的解析器前進到下一個輸入字母（即“e”）。解析器嘗試擴充套件非終結符“X”並從左側檢查其產生式 (X → oa)。它與下一個輸入符號不匹配。因此，自頂向下的解析器回溯以獲取 X 的下一個產生式規則 (X → ea)。

現在解析器以有序的方式匹配所有輸入字母。字串被接受。

預測分析器

預測分析器是一種遞迴下降解析器，它能夠預測要使用哪個產生式來替換輸入字串。預測分析器不會遇到回溯問題。

為了完成其任務，預測分析器使用一個前瞻指標，該指標指向下一個輸入符號。為了使解析器免於回溯，預測分析器對語法施加了一些約束，並且只接受稱為 LL(k) 語法的語法類別。

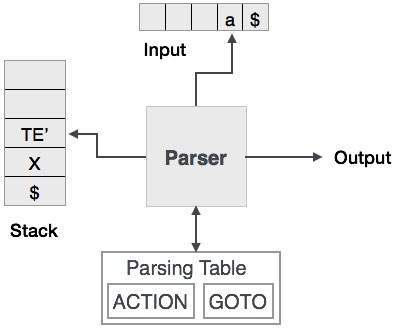
預測分析使用堆疊和解析表來解析輸入並生成語法樹。堆疊和輸入都包含一個結束符號$，以表示堆疊為空並且輸入已消耗。解析器參考解析表來根據輸入和堆疊元素組合做出任何決定。

在遞迴下降解析中，解析器可能有多個產生式可供單個輸入例項選擇，而在預測分析中，每個步驟最多隻有一個產生式可供選擇。在某些情況下，可能沒有產生式與輸入字串匹配，導致解析過程失敗。

LL 解析器

LL 解析器接受 LL 語法。LL 語法是上下文無關語法的子集，但有一些限制以獲得簡化版本，以便於實現。LL 語法可以透過兩種演算法來實現，即遞迴下降或表驅動。

LL 解析器表示為 LL(k)。LL(k) 中的第一個 L 表示從左到右解析輸入，LL(k) 中的第二個 L 表示最左推導，k 本身表示前瞻的數量。通常 k = 1，因此 LL(k) 也可寫成 LL(1)。

LL 解析演算法

我們可以堅持使用確定性 LL(1) 來解釋解析器，因為表的尺寸會隨著 k 的值呈指數增長。其次，如果給定的語法不是 LL(1)，那麼通常它也不是 LL(k)，對於任何給定的 k。

以下是 LL(1) 解析的演算法

Input: 
string ω 
parsing table M for grammar G
Output:
   If ω is in L(G) then left-most derivation of ω,
   error otherwise.

Initial State : $S on stack (with S being start symbol)
   ω$ in the input buffer

SET ip to point the first symbol of ω$.
repeat
let X be the top stack symbol and a the symbol pointed by ip.
if X∈ V_t or $
if X = a
   POP X and advance ip.
	else
   error()
 	endif
else	/* X is non-terminal */
   if M[X,a] = X → Y1, Y2,... Yk    
POP X
PUSH Yk, Yk-1,... Y1 /* Y1 on top */
   Output the production X → Y1, Y2,... Yk 
   else
   error()
   endif
	endif
until X = $	/* empty stack */

如果 G 是 LL(1) 語法，並且 A-> alpha | b 是 G 的兩個不同的產生式

對於任何終結符，alpha 和 beta 都不能匯出以 a 開頭的字串。
alpha 和 beta 中最多隻有一個可以匯出空字串。
如果 beta=> t，則 alpha 不能匯出以 FOLLOW(A) 中的終結符開頭的任何字串。

自底向上分析

自底向上解析從樹的葉子節點開始，向上工作直到到達根節點。在這裡，我們從一個句子開始，然後以相反的方式應用產生式規則，以便到達開始符號。下圖顯示了可用的自底向上解析器。

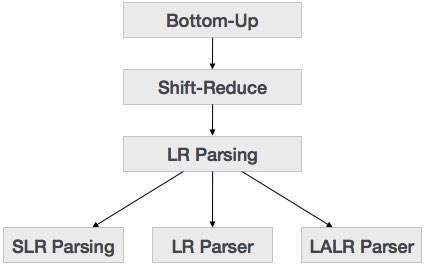
移進-歸約解析

移進-歸約解析使用兩個獨特的步驟進行自底向上解析。這些步驟稱為移進步驟和歸約步驟。

移進步驟：移進步驟指的是輸入指標向下一個輸入符號（稱為移進符號）的推進。此符號被壓入堆疊。移進符號被視為語法樹的單個節點。
歸約步驟：當解析器找到一個完整的語法規則（RHS）並將其替換為（LHS）時，稱為歸約步驟。當堆疊頂部包含一個控制代碼時，就會發生這種情況。為了歸約，對堆疊執行 POP 函式，該函式彈出控制代碼並將其替換為 LHS 非終結符。

LR 解析器

LR 解析器是一種非遞迴的、移進-歸約的、自底向上的解析器。它使用廣泛的上下文無關語法類別，這使其成為最有效的語法分析技術。LR 解析器也稱為 LR(k) 解析器，其中 L 表示從左到右掃描輸入流；R 表示反向構建最右推導，k 表示用於決策的前瞻符號的數量。

有三種廣泛使用的演算法可用於構建 LR 解析器

SLR(1) – 簡單 LR 解析器
- 適用於最小的語法類別
- 狀態數量少，因此表非常小
- 簡單且構建速度快
LR(1) – LR 解析器
- 適用於完整的 LR(1) 語法集
- 生成大型表和大量狀態
- 構建速度慢
LALR(1) – 前瞻 LR 解析器
- 適用於中等大小的語法
- 狀態數量與 SLR(1) 中相同

LR 解析演算法

這裡我們描述了 LR 解析器的骨架演算法

token = next_token()
repeat forever
   s = top of stack
   if action[s, token] = “shift si” then
   PUSH token
   PUSH si 
   token = next_token()
else if action[s, tpken] = “reduce A::= β“ then 
   POP 2 * |β| symbols
   s = top of stack
   PUSH A
	PUSH goto[s,A]
else if action[s, token] = “accept” then
	return
	else
   error()

LL 與 LR

LL	LR
執行最左推導。	反向執行最右推導。
從堆疊上的根非終結符開始。	以堆疊上的根非終結符結束。
當堆疊為空時結束。	以空堆疊開始。
使用堆疊來指定仍然需要預期什麼。	使用堆疊來指定已經看到了什麼。
自頂向下構建語法樹。	自底向上構建語法樹。
連續地將非終結符從堆疊中彈出，並壓入相應的右側。	嘗試在堆疊上識別右側，將其彈出，並壓入相應的非終結符。
擴充套件非終結符。	歸約非終結符。
當從堆疊中彈出終結符時讀取它。	在將終結符壓入堆疊時讀取它。
語法樹的前序遍歷。	語法樹的後序遍歷。

編譯器設計 - 執行時環境

程式作為原始碼僅僅是文字（程式碼、語句等）的集合，要使其“活”起來，需要在目標機器上執行操作。程式需要記憶體資源來執行指令。程式包含過程、識別符號等的名稱，這些名稱需要在執行時與實際的記憶體位置進行對映。

執行時是指程式正在執行。執行時環境是目標機器的狀態，可能包括軟體庫、環境變數等，以向系統中執行的程序提供服務。

執行時支援系統是一個軟體包，大多與可執行程式本身一起生成，並促進程序與執行時環境之間的通訊。它在程式執行期間負責記憶體分配和釋放。

啟用樹

程式是由若干過程組合而成的指令序列。過程中的指令按順序執行。過程有開始和結束分隔符，其內部的所有內容稱為過程體。過程識別符號和它內部的有限指令序列構成了過程體。

過程的執行稱為啟用。啟用記錄包含呼叫過程所需的所有必要資訊。啟用記錄可能包含以下單元（取決於使用的源語言）。

臨時變數	儲存表示式的臨時值和中間值。
區域性資料	儲存被呼叫過程的區域性資料。
機器狀態	在呼叫過程之前儲存機器狀態，例如暫存器、程式計數器等。
控制鏈	儲存呼叫過程的啟用記錄的地址。
訪問鏈	儲存在區域性作用域之外的資料資訊。
實際引數	儲存實際引數，即用於向被呼叫過程傳送輸入的引數。
返回值	儲存返回值。

每當執行一個過程時，它的啟用記錄都會儲存在棧上，也稱為控制棧。當一個過程呼叫另一個過程時，呼叫者的執行將暫停，直到被呼叫過程完成執行。此時，被呼叫過程的啟用記錄儲存在棧上。

我們假設程式控制以順序方式流動，當呼叫一個過程時，其控制權將轉移到被呼叫過程。當被呼叫過程執行完畢時，它將控制權返回給呼叫者。這種型別的控制流使得更容易以樹的形式表示一系列啟用，稱為**啟用樹**。

為了理解這個概念，我們以一段程式碼為例。

. . .
printf(“Enter Your Name: “);
scanf(“%s”, username);
show_data(username);
printf(“Press any key to continue…”);
. . .
int show_data(char *user)
   {
   printf(“Your name is %s”, username);
   return 0;
   }
. . .

以下是給定程式碼的啟用樹。

現在我們理解了過程是以深度優先的方式執行的，因此棧分配是最適合過程啟用的儲存形式。

儲存分配

執行時環境管理以下實體的執行時記憶體需求

**程式碼**：它被稱為程式的文字部分，在執行時不會改變。它的記憶體需求在編譯時已知。
**過程**：它們的文字部分是靜態的，但以隨機方式呼叫。因此，使用棧儲存來管理過程呼叫和啟用。
**變數**：變數只有在執行時才知道，除非它們是全域性變數或常量。堆記憶體分配方案用於管理變數在執行時的記憶體分配和釋放。

靜態分配

在這種分配方案中，編譯資料繫結到記憶體中的固定位置，並且在程式執行時不會改變。由於記憶體需求和儲存位置是預先知道的，因此不需要用於記憶體分配和釋放的執行時支援包。

棧分配

過程呼叫及其啟用透過棧記憶體分配來管理。它以後進先出 (LIFO) 的方式工作，這種分配策略對於遞迴過程呼叫非常有用。

堆分配

過程的區域性變數只在執行時分配和釋放。堆分配用於動態地為變數分配記憶體，並在變數不再需要時回收它。

除了靜態分配的記憶體區域外，棧和堆記憶體都可以動態且意外地增長和縮小。因此，系統無法為它們提供固定數量的記憶體。

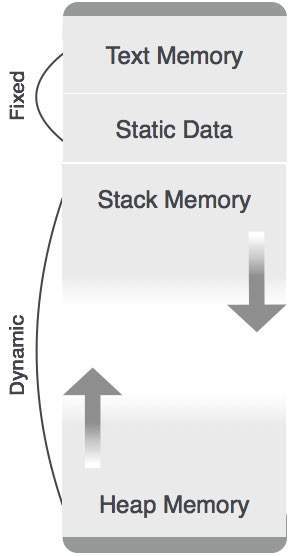
如上圖所示，程式碼的文字部分分配了固定數量的記憶體。棧和堆記憶體排列在分配給程式的總記憶體的兩端。兩者都互相收縮和擴充套件。

引數傳遞

過程之間的通訊媒介稱為引數傳遞。呼叫過程中的變數值透過某種機制傳遞給被呼叫過程。在繼續之前，首先了解一些與程式中值相關的基本術語。

右值 (r-value)

表示式的值稱為其右值。如果單個變量出現在賦值運算子的右側，則該變數包含的值也成為右值。右值始終可以賦值給其他變數。

左值 (l-value)

儲存表示式的記憶體位置（地址）稱為該表示式的左值。它始終出現在賦值運算子的左側。

例如

day = 1;
week = day * 7;
month = 1;
year = month * 12;

從這個例子中，我們理解到像 1、7、12 這樣的常量值，以及像 day、week、month 和 year 這樣的變數，都具有右值。只有變數具有左值，因為它們也表示分配給它們的記憶體位置。

例如

7 = x + y;

是一個左值錯誤，因為常量 7 不表示任何記憶體位置。

形式引數

接收呼叫過程傳遞的資訊的變數稱為形式引數。這些變數在被呼叫函式的定義中宣告。

實際引數

其值或地址被傳遞給被呼叫過程的變數稱為實際引數。這些變數在函式呼叫中作為引數指定。

示例

fun_one()
{
   int actual_parameter = 10;
   call fun_two(int actual_parameter);
}
   fun_two(int formal_parameter)
{
   print formal_parameter;
}

形式引數持有實際引數的資訊，具體取決於所使用的引數傳遞技術。它可能是一個值或一個地址。

傳值呼叫

在傳值呼叫機制中，呼叫過程傳遞實際引數的右值，編譯器將其放入被呼叫過程的啟用記錄中。然後，形式引數持有呼叫過程傳遞的值。如果形式引數持有的值發生更改，則對實際引數沒有任何影響。

傳址呼叫

在傳址呼叫機制中，實際引數的左值被複制到被呼叫過程的啟用記錄中。這樣，被呼叫過程現在擁有實際引數的地址（記憶體位置），形式引數引用相同的記憶體位置。因此，如果形式引數指向的值發生更改，則應在實際引數上看到影響，因為它們也應該指向相同的值。

傳值-恢復呼叫

這種引數傳遞機制與“傳址呼叫”類似，只是實際引數的更改是在被呼叫過程結束時進行的。在函式呼叫時，實際引數的值被複制到被呼叫過程的啟用記錄中。如果對形式引數進行操作，則不會對實際引數產生即時影響（因為傳遞了左值），但當被呼叫過程結束時，形式引數的左值將被複制到實際引數的左值。

示例

int y; 
calling_procedure() 
{
   y = 10;     
   copy_restore(y); //l-value of y is passed
   printf y; //prints 99 
}
copy_restore(int x) 
{     
   x = 99; // y still has value 10 (unaffected)
   y = 0; // y is now 0 
}

當此函式結束時，形式引數 x 的左值將被複制到實際引數 y。即使在過程結束之前更改了 y 的值，x 的左值也會被複制到 y 的左值，使其行為類似於傳址呼叫。

傳名呼叫

像 Algol 這樣的語言提供了一種新的引數傳遞機制，其工作方式類似於 C 語言中的預處理器。在傳名呼叫機制中，被呼叫過程的名稱被其實際主體替換。傳名呼叫在過程呼叫中將引數表示式文字替換為過程主體中相應的引數，以便它現在可以像傳址呼叫一樣處理實際引數。

編譯器設計 - 符號表

符號表是編譯器建立和維護的重要資料結構，用於儲存有關各種實體（例如變數名、函式名、物件、類、介面等）出現的資訊。符號表被編譯器的分析和綜合部分使用。

根據手頭的語言，符號表可以服務於以下目的

在一個地方以結構化的形式儲存所有實體的名稱。
驗證變數是否已宣告。
透過驗證原始碼中的賦值和表示式在語義上是否正確來實現型別檢查。
確定名稱的作用域（作用域解析）。

符號表只是一個表，可以是線性表或雜湊表。它為每個名稱維護一個如下格式的條目

<symbol name,  type,  attribute>

例如，如果符號表必須儲存以下變數宣告的資訊

static int interest;

那麼它應該儲存如下條目

<interest, int, static>

屬性子句包含與名稱相關的條目。

實現

如果編譯器要處理少量資料，則符號表可以實現為無序列表，這很容易編碼，但它只適用於小型表格。符號表可以透過以下幾種方式實現

線性（排序或未排序）列表
二叉搜尋樹
雜湊表

在所有這些中，符號表大多實現為雜湊表，其中原始碼符號本身被視為雜湊函式的鍵，返回值是有關符號的資訊。

運算

符號表（線性或雜湊）應提供以下操作。

insert()

此操作更常被分析階段使用，即編譯器的前半部分，其中識別標記並將名稱儲存在表中。此操作用於在符號表中新增有關原始碼中出現的唯一名稱的資訊。名稱儲存的格式或結構取決於手頭的編譯器。

原始碼中符號的屬性是與該符號關聯的資訊。此資訊包含有關符號的值、狀態、作用域和型別。insert() 函式將符號及其屬性作為引數，並將資訊儲存在符號表中。

例如

int a;

應由編譯器處理為

insert(a, int);

lookup()

lookup() 操作用於在符號表中搜索名稱以確定

符號是否存在於表中。
它是否在使用前已宣告。
名稱是否在作用域中使用。
符號是否已初始化。
符號是否宣告多次。

lookup() 函式的格式根據程式語言而有所不同。基本格式應與以下內容匹配

lookup(symbol)

如果符號不存在於符號表中，則此方法返回 0（零）。如果符號存在於符號表中，則返回儲存在表中的屬性。

作用域管理

編譯器維護兩種型別的符號表：一個**全域性符號表**，所有過程都可以訪問它；以及為程式中的每個作用域建立的**作用域符號表**。

為了確定名稱的作用域，符號表以層次結構排列，如下例所示

. . . 
int value=10;

void pro_one()
   {
   int one_1;
   int one_2;
   
      {              \
      int one_3;      |_  inner scope 1 
      int one_4;      | 
      }              /
      
   int one_5; 
   
      {              \   
      int one_6;      |_  inner scope 2
      int one_7;      |
      }              /
   }
   
void pro_two()
   {
   int two_1;
   int two_2;
   
      {              \
      int two_3;      |_  inner scope 3
      int two_4;      |
      }              /
      
   int two_5;
   }
. . .

上述程式可以用符號表的層次結構表示

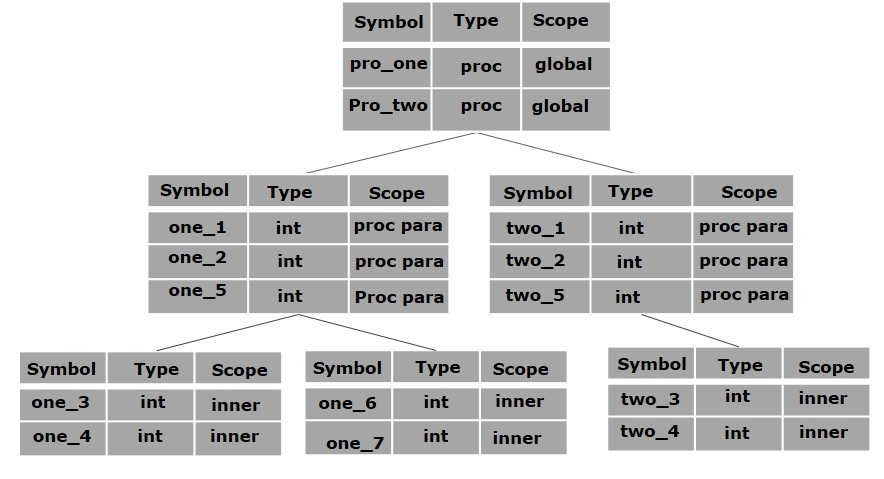
全域性符號表包含一個全域性變數 (int value) 和兩個過程名稱的名稱，這些名稱應該對上面顯示的所有子節點可用。在 pro_one 符號表（及其所有子表）中提到的名稱對於 pro_two 符號及其子表不可用。

此符號表資料結構層次結構儲存在語義分析器中，並且每當需要在符號表中搜索名稱時，都使用以下演算法進行搜尋。

首先，將在當前作用域（即當前符號表）中搜索符號。
如果找到名稱，則搜尋完成，否則將在父符號表中搜索，直到：
找到名稱或全域性符號表已搜尋過該名稱。

編譯器 - 中間程式碼生成

原始碼可以直接轉換為目標機器碼，那麼為什麼還需要將原始碼轉換為中間程式碼，然後再將其轉換為目的碼呢？讓我們看看我們為什麼需要中間程式碼。

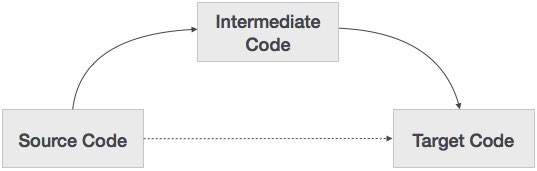
如果編譯器在沒有生成中間程式碼選項的情況下將源語言轉換為其目標機器語言，則對於每臺新機器，都需要一個完整的本地編譯器。
中間程式碼透過保持所有編譯器的分析部分相同，消除了每臺唯一機器都需要一個新的完整編譯器的需求。
編譯器的第二部分，合成，根據目標機器進行更改。
透過在中間程式碼上應用程式碼最佳化技術，更容易應用原始碼修改以提高程式碼效能。

中間表示

中間程式碼可以用多種方式表示，並且它們有各自的優點。

高階IR - 高階中間程式碼表示非常接近源語言本身。它們可以很容易地從原始碼生成，並且我們可以很容易地應用程式碼修改來增強效能。但對於目標機器最佳化，它不太受歡迎。
低階IR - 這種表示形式接近目標機器，這使得它適合暫存器和記憶體分配、指令集選擇等。它有利於機器相關的最佳化。

中間程式碼可以是特定於語言的（例如，Java的位元組碼）或與語言無關的（三地址碼）。

三地址碼

中間程式碼生成器從其前驅階段（語義分析器）接收帶註釋的語法樹形式的輸入。然後可以將該語法樹轉換為線性表示，例如字尾表示法。中間程式碼傾向於與機器無關的程式碼。因此，程式碼生成器假設有無限數量的記憶體儲存（暫存器）來生成程式碼。

例如

a = b + c * d;

中間程式碼生成器將嘗試將此表示式分解為子表示式，然後生成相應的程式碼。

r1 = c * d;
r2 = b + r1;
a = r2

r 在目標程式中用作暫存器。

三地址碼最多有三個地址位置來計算表示式。三地址碼可以用兩種形式表示：四元式和三元式。

四元式

四元式表示中的每個指令都分為四個欄位：運算子、arg1、arg2和結果。以上示例在四元式格式中表示如下

運算子	arg₁	arg₂	結果
*	c	d	r1
+	b	r1	r2
+	r2	r1	r3
=	r3		a

三元式

三元式表示中的每個指令都有三個欄位：運算子、arg1和arg2。各個子表示式的結果由表示式的位序表示。三元式表示與DAG和語法樹的相似性。在表示表示式時，它們等效於DAG。

運算子	arg₁	arg₂
*	c	d
+	b	(0)
+	(1)	(0)
=	(2)

三元式在最佳化時面臨程式碼不可移動的問題，因為結果是位置性的，更改表示式的順序或位置可能會導致問題。

間接三元式

這種表示形式是對三元式表示形式的增強。它使用指標而不是位置來儲存結果。這使最佳化器能夠自由地重新定位子表示式以生成最佳化的程式碼。

宣告

變數或過程必須在使用之前宣告。宣告涉及在記憶體中分配空間以及在符號表中輸入型別和名稱。程式的編碼和設計可以考慮目標機器結構，但並非總是能夠準確地將原始碼轉換為目標語言。

將整個程式視為過程和子過程的集合，就可以宣告所有區域性於過程的名稱。記憶體分配以連續的方式完成，名稱按程式中宣告的順序分配到記憶體。我們使用偏移量變數並將其設定為零{offset = 0}，表示基地址。

源程式語言和目標機器架構在儲存名稱的方式上可能有所不同，因此使用相對定址。當第一個名稱從記憶體位置0 {offset=0}開始分配記憶體時，稍後宣告的下一個名稱應分配到第一個名稱旁邊的記憶體。

示例

我們以C程式語言為例，其中整型變數分配2位元組記憶體，浮點型變數分配4位元組記憶體。

int a;
float b;
Allocation process:
{offset = 0}
int a;
id.type = int
id.width = 2
offset = offset + id.width 
{offset = 2}
float b;
   id.type = float
   id.width = 4
   offset = offset + id.width 
{offset = 6}

為了將此詳細資訊輸入符號表，可以使用過程enter。此方法可能具有以下結構

enter(name, type, offset)

此過程應在符號表中為變數name建立一個條目，其型別設定為type，其資料區域中的相對地址為offset。

編譯器設計 - 程式碼生成

程式碼生成可以被認為是編譯的最後階段。透過程式碼生成後，可以在程式碼上應用最佳化過程，但這可以看作是程式碼生成階段本身的一部分。編譯器生成的程式碼是某種低階程式語言的目的碼，例如組合語言。我們已經看到，用高階語言編寫的原始碼被轉換為低階語言，從而產生低階目的碼，該程式碼應具有以下最低屬性

它應該包含原始碼的確切含義。
它在CPU使用和記憶體管理方面應該高效。

我們現在將瞭解如何將中間程式碼轉換為目標物件程式碼（在本例中為彙編程式碼）。

有向無環圖

有向無環圖（DAG）是一種描繪基本塊結構、幫助檢視值在基本塊之間流動的流程並提供最佳化的工具。DAG 提供了對基本塊的簡單轉換。DAG可以在這裡理解

葉子節點表示識別符號、名稱或常量。
內部節點表示運算子。
內部節點還表示表示式的結果或要儲存或分配值的識別符號/名稱。

示例

t₀ = a + b
t₁ = t₀ + c
d = t₀ + t₁

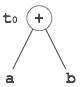
[t₀ = a + b]

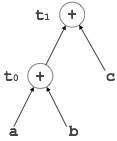
[t₁ = t₀ + c]

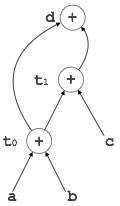
[d = t₀ + t₁]

窺孔最佳化

這種最佳化技術在本地對原始碼進行操作，將其轉換為最佳化程式碼。就本地而言，是指手頭的程式碼塊的一小部分。這些方法既可以應用於中間程式碼，也可以應用於目的碼。分析一堆語句，並檢查以下可能的最佳化

冗餘指令消除

在原始碼級別，使用者可以執行以下操作

int add_ten(int x)
   {
   int y, z;
   y = 10;
   z = x + y;
   return z;
   }

int add_ten(int x)
   {
   int y;
   y = 10;
   y = x + y;
   return y;
   }

int add_ten(int x)
   {
   int y = 10;
   return x + y;
   }

int add_ten(int x)
   {
   return x + 10;
   }

在編譯級別，編譯器搜尋本質上冗餘的指令。即使刪除其中一些指令，多條載入和儲存指令也可能具有相同的含義。例如

MOV x, R0
MOV R0, R1

我們可以刪除第一條指令並將句子重寫為

MOV x, R1

不可達程式碼

不可達程式碼是程式程式碼的一部分，由於程式設計結構而永遠不會被訪問。程式設計師可能意外地編寫了一段永遠無法到達的程式碼。

示例

void add_ten(int x)
{
   return x + 10;
   printf(“value of x is %d”, x);
}

在此程式碼段中，printf語句將永遠不會執行，因為程式控制在執行之前返回，因此可以刪除printf。

控制流最佳化

在程式碼中，程式控制在來回跳轉而沒有執行任何重要任務的情況。可以刪除這些跳轉。考慮以下程式碼塊

...		
MOV R1, R2
GOTO L1
...
L1 :   GOTO L2
L2 :   INC R1

在此程式碼中，可以刪除標籤L1，因為它將控制權傳遞給L2。因此，控制權可以直接到達L2，而不是跳轉到L1然後跳轉到L2，如下所示

...		
MOV R1, R2
GOTO L2
...
L2 :   INC R1

代數表示式化簡

在某些情況下，代數表示式可以簡化。例如，表示式a = a + 0可以用a本身替換，表示式a = a + 1可以簡單地替換為INC a。

強度削弱

有些操作會消耗更多時間和空間。可以透過用其他消耗更少時間和空間但產生相同結果的操作替換它們來降低它們的“強度”。

例如，x * 2可以用x << 1替換，後者僅涉及一次左移。雖然a * a和a²的輸出相同，但a²的實現效率要高得多。

訪問機器指令

目標機器可以部署更復雜的指令，這些指令能夠更有效地執行特定操作。如果目的碼可以直接容納這些指令，那麼這不僅會提高程式碼質量，還會產生更有效的結果。

程式碼生成器

程式碼生成器需要了解目標機器的執行時環境及其指令集。程式碼生成器應考慮以下事項以生成程式碼

目標語言：程式碼生成器必須瞭解要轉換程式碼的目標語言的性質。該語言可能提供一些特定於機器的指令，以幫助編譯器更方便地生成程式碼。目標機器可以具有CISC或RISC處理器架構。
IR型別：中間表示有多種形式。它可以是抽象語法樹（AST）結構、逆波蘭表示法或三地址碼。
指令選擇：程式碼生成器將中間表示作為輸入，並將其轉換為目標機器的指令集。一種表示形式可以有多種方式（指令）進行轉換，因此程式碼生成器有責任明智地選擇合適的指令。
暫存器分配：程式在執行期間需要維護許多值。目標機器的架構可能不允許所有值都儲存在CPU記憶體或暫存器中。程式碼生成器決定將哪些值儲存在暫存器中。此外，它還決定使用哪些暫存器來儲存這些值。
指令排序：最後，程式碼生成器決定指令執行的順序。它為指令建立排程以執行它們。

描述符

程式碼生成器在生成程式碼時必須同時跟蹤暫存器（用於可用性）和地址（值的儲存位置）。對於這兩者，都使用以下兩個描述符

暫存器描述符：暫存器描述符用於告知程式碼生成器暫存器的可用性。暫存器描述符跟蹤儲存在每個暫存器中的值。每當在程式碼生成期間需要新的暫存器時，都會查詢此描述符以獲取暫存器的可用性。
地址描述符：程式中使用的名稱（識別符號）的值在執行期間可能儲存在不同的位置。地址描述符用於跟蹤儲存識別符號值的記憶體位置。這些位置可能包括 CPU 暫存器、堆、棧、記憶體或上述位置的組合。

程式碼生成器即時更新這兩個描述符。對於載入語句 LD R1, x，程式碼生成器

更新暫存器描述符 R1，其中包含 x 的值，並且
更新地址描述符 (x) 以顯示 x 的一個例項位於 R1 中。

程式碼生成

基本塊包含一系列三地址指令。程式碼生成器將這些指令序列作為輸入。

注意：如果名稱的值在多個位置（暫存器、快取或記憶體）中找到，則暫存器的值將優先於快取和主記憶體。同樣，快取的值將優先於主記憶體。主記憶體幾乎沒有優先順序。

getReg：程式碼生成器使用getReg函式來確定可用暫存器的狀態和名稱值的儲存位置。getReg的工作原理如下

如果變數 Y 已經存在於暫存器 R 中，則使用該暫存器。
否則，如果某個暫存器 R 可用，則使用該暫存器。
否則，如果以上兩種選項都不可能，則選擇需要最少載入和儲存指令的暫存器。

對於指令 x = y OP z，程式碼生成器可以執行以下操作。假設 L 是要儲存 y OP z 輸出的位置（最好是暫存器）

呼叫函式 getReg，以確定 L 的位置。
透過查詢y的地址描述符來確定y的當前位置（暫存器或記憶體）。如果y當前不在暫存器L中，則生成以下指令以將y的值複製到L

MOV y’，L

其中y’表示y的複製值。
使用與步驟 2 中對y相同的方法確定z的當前位置，並生成以下指令

OP z’，L

其中z’表示z的複製值。
現在 L 包含 y OP z 的值，該值旨在分配給x。因此，如果 L 是一個暫存器，則更新其描述符以指示它包含x的值。更新x的描述符以指示它儲存在位置L處。
如果 y 和 z 以後不再使用，則可以將其返還給系統。

其他程式碼結構（如迴圈和條件語句）以一般的彙編方式轉換為組合語言。

編譯器設計 - 程式碼最佳化

最佳化是一種程式轉換技術，它試圖透過減少程式碼消耗的資源（即 CPU、記憶體）並提高速度來改進程式碼。

在最佳化中，高階通用程式設計結構被替換為非常高效的低階程式設計程式碼。程式碼最佳化過程必須遵循以下三個規則

輸出程式碼絕不能以任何方式更改程式的含義。
最佳化應提高程式的速度，如果可能，程式應要求更少的資源。
最佳化本身應該很快，並且不應延遲整個編譯過程。

可以在編譯過程的各個級別進行最佳化程式碼的努力。

在開始時，使用者可以更改/重新排列程式碼或使用更好的演算法來編寫程式碼。
在生成中間程式碼後，編譯器可以透過地址計算和改進迴圈來修改中間程式碼。
在生成目標機器程式碼時，編譯器可以利用記憶體層次結構和 CPU 暫存器。

最佳化可以大致分為兩種型別：機器無關和機器相關。

機器無關最佳化

在這種最佳化中，編譯器接收中間程式碼並轉換不涉及任何 CPU 暫存器和/或絕對記憶體位置的程式碼部分。例如

do
{
   item = 10;
   value = value + item; 
}while(value<100);

此程式碼涉及識別符號 item 的重複賦值，如果我們這樣放置

Item = 10;
do
{
   value = value + item; 
} while(value<100);

不僅可以節省 CPU 週期，而且可以在任何處理器上使用。

機器相關最佳化

機器相關最佳化是在生成目的碼後以及根據目標機器架構轉換程式碼時完成的。它涉及 CPU 暫存器，並且可能具有絕對記憶體引用而不是相對引用。機器相關最佳化器努力充分利用記憶體層次結構。

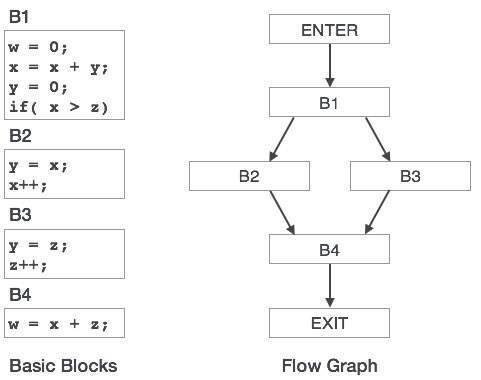
基本塊

原始碼通常包含許多指令，這些指令始終按順序執行，並被視為程式碼的基本塊。這些基本塊之間沒有任何跳轉語句，即，當執行第一條指令時，同一基本塊中的所有指令都將按其出現的順序執行，而不會丟失程式的流程控制。

程式可以具有各種結構作為基本塊，例如 IF-THEN-ELSE、SWITCH-CASE 條件語句和迴圈，如 DO-WHILE、FOR 和 REPEAT-UNTIL 等。

基本塊識別

我們可以使用以下演算法來查詢程式中的基本塊

搜尋所有基本塊的頭部語句，從這些語句開始基本塊
- 程式的第一條語句。
- 任何分支（條件/無條件）的目標語句。
- 任何分支語句之後的語句。
頭部語句及其後的語句構成一個基本塊。
基本塊不包含任何其他基本塊的頭部語句。

基本塊是從程式碼生成和最佳化角度來看的重要概念。

基本塊在識別在單個基本塊中多次使用的變數方面發揮著重要作用。如果任何變數被多次使用，則分配給該變數的暫存器記憶體無需清空，除非塊執行完成。

控制流圖

程式中的基本塊可以透過控制流圖來表示。控制流圖描述了程式控制如何在塊之間傳遞。它是一個有用的工具，有助於透過幫助定位程式中的任何不需要的迴圈來進行最佳化。

迴圈最佳化

大多數程式在系統中以迴圈形式執行。為了節省 CPU 週期和記憶體，有必要最佳化迴圈。迴圈可以透過以下技術進行最佳化

不變程式碼：位於迴圈中並在每次迭代時計算相同值的程式碼片段稱為迴圈不變程式碼。可以透過將其儲存為僅計算一次而不是每次迭代來將其移出迴圈。
歸納分析：如果變數的值在迴圈內透過迴圈不變值更改，則該變數稱為歸納變數。
強度削弱：有一些表示式消耗更多的 CPU 週期、時間和記憶體。這些表示式應替換為更便宜的表示式，而不會影響表示式的輸出。例如，乘法 (x * 2) 在 CPU 週期方面比 (x << 1) 昂貴，並且產生相同的結果。

死程式碼消除

死程式碼是一條或多條程式碼語句，這些語句

要麼從未執行過或無法訪問，
或者如果執行，則其輸出永遠不會被使用。

因此，死程式碼在任何程式操作中都不起作用，因此可以簡單地將其消除。

部分死程式碼

有些程式碼語句的計算值僅在某些情況下使用，即有時使用這些值，有時不使用。此類程式碼稱為部分死程式碼。

上面的控制流圖描述了一塊程式，其中變數“a”用於分配表示式“x * y”的輸出。假設分配給“a”的值在迴圈內從未使用過。在控制離開迴圈後立即，“a”被分配變數“z”的值，該值將在程式中稍後使用。我們在此得出結論，即“a”的賦值程式碼在任何地方都從未使用過，因此有資格被消除。

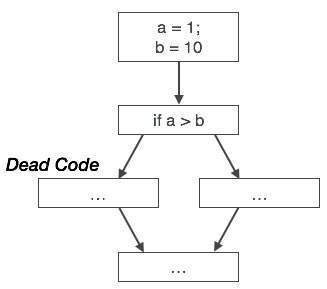
同樣，上圖說明條件語句始終為假，這意味著在真情況下編寫的程式碼將永遠不會執行，因此可以將其刪除。

部分冗餘

冗餘表示式在並行路徑中多次計算，而運算元沒有改變。而部分冗餘表示式在路徑中多次計算，而運算元沒有改變。例如，

[冗餘表示式]

[部分冗餘表示式]

迴圈不變程式碼是部分冗餘的，可以透過使用程式碼移動技術來消除。

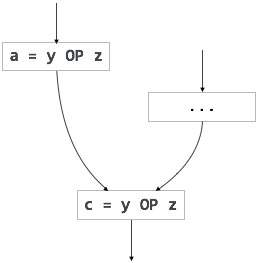
部分冗餘程式碼的另一個例子可以是

If (condition)
{
   a = y OP z;
}
else
{
   ...
}
c = y OP z;

我們假設運算元（y 和z）的值從變數a分配到變數c沒有改變。在這裡，如果條件語句為真，則 y OP z 被計算兩次，否則計算一次。程式碼移動可用於消除這種冗餘，如下所示

If (condition)
{
   ...
   tmp = y OP z;
   a = tmp;
   ...
}
else
{
   ...
   tmp = y OP z;
}
c = tmp;

在這裡，無論條件是真還是假；y OP z 應該只計算一次。

列印頁面