課堂活動（構建“平方根螺旋”）：取一張大紙，按照以下方式構建“平方根螺旋”。從一個點\( \mathrm{O} \)開始，畫一條長度為單位長度的線段\( \mathrm{OP}_{1} \)。畫一條垂直於\( \mathrm{OP}_{1} \)且長度為單位長度的線段\( \mathrm{P}_{1} \mathrm{P}_{2} \)（見下圖）。現在畫一條垂直於\( \mathrm{OP}_{2} \)的線段\( \mathrm{P}_{2} \mathrm{P}_{3} \)。然後畫一條垂直於\( \mathrm{OP}_{3} \)的線段\( \mathrm{P}_{3} \mathrm{P}_{4} \)。以此類推，圖 1.9：構建平方根螺旋您可以透過畫一條垂直於\( \mathrm{OP}_{\mathrm{n}-1} \)且長度為單位長度的線段來得到線段\( \mathrm{P}_{\mathrm{a}-1} \mathrm{P}_{\mathrm{n}} \)。透過這種方式，您將建立點\( \mathrm{P}_{2}, \mathrm{P}_{3}, \ldots, \mathrm{P}_{\mathrm{n}}, \ldots . \)，並連線它們以建立一個美麗的螺旋，描繪了\( \sqrt{2}, \sqrt{3}, \sqrt{4}, \ldots \)
"
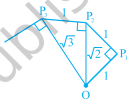待辦事項
我們需要構建一個如題目中所示的平方根螺旋。
解答
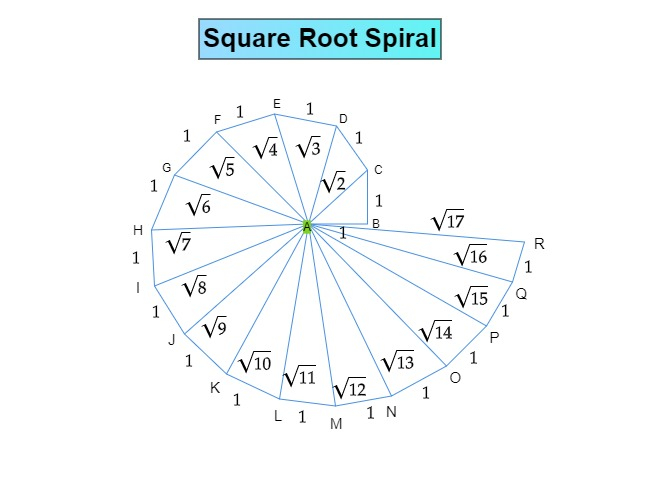
構建步驟
1. 在紙上標記一個點 $A$。
$A$ 是平方根螺旋的中心。
2. 從 $A$ 開始，水平畫一條 $1\ cm$ 長的直線 $AB$。
3. 從 $B$ 開始，畫一條垂直於 $AB$ 且長度為 $1\ cm$ 的直線 $BC$。
4. 連線 $AC$。
$AC^2=AB^2+BC^2$
$AC^2=1^2+1^2$
$AC=\sqrt{2}\ cm$
5. 從 $C$ 開始，畫一條垂直於 $AC$ 且長度為 $1\ cm$ 的直線，並標記端點 $D$。
6. 連線 $AD$。 $AD=\sqrt{3}\ cm$
7. 同理，$AE=\sqrt{4}\ cm, AF=\sqrt5\ cm,.......$
- 相關文章
- 如果點\( P(2,1) \)位於連線點\( A(4,2) \)和\( B(8,4) \)的線段上，則(A) \( \mathrm{AP}=\frac{1}{3} \mathrm{AB} \)(B) \( \mathrm{AP}=\mathrm{PB} \)(C) \( \mathrm{PB}=\frac{1}{3} \mathrm{AB} \)(D) \( \mathrm{AP}=\frac{1}{2} \mathrm{AB} \)
- 如果\( \mathrm{P}(9 a-2,-b) \)將連線\( \mathrm{A}(3 a+1,-3) \)和\( \mathrm{B}(8 a, 5) \)的線段按\( 3: 1 \)的比例分割，求\( a \)和\( b \)的值。
- 在下圖中，\( \mathrm{P} \)是平行四邊形\( \mathrm{ABCD} \)內部的一個點。證明(i) \( \operatorname{ar}(\mathrm{APB})+\operatorname{ar}(\mathrm{PCD})=\frac{1}{2} \operatorname{ar}(\mathrm{ABCD}) \)(ii) \( \operatorname{ar}(\mathrm{APD})+\operatorname{ar}(\mathrm{PBC})=\operatorname{ar}(\mathrm{APB})+\operatorname{ar}(\mathrm{PCD}) \)[提示：過\( \mathrm{P} \)，畫一條平行於\( \mathrm{AB} \)的線段。]""
- \( \mathrm{O} \)是梯形\( \mathrm{ABCD} \)的對角線\( \mathrm{AC} \)和\( \mathrm{BD} \)的交點，其中\( \mathrm{AB} \| \mathrm{DC} \)。過\( \mathrm{O} \)，畫一條平行於\( \mathrm{AB} \)的線段\( \mathrm{PQ} \)，分別交\( \mathrm{AD} \)於\( \mathrm{P} \)和\( \mathrm{BC} \)於\( \mathrm{Q} \)。證明\( \mathrm{PO}=\mathrm{QO} \)。
- 在圖 6.17 中，\( \mathrm{POQ} \)是一條直線。射線\( \mathrm{OR} \)垂直於直線\( \mathrm{PQ} \)。OS 是另一條位於射線\( OP \)和 OR 之間的射線。證明\( \angle \mathrm{ROS}=\frac{1}{2}(\angle \mathrm{QOS}-\angle \mathrm{POS}) \)""
- 畫任意一條線段\( \overline{\mathrm{PQ}} \)。取任意一點\( \mathrm{R} \)，它不線上段上。過\( \mathrm{R} \)，畫一條垂直於\( \overline{\mathrm{PQ}} \)的線段。（使用直尺和三角板）
- 求連線點\( \mathrm{P}(-1,3) \)和\( \mathrm{Q}(2,5) \)的線段上的點\( R \)的座標，使得\( \mathrm{PR}=\frac{3}{5} \mathrm{PQ} \)。
- 畫一條長度為\( 5.5 \mathrm{cm} \)的線段 \( AB \)。線上段上找到一點 \( P \)，使得 \( \overline{A P}=\frac{2}{3} \overline{P B} \)。
- 畫一條長度為\( 9.5 \mathrm{~cm} \)的線段，並作其垂直平分線。
- 畫任意一條線段\( \overline{\mathrm{AB}} \)。線上段上標記任意一點\( \mathrm{M} \)。過\( \mathrm{M} \)，畫一條垂直於\( \overline{\mathrm{AB}} \)的線段。（使用直尺和圓規）
- 從給定的四個選項中選擇正確的答案：如果\( S \)是\( \triangle P Q R \)的邊\( P Q \)上的一點，使得\( P S=Q S=R S \)，則(A) \( \mathrm{PR}, \mathrm{QR}=\mathrm{RS}^{2} \)(B) \( \mathrm{QS}^{2}+\mathrm{RS}^{2}=\mathrm{QR}^{2} \)(C) \( \mathrm{PR}^{2}+\mathrm{QR}^{2}=\mathrm{PQ}^{2} \)(D) \( \mathrm{PS}^{2}+\mathrm{RS}^{2}=\mathrm{PR}^{2} \)
- 兩個全等的圓在點\( \mathrm{A} \)和\( \mathrm{B} \)處相交。過\( \mathrm{A} \)畫任意一條線段\( \mathrm{PAQ} \)，使得\( \mathrm{P}, \mathrm{Q} \)位於兩個圓上。證明\( \mathrm{BP}=\mathrm{BQ} \)。
- 畫一條直線 $l$，並在其上取一點\( \mathrm{X} \)。過\( \mathrm{X} \)，畫一條垂直於 $1$ 的線段\( \overline{\mathrm{XY}} \)。現在，在 Y 處畫一條垂直於\( \overline{X Y} \)的線段。（使用直尺和圓規）
- \( \mathrm{AB} \)是一條線段，\( \mathrm{P} \)是它的中點。\( \mathrm{D} \)和\( \mathrm{E} \)是\( \mathrm{AB} \)同側上的點，使得\( \angle \mathrm{BAD}=\angle \mathrm{ABE} \)且\( \angle \mathrm{EPA}=\angle \mathrm{DPB} \)（見圖 7.22）。證明(i) \( \triangle \mathrm{DAP} \cong \triangle \mathrm{EBP} \)(ii) \( \mathrm{AD}=\mathrm{BE} \)""
- 在下圖中，\( \mathrm{PA}, \mathrm{QB}, \mathrm{RC} \)和\( \mathrm{SD} \)都垂直於直線\( l \)，\( \mathrm{AB}=6 \mathrm{~cm} \)，\( \mathrm{BC}=9 \mathrm{~cm}, CD=12 \mathrm{~cm} \)且\( SP=36 \mathrm{~cm} \)。求\( P Q, Q R \)和\( R S \)。"
資料結構
網路
關係型資料庫管理系統
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理
化學
生物
數學
英語
經濟學
心理學
社會學
時尚研究
法律研究