畫一條線段\( A B=5.5 \mathrm{cm} \)。在該線段上找到一點\( P \),使得\( \overline{A P}=\frac{2}{3} \overline{P B} \)。
已知:\( A B=5.5 \mathrm{cm} \)。\( \overline{A P}=\frac{2}{3} \overline{P B} \)。
求解:線段 AB 上的點\( P \)
解
設 P 為一點,使得 AP=$\frac{2}{3}$PB
=>AP+PB=AB
$\frac{2}{3}$ PB+PB=5.5
$\frac{5}{3}$PB=5.5
PB=3.3cm
AP=2.2cm
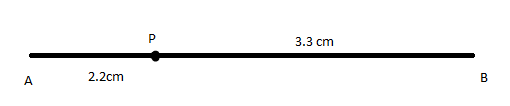
- 相關文章
- 如果\( P A \) 和\( P B \) 是從外一點\( P \) 引出的切線。使得\( P A=10 \mathrm{~cm} \) 且\( \angle A P B=60^{\circ} \)。求弦\( A B \) 的長度。
- 畫任意線段\( \overline{\mathrm{PQ}} \)。不測量\( \overline{\mathrm{PQ}} \),構造\( \overline{\mathrm{PQ}} \) 的副本。
- 畫任意線段\( \overline{\mathrm{AB}} \)。在其上標記任意一點\( \mathrm{M} \)。過\( \mathrm{M} \),畫\( \overline{\mathrm{AB}} \) 的垂線。(使用尺子和圓規)
- 如果 $A$ 和 $B$ 分別是 $(-2, -2)$ 和 $(2, -4)$,則求 $P$ 的座標,使得 $AP = \frac{3}{7}AB$ 且 $P$ 位於線段 $AB$ 上。
- 畫一個以\( O \) 為頂點的任意角。在其中一條射線上取一點\( A \),在另一條射線上取一點\( B \),使得\( \mathrm{OA}=\mathrm{OB} \)。畫\( \overline{\mathrm{OA}} \) 和\( \overline{\mathrm{OB}} \) 的垂直平分線。設它們相交於 P。是否\( \mathrm{PA}=\mathrm{PB} \)?
- 畫一條直線 $l$,並在其上取一點\( \mathrm{X} \)。過\( \mathrm{X} \),畫一條垂直於 $1$ 的線段\( \overline{\mathrm{XY}} \)。現在在 Y 處畫\( \overline{X Y} \) 的垂線。(使用尺子和圓規)
- 畫任意線段\( \overline{\mathrm{PQ}} \)。取不在其上的任意一點\( \mathrm{R} \)。過\( \mathrm{R} \),畫\( \overline{\mathrm{PQ}} \) 的垂線。(使用尺子和三角板)
- 如果 A 和 B 的點為 (-2, -2) 和 (2, -4),而 P 是位於 AB 上的點,使得 AP = $\frac{3}{7}$ AB,則求 P 的座標。
- 兩條切線段\( P A \) 和\( P B \) 被畫到一個以\( O \) 為中心的圓上,使得\( \angle A P B=120^{\circ} . \) 證明\( O P=2 A P \)。
- 在每種情況下畫一個草圖並適當地標記:(a) 點\( P \) 位於\( \overline{\mathrm{AB}} \) 上。(b) \( \overline{\mathrm{XY}} \) 和\( \overline{\mathrm{PQ}} \) 相交於\( \mathrm{M} \)。(c) 直線\( l \) 包含\( \bar{E} \) 和\( \bar{F} \) 但不包含\( \bar{D} \)。(d) \( \overline{\mathrm{OP}} \) 和\( \overline{\mathrm{OQ}} \) 相交於\( O \)。
- 將 $0.\overline{3}$ 轉換為 $\frac{p}{q}$ 形式。
- 指出下列哪些是三角形。\( \overline{A B}=7 \mathrm{~cm}, \overline{B C}=8 \mathrm{~cm}, \quad \overline{A C}=7 \mathrm{~cm} \)
- 點 P 將連線點 $A( 3,\ -5) $ 和 $B( -4,\ 8)$ 的線段分成兩部分,使得 $\frac{AP}{PB} =\frac{K}{1}$ 。如果 P 位於直線 $x+y=0$ 上,則求 K 的值。
- 點 $P$ 將連線點 $A (3, -5)$ 和 $B (-4, 8)$ 的線段分成兩部分,使得 $\frac{AP}{PB} = \frac{k}{1}$。如果 $P$ 位於直線 $x + y = 0$ 上,則求 $k$ 的值。
- 課堂活動(構建“平方根螺旋”):取一張大紙,按照以下方式構建“平方根螺旋”。從一個點\( \mathrm{O} \) 開始,畫一條長度為單位長度的線段\( \mathrm{OP}_{1} \)。畫一條垂直於\( \mathrm{OP}_{1} \) 的長度為單位長度的線段\( \mathrm{P}_{1} \mathrm{P}_{2} \)(見下圖)。現在畫一條垂直於\( \mathrm{OP}_{2} \) 的線段\( \mathrm{P}_{2} \mathrm{P}_{3} \)。然後畫一條垂直於\( \mathrm{OP}_{3} \) 的線段\( \mathrm{P}_{3} \mathrm{P}_{4} \)。以圖 1.9:構建這種方式繼續下去,您可以透過畫一條垂直於\( \mathrm{OP}_{\mathrm{n}-1} \) 的長度為單位長度的線段來獲得線段\( \mathrm{P}_{\mathrm{a}-1} \mathrm{P}_{\mathrm{n}} \)。透過這種方式,您將建立點\( \mathrm{P}_{2}, \mathrm{P}_{3}, \ldots, \mathrm{P}_{\mathrm{n}}, \ldots . \),並將它們連線起來以建立一個美麗的螺旋,描繪\( \sqrt{2}, \sqrt{3}, \sqrt{4}, \ldots \)"

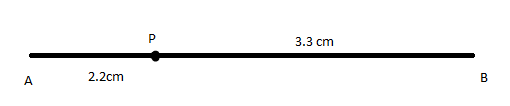


 資料結構
資料結構 網路
網路 RDBMS
RDBMS 作業系統
作業系統 Java
Java iOS
iOS HTML
HTML CSS
CSS Android
Android Python
Python C 語言程式設計
C 語言程式設計 C++
C++ C#
C# MongoDB
MongoDB MySQL
MySQL Javascript
Javascript PHP
PHP