資料結構
網路
關係資料庫管理系統 (RDBMS)
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C語言程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理
化學
生物
數學
英語
經濟學
心理學
社會學
時尚研究
法學研究畫一個以 \( O \) 為頂點的任意角。在角的兩條邊上分別取點 \( A \) 和 \( B \)，使得 \( \mathrm{OA}=\mathrm{OB} \)。作 \( \overline{\mathrm{OA}} \) 和 \( \overline{\mathrm{OB}} \) 的垂直平分線。設它們交於點 P。那麼 \( \mathrm{PA}=\mathrm{PB} \) 嗎？
待辦事項
我們必須畫出$\overline{OA}$和$\overline{OB}$的垂直平分線，設它們交於點$P$，並判斷$PA=PB$是否成立。
解答
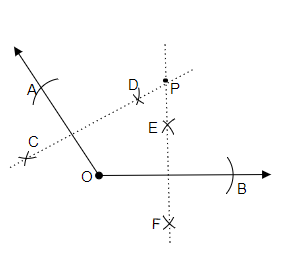
作圖步驟：
(i) 畫一個任意角，其頂點為$O$。
(ii) 使用圓規，以$O$為圓心，在角的一條邊上畫弧，並將弧與邊的交點命名為$A$。
(iii) 同樣地，使用圓規，以$O$為圓心，$OA$為半徑畫弧，在角的另一條邊上標出交點，命名為$B$。
(iv) 取大於$\overline{OA}$一半長度的距離，在$\overline{OA}$的上方和下方分別畫兩條弧，並將弧的交點標記為$C$和$D$。
(v) 同樣地，取大於$\overline{OB}$一半長度的距離，在$\overline{OB}$的上方和下方分別畫兩條弧，並將弧的交點標記為$E$和$F$。
(vi) 連線點$C$和$D$，得到$\overline{OA}$的垂直平分線。同樣地，連線點$E$和$F$，得到$\overline{OB}$的垂直平分線。
(vii) 延長這兩條垂直平分線，它們相交於一點，將該交點標記為$P$。
(viii) 測量$\overline{PA}$和$\overline{PB}$的長度，它們相等。因此，$\overline{PA}= \overline{PB}$。
更新於：2022年10月10日
45 次瀏覽
廣告