電阻的電路連線

---

---

當電阻連線到電路中時，該連線可以是串聯或並聯。現在讓我們瞭解一下，如果它們串聯連線以及並聯連線時，總電流、電壓和電阻值將發生什麼變化。

串聯電阻

讓我們觀察一下，當幾個電阻串聯連線時會發生什麼。讓我們考慮三個不同值的電阻，如下圖所示。

電阻

具有串聯電阻的電路的總電阻等於各個電阻的總和。這意味著，在上圖中，有三個電阻，其值分別為 1KΩ、5KΩ 和 9KΩ。

電阻網路的總電阻值為 -

$$R\:\:=\:\:R_{1}\:+\:R_{2}\:+\:R_{3}$$

這意味著 1 + 5 + 9 = 15KΩ 是總電阻。

其中 R₁ 是第一個電阻的電阻，R₂ 是第二個電阻的電阻，R₃ 是上述電阻網路中第三個電阻的電阻。

電壓

出現在串聯電阻網路兩端的總電壓是每個電阻電壓降的總和。在上圖中，我們有三個不同的電阻，每個階段都有三個不同的電壓降值。

出現在電路兩端的總電壓 -

$$V\:\:=\:\:V_{1}\:+\:V_{2}\:+\:V_{3}$$

這意味著 1v + 5v + 9v = 15v 是總電壓。

其中 V₁ 是第一個電阻的電壓降，V₂ 是第二個電阻的電壓降，V₃ 是上述電阻網路中第三個電阻的電壓降。

電流

流過一組串聯連線的電阻的總電流在整個電阻網路中的所有點都相同。因此，在輸入端或電阻之間的任何點，甚至在輸出端測量時，電流都相同，為 5A。

透過網路的電流 -

$$I\:\:=\:\:I_{1}\:=\:I_{2}\:=\:I_{3}$$

這意味著所有點的電流都是 5A。

其中 I₁ 是流過第一個電阻的電流，I₂ 是流過第二個電阻的電流，I₃ 是上述電阻網路中流過第三個電阻的電流。

並聯電阻

讓我們觀察一下，當幾個電阻並聯連線時會發生什麼。讓我們考慮三個不同值的電阻，如下圖所示。

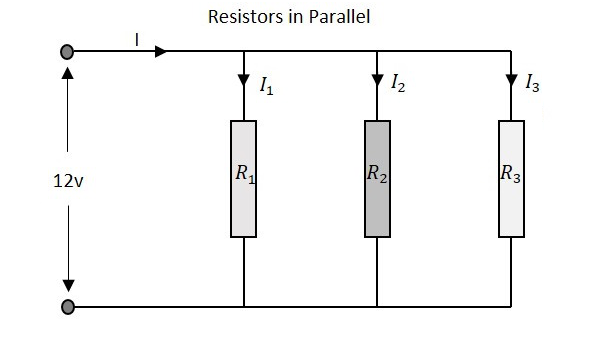
電阻

具有並聯電阻的電路的總電阻的計算方法與串聯電阻網路方法不同。在這裡，將各個電阻的倒數 (1/R) 值與代數和的倒數相加，以獲得總電阻值。

電阻網路的總電阻值為 -

$$\frac{1}{R}\:\:=\:\:\frac{1}{R_{1}}\:\:+\:\:\frac{1}{R_{2}}\:\:+\frac{1}{R_{3}}$$

其中 R₁ 是第一個電阻的電阻，R₂ 是第二個電阻的電阻，R₃ 是上述電阻網路中第三個電阻的電阻。

例如，如果考慮前面示例中的電阻值，這意味著 R₁ = 1KΩ，R₂ = 5KΩ 和 R₃ = 9KΩ。並聯電阻網路的總電阻將為 -

$$\frac{1}{R}\:\:=\:\:\frac{1}{1}\:\:+\:\:\frac{1}{5}\:\:+\frac{1}{9}$$

$$=\:\:\frac{45\:\:+\:\:9\:\:+\:\:5}{45}\:\:=\:\:\frac{59}{45}$$

$$R\:\:=\:\:\frac{45}{59}\:\:=\:\:0.762K\Omega\:\:=\:\:76.2\Omega$$

根據我們計算並聯電阻的方法，我們可以推匯出一個用於雙電阻並聯網路的簡單方程。它是 -

$$R\:\:=\:\:\frac{R_{1}\:\:\times\:\:R_{2}}{R_{1}\:\:+\:\:R_{2}}\:$$

電壓

出現在並聯電阻網路兩端的總電壓與每個電阻的電壓降相同。

出現在電路兩端的電壓 -

$$V\:\:=\:\:V_{1}\:=\:V_{2}\:=\:V_{3}$$

其中 V₁ 是第一個電阻的電壓降，V₂ 是第二個電阻的電壓降，V₃ 是上述電阻網路中第三個電阻的電壓降。因此，電壓在並聯電阻網路的所有點都相同。

電流

進入並聯電阻網路的總電流是所有並聯支路中流過的所有各個電流的總和。每個支路的電阻值決定了流過它的電流值。透過網路的總電流為

$$I\:\:=\:\:I_{1}\:+\:I_{2}\:+\:I_{3}$$

其中 I₁ 是流過第一個電阻的電流，I₂ 是流過第二個電阻的電流，I₃ 是上述電阻網路中流過第三個電阻的電流。因此，不同支路中各個電流的總和得到並聯電阻網路中的總電流。

電阻通常用作許多電路輸出端的負載。如果根本不使用電阻負載，則在負載前放置一個電阻。電阻通常是任何電路中的基本元件。