資料結構
網路
RDBMS
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 語言程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理學
化學
生物學
數學
英語
經濟學
心理學
社會學
時尚研究
法律研究Swift 程式，用於求解已知兩邊長 l 和 b 的直角三角形的斜邊長度
本教程將討論如何編寫一個 Swift 程式來求解已知兩邊長 l 和 b 的直角三角形的斜邊長度。
如果一個三角形中有一個角等於 90 度，並且另外兩個角的和也等於 90 度，那麼這種型別的三角形被稱為直角三角形。直角三角形有三條邊：底邊、高和斜邊。我們可以使用勾股定理來找到這三條邊之間的關係。
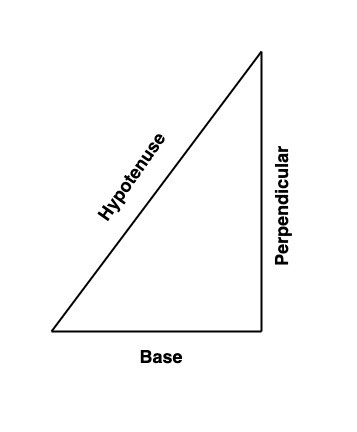
在直角三角形中，斜邊（也稱為三角形中最長的一邊）的平方等於其他兩邊的平方和，這就是勾股定理。
公式
以下是斜邊的公式：
(hypotenuse)2 = (perpendicular)2 + (Base)2 Or H = √(l)2 + (b)2
下面是同一個公式的演示：
輸入
假設我們給定的輸入是：
l = 6 b = 8
輸出
期望的輸出將是：
H = 10
演算法
以下是演算法：
步驟 1 - 宣告兩個變數，名為“triPerpendicular”和“triBase”，並賦予使用者定義/預定義的值。
步驟 2 - 宣告另一個名為“triHypotenuse”的變數。它儲存從以下公式推匯出的斜邊值
var triHypotenuse = Int(sqrt(pow(triPerpendicular, 2) + pow(triBase, 2)))
步驟 3 - 列印輸出
示例 1
以下程式演示瞭如何求解已知兩邊長 l 和 b 的直角三角形的斜邊長度。
import Foundation import Glibc var triPerpendicular = 8.0 var triBase = 10.0 // Finding the hypotenuse of the right-angled triangle var triHypotenuse = Int(sqrt(pow(triPerpendicular, 2) + pow(triBase, 2))) print("Perpendicular - ", triPerpendicular) print("Base - ", triBase) print("Hypotenuse - ", triHypotenuse)
輸出
Perpendicular - 8.0 Base - 10.0 Hypotenuse - 12
在這裡，在上面的程式碼中，我們使用勾股定理求解直角三角形的斜邊：
var triHypotenuse = Int(sqrt(pow(triPerpendicular, 2) + pow(triBase, 2)))
在這裡，我們使用 pow() 函式求高和底邊的平方，然後使用 sqrt() 函式求高和底邊平方和的平方根，並使用 Int() 函式將浮點數結果轉換為整數。給定高 = 8.0 和底邊 = 10.0，所以斜邊 = 12。
示例 2
以下程式演示瞭如何求解已知兩邊長 l 和 b 的直角三角形的斜邊長度。
import Foundation import Glibc // Taking input from the user print("Please enter the sides of right-angled triangle") print("Enter the value of Perpendicular:") var triPerpendicular = Double(readLine()!)! print("Enter the value of base:") var triBase = Double(readLine()!)! // Finding the hypotenuse of the right-angled triangle var triHypotenuse = Int(sqrt(pow(triPerpendicular, 2) + pow(triBase, 2))) print("Perpendicular - ", triPerpendicular) print("Base - ", triBase) print("Hypotenuse - ", triHypotenuse)
標準輸入
Please enter the sides of right-angled triangle Enter the value of Perpendicular: 6 Enter the value of base: 8
輸出
Perpendicular - 6.0 Base - 8.0 Hypotenuse - 10
在這裡，在上面的程式碼中，我們使用勾股定理求解直角三角形的斜邊：
var triHypotenuse = Int(sqrt(pow(triPerpendicular, 2) + pow(triBase, 2)))
在這裡，我們使用 pow() 函式求高和底邊的平方，然後使用 sqrt() 函式求高和底邊平方和的平方根，並使用 Int() 函式將浮點數結果轉換為整數。這裡，高和底邊的值由使用者給出。因此，使用者輸入高 = 6.0 和底邊 = 8.0，所以斜邊 = 10。
更新於： 2022-08-25
325 次瀏覽
廣告