使用與非門實現全減器

---

在數位電子技術中，減法器是一種組合邏輯電路，用於執行兩個二進位制數的減法運算。然而，二進位制數的減法可以透過採用1的補碼或2的補碼的方法，使用加法器電路來實現。但是，我們也可以實現一個專門的電路來執行兩個二進位制數的減法。

在兩個二進位制數的減法中，被減數的每個位都減去其對應位的減數位，以形成差位。在減法過程中，如果被減數位小於減數位，則從下一位借位1。根據輸入位的數量，減法器有兩種型別，即半減器和全減器。

半減器是一種接收兩個二進位制數作為輸入，並輸出差位和借位（如果有）的電路。另一方面，全減器是一種接收三個位作為輸入的電路，即兩個輸入位和一個來自前一級的輸入借位，並輸出差位和輸出借位。

由於減法器是一種組合邏輯電路，即它是由邏輯閘組成的。我們可以使用不同型別的邏輯閘（如與門、或門、非門、與非門、或非門等）來實現全加器電路。在本文中，我們將討論使用與非門實現全減器。但在那之前，讓我們先了解一下全減器的基礎知識。

什麼是全減器？

全減器是一種組合電路，具有三個輸入 A、B、bin 和兩個輸出 d 和 b。其中，A 是被減數，B 是減數，bin 是前一級的借位，d 是差輸出，b 是借位輸出。全減器的框圖如圖1所示。

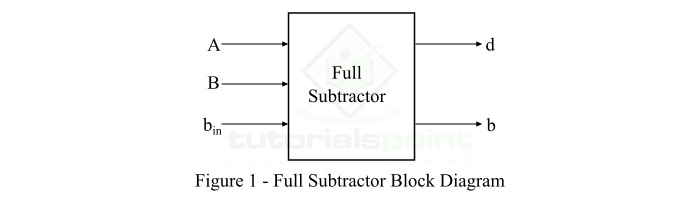
全減器的真值表

以下是全減器的真值表：

輸入			輸出
A	B	bin	d（差）	b（借位）
0	0	0	0	0
0	0	1	1	1
0	1	0	1	1
0	1	1	0	1
1	0	0	1	0
1	0	1	0	0
1	1	0	0	0
1	1	1	1	1

從此表中，我們可以確定差位 (d) 和借位輸出 (b) 的方程。這些方程如下：

全減器的差 (d) 為：

$$\mathrm{Difference,\, d=A'B'b_{in}+AB'b'_{in}+A'Bb'_{in}+ABb_{in}=A\oplus B\oplus b_{in}}$$

全減器的輸出借位 (b) 由下式給出：

$$\mathrm{Borrow,\, b=A'B'b_{in}+A'Bb'_{in}+A'Bb_{in}+ABb_{in}}$$

現在，讓我們討論一下使用與非門實現全減器。

使用與非門實現全減器

我們可以僅使用與非門來實現全減器電路，如圖2所示。

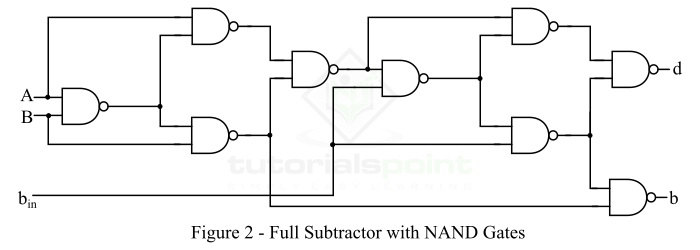
從使用與非邏輯實現的全減器的邏輯電路中，我們可以看到，在與非邏輯中實現全減器需要9個與非門。

全減器在與非邏輯中的差位 (d) 和輸出借位 (b) 的輸出方程如下：

差位 (d)

$$\mathrm{Difference,\, d=\overline{\overline{(A\oplus B)\cdot \overline{(A\oplus B)b_{in}}}\cdot \overline{b_{in}\cdot \overline{(A\oplus B)b_{in}}}}=A\oplus B\oplus b_{in}}$$

其中，

$$\mathrm{A\oplus B=\overline{\overline{A \cdot\overline{AB}}\cdot \overline{B \cdot\overline{AB}}}}$$

借位 (b)

$$\mathrm{Borrow,\, b=\overline{\overline{B \cdot\overline{AB}}\cdot \overline{b_{in} \overline{[b_{in}\cdot (A\oplus B)]}}}=\overline{A}B+b_{in}(\overline{A\oplus B})}$$

這樣，我們就可以僅使用與非門來實現全減器。