象限

---

引言

笛卡爾平面是一個二維平面，它是座標系的一部分。笛卡爾平面的概念主要用於歐幾里得幾何和代數。在二維平面系統中，任何點都可以由x座標和y座標指定。笛卡爾平面上的軸線將其劃分為4個相等且無限的部分，稱為象限。這些象限分別命名為第一象限、第二象限、第三象限和第四象限。在圓的情況下，象限可以用圓的四分之一來表示。因此，讓我們簡要研究笛卡爾平面和圓的象限主題。

笛卡爾平面

笛卡爾平面可以定義為由兩個相互垂直的座標軸相交形成的平面。水平軸是x軸，垂直軸稱為y軸。x軸和y軸相交於一點，稱為原點，用符號O表示。

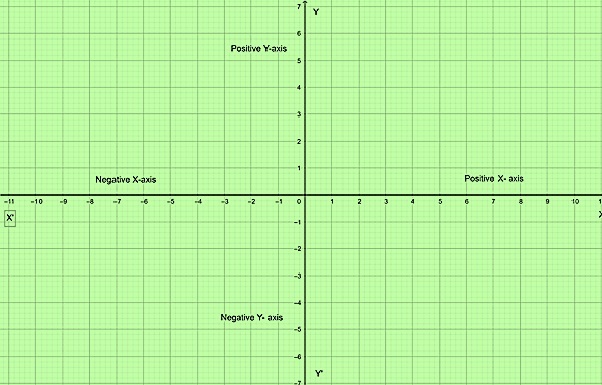
帶有正負x軸和y軸的笛卡爾平面

笛卡爾平面的組成部分

笛卡爾平面具有三個主要組成部分：**軸、原點**和**象限**。當我們要在笛卡爾平面上定位任何點時，這些組成部分是必不可少的。笛卡爾平面的組成部分如下所示

軸

笛卡爾平面上的水平線和垂直線稱為軸。水平軸稱為x軸，垂直軸稱為y軸。

原點

兩條軸相交的點稱為原點。它用O表示。原點的座標為(0,0)。

象限

當x軸和y軸相互垂直時，它們將笛卡爾平面分成4個相等的部分。這些部分稱為**象限**。

笛卡爾平面的象限

當x軸和y軸相互交叉時，它們將笛卡爾平面分成4個相等且無限的部分。這些部分稱為象限。這些象限分別表示為第一象限、第二象限、第三象限和第四象限。

第一象限

第一象限位於笛卡爾平面的右上角。在這個象限中，x座標和y座標都是正數。

第二象限

第二象限位於笛卡爾平面的左上角。在這個象限中，x座標為負數，y座標為正數。

第三象限

第三象限位於笛卡爾平面的左下角。在這個象限中，x座標和y座標都是負數。

第四象限

第四象限位於笛卡爾平面的右下角。在這個象限中，x座標為正數，y座標為負數。

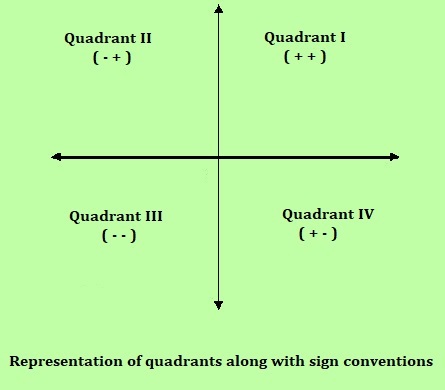
笛卡爾平面中象限的性質

• x軸的右側被認為是正數，x軸的左側被認為是負數。

• 類似地，上y軸被認為是正數，下y軸被認為是負數。

• 象限和負軸以及正軸在繪製圖形中起著重要作用。

• x的值稱為x座標或橫座標。它表示該點到y軸的距離。

• 類似地，y的值稱為y座標或縱座標。它表示該點到x軸的距離。

圓

在笛卡爾平面上，圓是在平面內運動的點的軌跡，保持與平面內給定固定點之間的距離恆定。

圓的象限

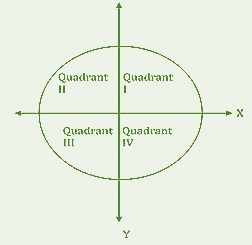
象限是笛卡爾系統中的四個四分之一。每個部分稱為象限。在圓的情況下，圓的四分之一稱為象限。圓的每個四分之一測量90⁰。這四個四分之一加起來共計360⁰。當我們連線這個象限時，我們會得到一個圓的形狀。象限分別命名為第一象限、第二象限、第三象限和第四象限，如上圖所示。

圓形象限的不同公式

• 象限面積 =$\mathrm{\frac{1}{4}×πr^2}$

• 象限圓周 =$\mathrm{\frac{1}{4}×2πr}$

• 象限周長 =$\mathrm{\frac{πr}{2}+2r}$

(注意：計算周長時，應將整個邊界加上圓形邊界的兩倍半徑。因為象限由兩個圓形部分和兩條直線組成，其長度等於半徑。)

例如，求半徑為10m的圓的象限面積。假設π=3.141。

解 計算象限面積的公式為：

這裡，r=10，π=3.141

$$\mathrm{A=\frac{πr^2}{4}=\frac{3.141×(10)^2}{4}=78.525m^2.}$$

例2 求半徑為11cm的圓的象限周長。

解：這裡，r= 11 cm，計算象限周長的公式為：

$$\mathrm{P=11×\frac{3.141}{2}+2=19.276 cm}$$

圓的象限的性質

• 第一象限是圓的右上角部分。在這個象限中，x座標和y座標都是正數。象限中的角度範圍從0⁰到90⁰。

• 第二象限是圓的左上角部分。在這個象限中，x座標為負數，y座標為正數。象限中的角度範圍從90⁰到180⁰。

• 第三象限是圓的左下角部分。在這個象限中，x座標和y座標都是負數。象限中的角度範圍從180⁰到270⁰。

• 第四象限是圓的右下角部分。在這個象限中，x座標為正數，y座標為負數。象限中的角度範圍從270⁰到360⁰。

結論

本教程涵蓋了笛卡爾平面、笛卡爾平面中的象限、圓和圓的象限及其性質等主題。

常見問題

1. 笛卡爾平面的一些應用是什麼？

笛卡爾平面用於確定兩點之間的距離、兩條分割線的比率以及相交線的中間點。

2. (2, -3) 是否位於第四象限？

是的。(2, -3) 位於第四象限。因為x的值為正，y的值為負。因此，該點應該位於第四象限。

3. 第三象限是正數還是負數？

不是。第三象限中的x座標和y座標都是負數。

4. 什麼是單位圓？

單位圓是一個半徑為一個單位的圓。這個圓大多在笛卡爾和座標平面上表示。這個圓有助於尋找三角比率的值。

5. 圓的象限和扇區有什麼區別？

象限是圓的四分之一，角度為90⁰。扇區是圓的任何角度的劃分。