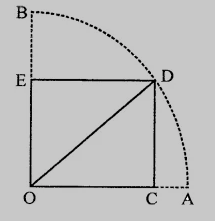
如圖所示，矩形$OCDE$內接於半徑為$10\ cm$的圓的四分之一圓弧中。如果$OE = 2\sqrt5$，求矩形的面積。
"\n

已知

矩形$OCDE$內接於半徑為$10\ cm$的圓的四分之一圓弧中。

$OE = 2\sqrt5$。

要求

我們需要求出矩形的面積。

解答

圓的四分之一圓弧的半徑$= 2\sqrt5$ 個單位

矩形的對角線 = 10 個單位          ($OD = OB = OA = 10\ cm$)

$DE = 2\sqrt5\ cm$

在$\triangle OED$中，

$OD^2 = OE^2 + DE^2$

$10^2 = OE^2 + (2\sqrt5)^2$

$100 = OE^2 + 20$

$OE^2 = 100 - 20$

$ = 80$

$OE^2 = (4\sqrt5)^2$

$\Rightarrow OE = 4\sqrt5\ cm$

矩形的面積 $= l \times b$

$= DE \times OE$

$= 2\sqrt5 \times 4\sqrt5$

$= 8 \times 5$

$= 40\ cm^2$

矩形的面積為$40\ cm^2$。

教程點

更新於: 2022年10月10日

51 次瀏覽

開啟你的職業生涯

透過完成課程獲得認證

開始學習