資料結構
網路
關係型資料庫管理系統
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 語言程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理學
化學
生物學
數學
英語
經濟學
心理學
社會學
服裝設計
法律一條跑道的內周長為 \( 400 \mathrm{~m} \)。每段直線的長度為 \( 90 \mathrm{~m} \)，兩端為半圓形。如果跑道處處寬 14 \( m \)，求跑道的面積。另外，求外跑道的長度。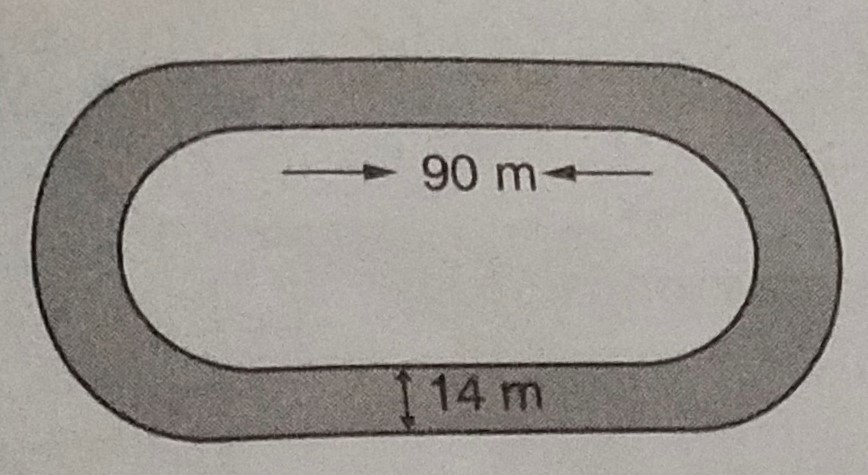
"\n
已知：
跑道的內周長為 \( 400 \mathrm{~m} \)。
每段直線的長度為 \( 90 \mathrm{~m} \)，兩端為半圓形。
跑道處處寬 14 \( m \)。
要求：
我們需要求出跑道的面積和外跑道的長度。
解答
每個半圓形的周長 $=\frac{400-(90+90)}{2}$
$=\frac{400-180}{2}$
$=\frac{220}{2}$
$=110 \mathrm{~m}$
設內半圓的半徑為 $r$。
這意味著，
$\frac{1}{2} \times 2 \pi r=110$
$\Rightarrow \frac{22}{7} r=110$
$\Rightarrow r=\frac{110 \times 7}{22}$
$\Rightarrow r=35 \mathrm{~m}$
跑道的寬度 $=14 \mathrm{~m}$
這意味著，
跑道的外部半徑 $r=35+14$
$=49 \mathrm{~m}$
兩個半圓形的外周長 $=2 \pi \mathrm{R}$
$=2 \times \frac{22}{7} \times 49$
$=308 \mathrm{~m}$
因此，
跑道的總周長 $=308+90+90 \mathrm{~m}$
$=488 \mathrm{~m}$
跑道的面積 $=2 \times 90 \times 14 +2 \times \frac{1}{2}(\pi \mathrm{R}^{2}-\pi r^{2})$
$=2520+\pi(49^{2}-35^{2})$
$=2520+\frac{22}{7}(49+35)(49-35)$
$=2520+\frac{22}{7} \times 84 \times 14$
$=2520+3696$
$=6216 \mathrm{~m}^{2}$
跑道的面積為 $6216\ m^2$，外跑道的長度為 $49\ m$。
25 次瀏覽
