在給定圖形中，檢查是否 $x+y=p+q$。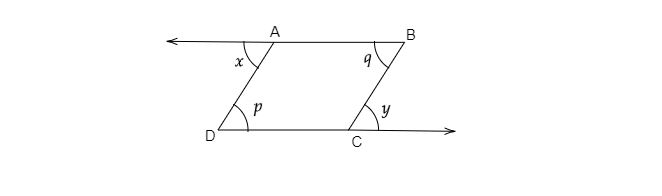
"\n
已知：在給定圖形中，兩條橫截線與兩條平行線 $AB$ 和 $CD$ 相交。
要求：檢查是否 $x+y=p+q$。
解答
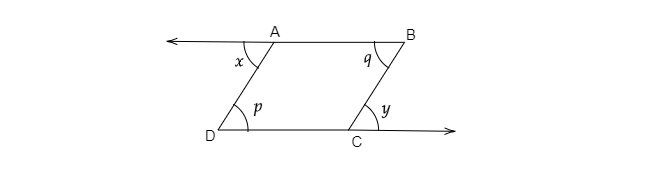
如我們所知，當一條橫截線與兩條平行線相交時，內錯角相等。
$\Rightarrow \angle x=\angle p\ ......\ ( i)$
同樣地，$\angle y=\angle q\ .....\ ( ii)$
將 $( i)$ 和 $( ii)$ 相加，
$\angle x+ \angle y=\angle x+\angle y$
- 相關文章
- 在 \( \Delta X Y Z, X Y=X Z \) 中，一條直線與 \( X Z \) 交於 \( P \)，與 \( Y Z \) 交於 \( Q \)，與 \( X Y \) 的延長線交於 \( R \)。如果 \( Y Q=Y R \) 且 \( Q P=Q Z \)，求 \( \Delta X Y Z \) 的角。
- 在圖中，\( O Q: P Q=3: 4 \) 且 \( \Delta P O Q \) 的周長為 \( 60 \mathrm{~cm} \)。確定 \( P Q, Q R \) 和 \( O P \)。"\n
- 如果 p、q 為實數且 p≠q，則證明方程 $(p-q)x^2+5(p+q)x-2(p-q)=0$ 的根為實數且不相等。
- 在給定圖形中，求 \( x \)。"\n
- 對於以下方程組，求 \( p \) 和 \( q \) 的值：\( 2 x+3 y=7 \) 和 \( 2 p x+p y=28-q y \)，如果方程組有無數個解。
- 從下面給出的選項中，選擇圖形中給出的方程。$y = x$$x + y = 0$$y = 2x$$2 + 3y = 7x$"\n
- 解下列線性方程組：(i) \( p x+q y=p-q \)$q x-p y=p+q$(ii) \( a x+b y=c \)$b x+a y=1+c$,b>(iii) \( \frac{x}{a}-\frac{y}{b}=0 \)$a x+b y=a^{2}+b^{2}$(iv) \( (a-b) x+(a+b) y=a^{2}-2 a b-b^{2} \)$(a+b)(x+y)=a^{2}+b^{2}$(v) \( 152 x-378 y=-74 \)$-378 x+152 y=-604$.
- \( N \) 是一個正整數，\( p \) 和 \( q \) 是素數。如果 \( N=p q \) 且 \( \frac{1}{N}+\frac{1}{p}=\frac{1}{q}, \) 則求 \( N \) 的值。
- 如果點 $P, Q (x, 7), R, S (6, y)$ 按此順序將連線 $A (2, p)$ 和 $B (7,10)$ 的線段分成 5 等份，求 $x, y$ 和 $p$。
- 在三角形 \( P Q R \) 中，\( N \) 是 \( P R \) 上的一點，使得 \( Q N \perp P R \)。如果 \( P N \). \( N R=Q^{2} \)，證明 \( \angle \mathrm{PQR}=90^{\circ} \)。
- 在圖中，P 是 AB 的中點，PQ ∥ BC。求 x 和 y。"\n
- 一些多項式 \( p(x) \) 的 \( y=p(x) \) 影像如下圖 2.10 所示。在每種情況下，求 \( p(\bar{x}) \) 的零點個數。"\n
- 在給定圖形中，求 \( x \) 的值。"\n
- 確定給定圖形中 $x$ 的值。"\n
- 在給定圖形中，$PR>PQ$ 且 PS 平分 $\angle QPR$。證明 \( \angle P S R>\angle P S Q \)。"\n
開啟你的 職業生涯
透過完成課程獲得認證
開始學習
資料結構
網路
關係型資料庫管理系統
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 語言程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理學
化學
生物學
數學
英語
經濟學
心理學
社會學
時尚研究
法律研究