如圖所示，PQRS是一個正方形，SRT是一個等邊三角形。證明∠TQR = 15°。

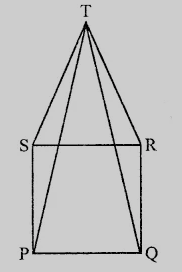
已知

PQRS是一個正方形，SRT是一個等邊三角形。

要求

我們必須證明PT = QT。

解答

在△TSP和△TQR中，

ST = RT (等邊三角形的邊)

SP = PQ (正方形的邊)

∠TSP = ∠TRQ

因此，根據SAS公理，

△TSP ≅ △TQR

這意味著，

PT = QT (全等三角形對應邊相等)

在△TQR中，

RT = RQ (正方形的邊)

∠RTQ = ∠RQT

∠TRQ = 60° + 90° = 150°

∠RTQ + ∠RQT = 180° - 150° = 30°

∠PTQ = ∠RQT

這意味著，

∠RQT = 30°/2 = 15°

∠TQR = 15°

證畢。

Tutorialspoint

更新於：2022年10月10日

40次瀏覽

開啟您的職業生涯

完成課程獲得認證

開始學習