資料結構
網路
關係型資料庫管理系統
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 語言程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理
化學
生物
數學
英語
經濟學
心理學
社會學
時尚研究
法律研究$PQRS$ 是一個矩形。如果已知 $\angle QOR$，求 $\angle OPS$。$( a).\ 42^o$ $( b).\ 56^o$.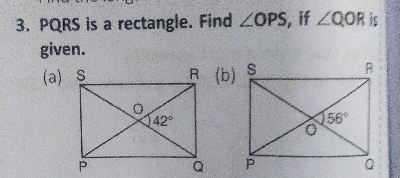
"\n
已知：$PQRS$ 是一個矩形。
求解：如果 $\angle QOR$ 為：$( a).\ 42^o$ $( b).\ 56^o$，求 $\angle OPS$。
解題步驟
$( a).\ \because PQRS$ 是一個矩形，因此對角線 $PR$ 和 $QS$ 等長。
$\therefore \frac{1}{2}PR=\frac{1}{2}QS$
$\Rightarrow OS=OP\ .......\ ( i)$
在 $\vartriangle OPS$ 中
$\angle POS=\angle QOR=42^o$ [已知]
$\angle OSP=\angle OPS$ [$\because OS=OP$]
$\therefore \angle POS+\angle OPS+\angle OPS=180^o$
$\Rightarrow 42^o+2\angle OPS=180^o$
$\Rightarrow 2\angle OPS=180^-42^o$
$\Rightarrow 2\angle OPS=138^o$
$\Rightarrow \angle OPS=\frac{138^o}{2}$
$\Rightarrow \angle OPS=69^o$
$( b)$ 同理，當 $\angle QOR=56^o$ 時
$\Rightarrow 2\angle OPS=180^o-56^o$
$\Rightarrow 2\angle OPS=124^o$
$\Rightarrow \angle OPS=\frac{124^o}{2}$
$\Rightarrow \angle OPS=62^o$
更新於： 2022年10月10日
370 次瀏覽
廣告