資料結構
網路
關係型資料庫管理系統
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理
化學
生物
數學
英語
經濟學
心理學
社會學
時尚研究
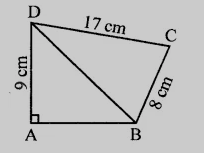
法律研究在圖中，計算四邊形的面積。
"\n
已知
在四邊形 $ABCD$ 中，
$\angle A = 90^o, \angle CBD = 90^o, AD = 9\ cm, BC = 8\ cm$ 和 $CD = 17\ cm$
要求
我們必須計算四邊形的面積。
解答
在 $\triangle BCD$ 中，
$CD^2 = BC^2 + BD^2$ (勾股定理)
$17^2 = 8^2 + BD^2$
$289 = 64 + BD^2$
$BD^2 = 289 - 64$
$= 225$
$= (15)^2$
$\Rightarrow BD = 15\ cm$
在 $\triangle ABD$ 中，
$BD^2 = AB^2 + AD^2$
$(15)^2 = AB^2 + (9)^2$
$225 = AB^2 + 81$
$AB^2= 225 - 81$
$= 144$
$= (12)^2$
$\Rightarrow AB = 12\ cm$
$\triangle \mathrm{ABD}$ 的面積$=\frac{1}{2}\times$ 底 $\times$ 高
$=\frac{1}{2} \mathrm{AB} \times \mathrm{AD}$
$=\frac{1}{2} \times 12 \times 9$
$=54 \mathrm{~cm}^{2}$
$\Delta \mathrm{BCD}$ 的面積$=\frac{1}{2} \times 8 \times 15$
$=60 \mathrm{~cm}^{2}$
因此，
四邊形 $\mathrm{ABCD}$ 的總面積$=54+60$
$=144 \mathrm{~cm}^{2}$.
更新於: 2022年10月10日
29 次瀏覽
廣告